This post is a noob-friendly introduction to whiteboxes along with the presentation and explanation of a (not-new) collision-based attack. The attack is demonstrated against a public whitebox, using QBDI to instrument and analyze the target in order to produce traces of execution.
Introduction, and purpose of this post
Disclaimer
This post is made to be an introduction to the field of whiteboxes. It is addressed to readers who have no previous experience analyzing such systems. We try to guide the reader from zero knowledge about the topic up to breaking a whitebox, using our tool [QBDI]. This without head-scratching maths or hundreds lines of code, so don't expect groundbreaking techniques or elite novelties :).
Why this post?
Whiteboxes may seem like a hard-to-reach subject, through this post we want to keep things simple both on the engineering side (because I can’t code), and the cryptographic side (because I can’t do maths and can’t write Mordor language). So, if like me you can’t do those, this post should be a great introduction!
In order to do so, in a first part we will talk about whiteboxes and concepts around them. Why they exist, use-cases and an introductory explanation based on whiteboxing the AES algorithm.
Whiteboxes are made to be broken, we will thus in the second part dig into a simple-to-understand (I believe) attack. By figuring out a few properties about AES, we will find a way to identify potential keys. We will then improve the identification process to distinguish the real key from all the potential ones.
Finally, we will study a public whitebox that we will break using the mentioned attack, based on traces generated thanks to QBDI.
Note: There are also a few resources that I recommend reading if you want to dig further [1] [2] [3] (and for French readers [4])
Whiteboxes: why and how?
Why whiteboxes?
To explain the need of whiteboxes, I will take the case of [DRM] (Digital Rights Management) protections for media content. You are basically in a case where you need to send a media to a client. This client should be able to play the media in the provided player and that is all. He should not be able to dump the data, play it from another device, etc.
This is something really hard to do, because - most of the time - the client has full control over the device, so you need to add all kinds of protections to prevent any pirate from accessing the raw content of the media.
To protect the content from “bad people”, various layers of protection are added (obfuscation, anti-debugs, code integrity, anti-lifting, cryptography...). The one of interest for us today is the cryptographic part.
Encryption restricts the access to the media to the sole users who have been granted the right permissions. It means the user is provided with a key to decrypt and play the DRM-ed content. This secret is really important and needs to be protected at all costs, because what would prevent somebody from sharing it with unauthorized users? That is the problem whitebox cryptography tries to address.
The goal is to hide the key from the user, but still let him use it to decrypt the data, so he can still watch the latest Marvel movie.
Note: In the case of a DRM-protected content, we would face a decryption algorithm, to recover the original data. For the rest of the article, we will however talk about encryption (both are similar in the way you would attack them).
Whiteboxed encryption VS standard encryption
So how does one hide the encryption key of an algorithm? Let’s take the [AES] algorithm (quite commonly whiteboxed) and have a look at what changes between a whiteboxed and a "clear" algorithm.
Reminders about AES
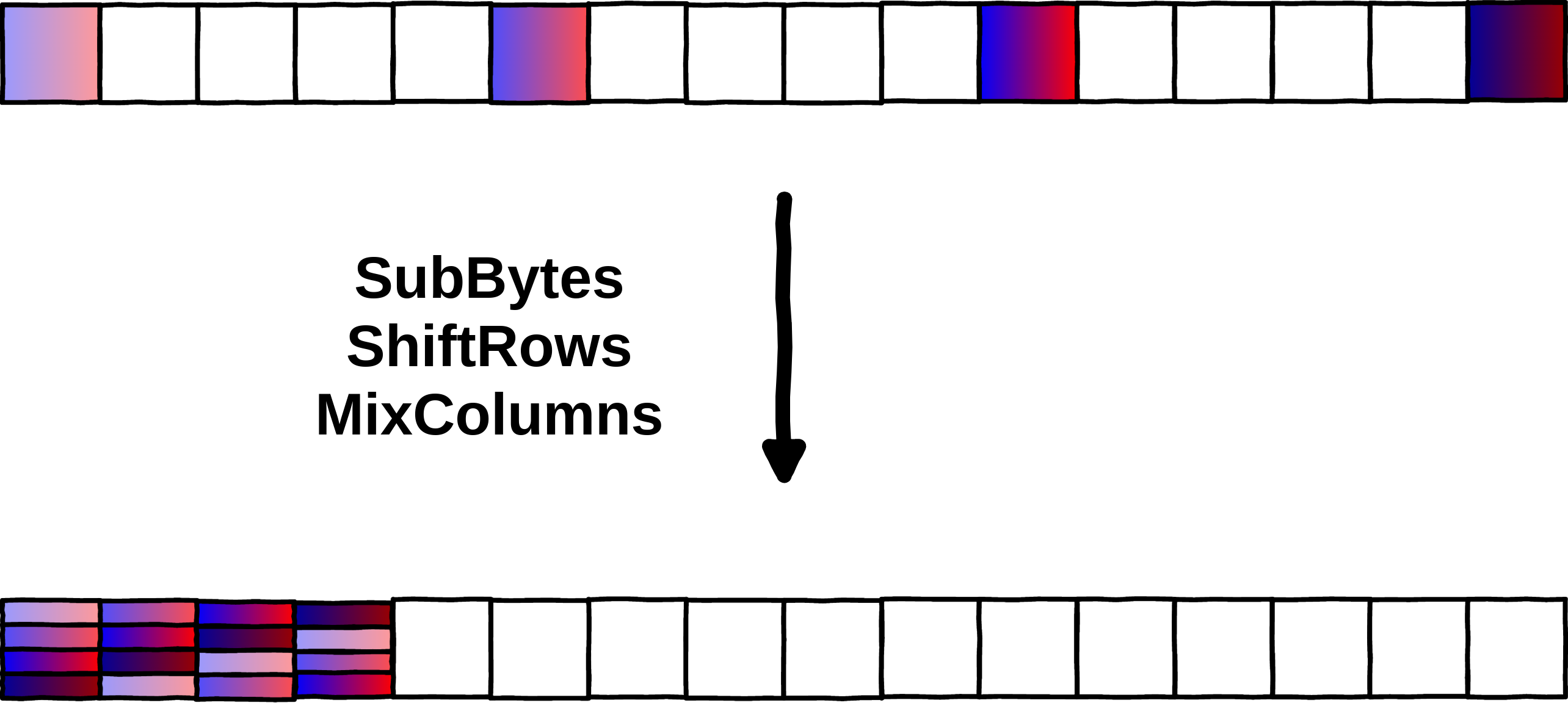
Quick reminder about AES, there are 3 variants based on the key length (128, 192 or 256 bits), and we will only look into AES-128 in this article. The mode of operation is not that important here because we will study the encryption of a single block of input (16 bytes). The encryption of a block is split in rounds (10, 12 or 14 rounds respectively, based on the key size) and is composed of 4 operations (the last round is a bit different but uses the same operations):
- AddRoundKey (the thing we want to protect in a whitebox context)
- SubstituteBytes
- ShiftRows
- MixColumns
Note: In this article, we consider that a round starts with AddRoundKey, and ends just before the next AddRoundKey. This is not an accurate definition of an AES round (see [AES_round]), but delimiting rounds that way will be easier for the sake of the explanations.
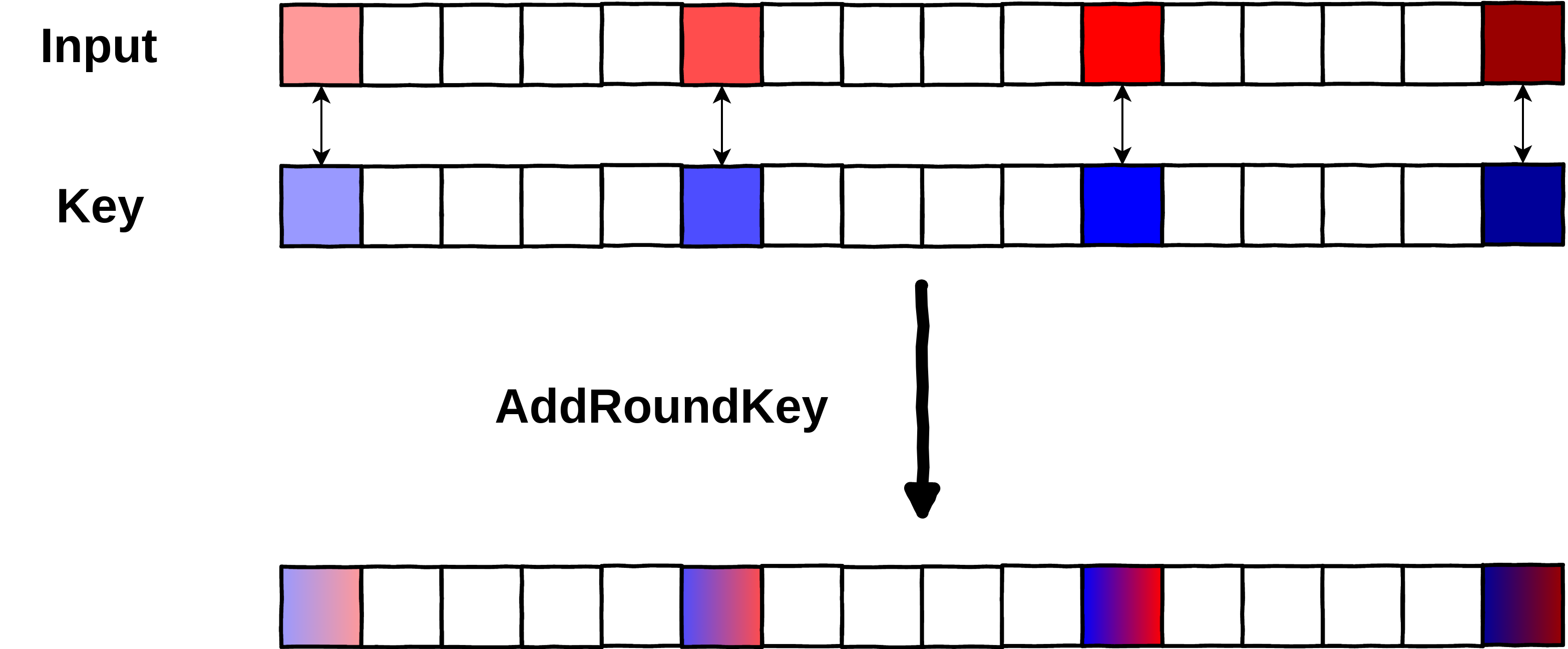
In an attacker-controlled environment, it would be pretty easy for a “bad guy” to retrieve the key. He could statically look for data used in the algorithm to find the key. In the case it was not stored in cleartext, he would just need to find that AddRoundKey operation (which is a simple XOR between the state and the round key) to retrieve a round key.
Note: Retrieving a single round key is game over, as you can recover the encryption key from any of them by reversing the key schedule. In the specific case of AES-128, the first round key is equal to the encryption key itself.
To avoid this, whitebox cryptography hides the key in such a way that, even with full inspection capabilities (memory, registers), the attacker cannot directly see it. This is achieved by merging together the various operations of AES into huge tables of precomputed data (along with the round keys that are precomputed instead of relying on the runtime computation of those during the key scheduling phase). With those precomputed tables, the encryption round-key never appears in clear (being in a register, or memory), making it a bit harder to recover it.
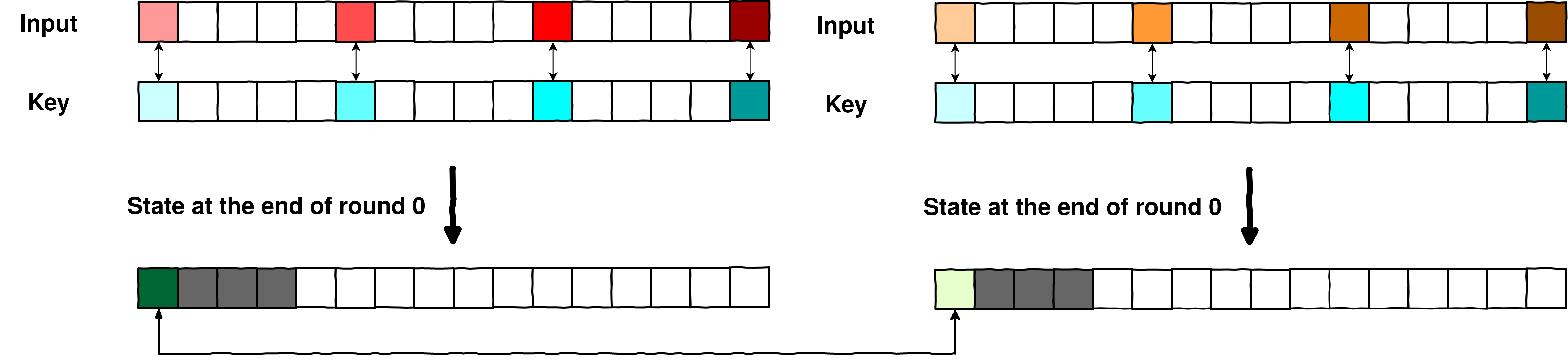
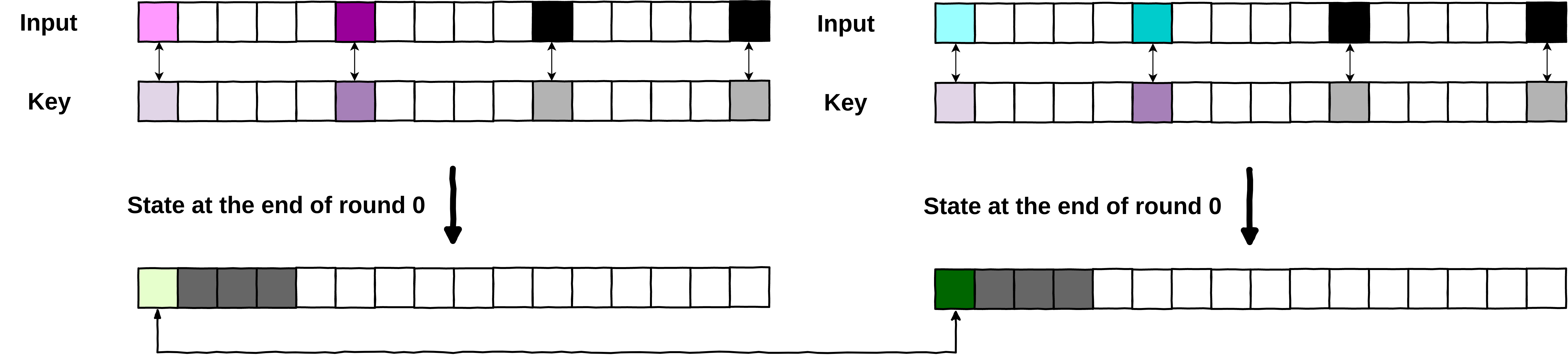
Below is an example of what an attacker could observe on the first round (round 0) of a clear AES and on the first round of a whiteboxed AES. We used [PhoenixAES] to easily visualize each of the operation of AES, even if that is not the main usage of the tool:
Note: this is a demo, there are no real precomputed tables, just a supposed observing attacker.
import phoenixAES def aes_round_0_whiteboxed(state): # Unknown implementation def aes_round_0(state): key = [1]*16 print("Original state\t", state) state=phoenixAES.AddKey(state, key) print("AddRoundKey\t", list(state)) state=phoenixAES.SBox(state) print("SubstituteBytes\t", list(state)) state=phoenixAES.ShiftRow(state) print("ShiftRows\t", list(state)) state=phoenixAES.MC(state) print("MixColumns\t", list(state)) return list(state) data = [0]*16 data[-1] = 0xff print("=== Plain AES ===\n") s = aes_round_0(data) print("State after round 0\t", s) print("\n=== WB AES ===\n") s = aes_round_0_whiteboxed(data) print("State after round 0\t", s)
=== Plain AES === Original state [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 255] AddRoundKey [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 254] SubstituteBytes [124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 187] ShiftRows [124, 124, 124, 187, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124] MixColumns [187, 187, 46, 233, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124] State after round 0 [187, 187, 46, 233, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124] === WB AES === Original state [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 255] State after round 0 [187, 187, 46, 233, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124]
In the whiteboxed AES, the only thing observable is the original state and the state at the end of the round, the latter being produced using lookups into precomputed tables. The round key does not appear anywhere in the computation of the state (or at least, does not appear in clear).
Great, the key is hidden, but is that enough to protect it from being stolen? Obviously not, if you can do a bit of maths (and I can’t do maths either) it is pretty trivial to reverse the AES algorithm on a single round to recover the round key that was used. That is basically just the decryption process on a single round, as you can see below:
def reverse_round_0(state, original_data): state = phoenixAES.InvMC(state) state = phoenixAES.InvShiftRow(state) state = phoenixAES.InvSBox(state) key = [state[i]^original_data[i] for i in range(16)] return list(key) # final state computed previously final_state = [187, 187, 46, 233, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124] print("=== Rewind AES round 0 ===") k = reverse_round_0(final_state, original_data=data) print("Recovered key\t", k)
=== Rewind AES round 0 === Recovered key [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
Internal encodings to protect whiteboxes
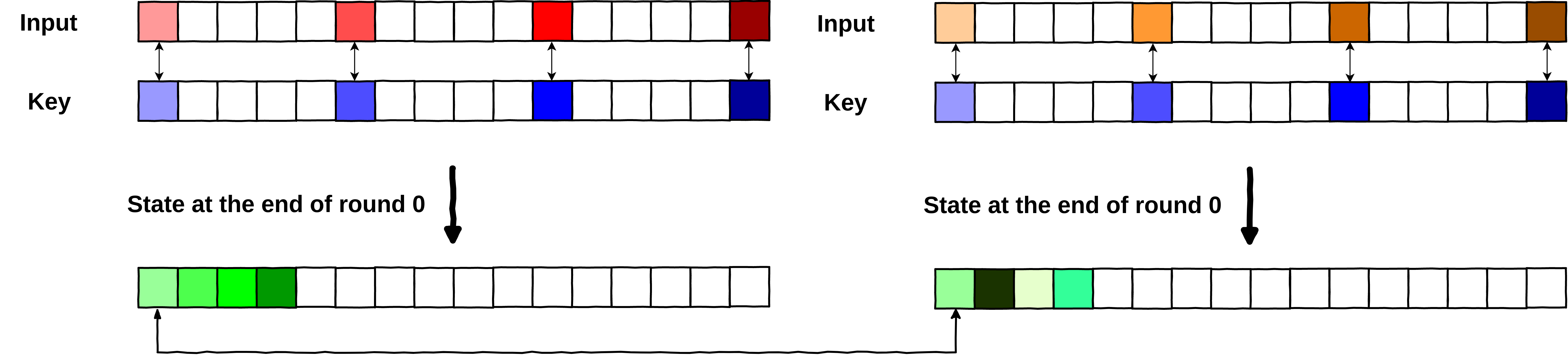
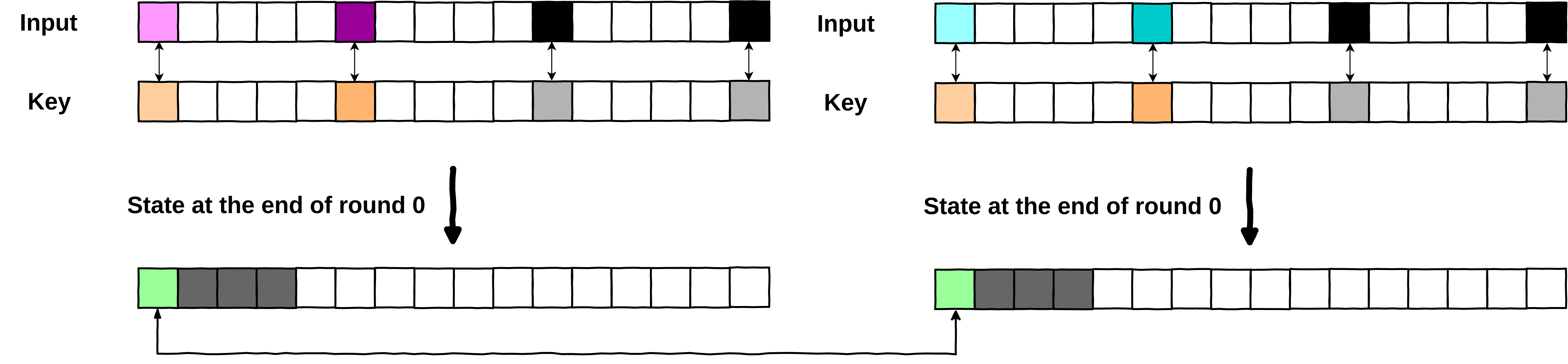
With the key being “hidden” in the precomputed tables, we already moved a step forward, but as we saw, an attacker who can encrypt a block of data, and who can observe the state of the AES at the end of the first round, could trivially recover the used key (because he knows both the input data and the final state). That is an issue that whiteboxes designers try to solve using what is called internal encodings.
I won’t go into the full design and purpose of those (because it’s maths, and crypto... :( ), but basically the point is to not let an attacker observe the state of AES in clear at any point during the algorithm. For this, typically, each byte is encoded into another using a bijective function (so each input byte has only one corresponding output byte, and the other way around).
If you were to observe the state at the end of a round, you would not be able to recover the key, without knowing this bijection. (And such bijection is precomputed into the tables... things start to get messy!)
Let’s have an example below. We will take the final_state previously computed, and suppose that the bijection (for x in [0,256]) used in the tables was:
\begin{equation*} f(x) = (x+1) \% 256 \end{equation*}
With that encoded state, can we recover the key?
# final state computed previously final_state = [187, 187, 46, 233, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124] encoded_state = [(x+1)%256 for x in final_state] data = [0]*16 data[-1] = 0xff print("=== Rewind AES round 0 ===") print("Encoded state\t", encoded_state) k = reverse_round_0(final_state, original_data=data) print("Recovered key (from plain state)\t", k) k = reverse_round_0(encoded_state, original_data=data) print("Recovered key (from encoded state)\t", k)
=== Rewind AES round 0 === Encoded state [188, 188, 47, 234, 125, 125, 125, 125, 125, 125, 125, 125, 125, 125, 125, 125] Recovered key (from plain state) [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1] Recovered key (from encoded state) [44, 19, 19, 19, 19, 63, 19, 19, 19, 19, 143, 19, 19, 19, 19, 193]
So, it seems that the encodings are quite effective! An almighty attacker with debugging capabilities could not recover the key just by reverting the round!
Note: In the previous example, we applied the encoding after the round of AES has been performed. In a whiteboxed-AES, this is precomputed in the tables, so you never see the clear state, at any time.
More about internal encodings
So, internal encodings are effective, but we are altering AES computations, so that is not really AES anymore? Well, the way internal encodings are used keeps a pure AES. In fact, the encoding applied during a step \(x\), is cancelled during step \(x+1\) before applying the new encoding. For instance, let’s take the following encodings for round 0 and 1:
\begin{equation*} f_0(x) = (x+1) \% 256 \end{equation*}
\begin{equation*} f_1(x) = (x+2) \% 256 \end{equation*}
The lookup tables of the round 1 would in fact be created by first using the inverse function of \(f_0\):
\begin{equation*} f^{-1}_0(x) = (x-1) \% 256 \end{equation*}
And would then apply \(f_1(x)\). All of this precomputed in the lookup tables, so completely invisible to the attacker.
There is still one issue though, what happens after the final round? We need to get the same output as a non-whiteboxed, so for sure there can’t be any encodings there (or the decrypted media would not play). So the attacker could just look at the output of the whiteboxed AES, and recover the last round key?
Not exactly. When we recovered the round key of round 0, one thing we needed was the previous state (being the first round, the state is just the plain input). Here, even with all powers, we could only observe an encoded state, which does not fit the requirement to rollback the round of AES.
Finally, a few things worth mentioning:
- In the examples we used a really simple (linear) encoding function, that might be trivially cracked by an attacker. Whiteboxes can use much more complex (non-linear) encodings, making bruteforcing of those quite laborious.
- In the examples, all the bytes were encoded using the same function. Usually, every byte is encoded using a different bijection. (That's not 100% accurate, as the more encodings you have, the bigger your lookup table is. There is a tendency to reuse some of them, or find some kind of tradeoff not to get a massive binary)
If you want to dig further, there are lots of papers dealing with internal encodings (beginning with the original paper of Chow [5] ). You can also look for external encodings ([2] ) which are another way to protect whiteboxes, but are not the subject of this post. Defeating those implies using different techniques, but the use of external encoding can be quite bothersome to use.
Defeating whiteboxes: a collision-based attack
About whiteboxes attacks
Attacks against whiteboxes exist since the first whitebox design. There are many ways to attack those, from static reversing or encoding recovery, to statistical approaches [6] or even fault-based ones [7]. There are lots of great posts, papers and presentations out there, but it may not be that easy to understand when you are freshly dropped into the whitebox world.
There is another attack that I found while digging around the subject. I find it quite interesting and easy to understand so that is the one we will use to attack a demo whitebox and recover the key.
Note: Collisions-based attacks are not new, I believe they have been known for a while as similar attacks were explained both in Chow's original paper and more recently in a 2019 paper by CryptoExperts [8]. I can't say for sure they are the same attacks though as I do not speak the Mordor language.
Building an attack from the ground up
Note: The following part summarizes the thought process I had while building the attack. If you are already well familiar with AES, you might want to skip a few sections.
Before diving into the attack, we need to figure out a few AES properties that come from the structure of the operations of the algorithm.
AES Property: bytes relationship
As previously listed, there are 4 operations that build a round of AES. Each of them is really specific, and they give interesting cryptographic properties when combined. Those operations combined multiple times (rounds) make AES a strong cryptographic algorithm. However, when combined only a few number of times, they can be exploited to grab some information about the key being used by the algorithm.
That is what we will try to do, by analyzing a single round of AES (round 0).
Let’s do a round of AES with different plaintexts, and observe what the AES state looks like at the end. More specifically, we will fix the whole plaintext to a stable value, except one byte that we will iterate over [0,255].
import phoenixAES def aes_round_0(state, key): state=phoenixAES.AddKey(state, key) state=phoenixAES.SBox(state) state=phoenixAES.ShiftRow(state) state=phoenixAES.MC(state) return list(state) data = [0]*16 key = [0]*16 states = [] for i in range(0,256): data[0] = i states.append(aes_round_0(data, key)) states[0:4]
[[99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99], [93, 124, 124, 66, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99], [75, 119, 119, 95, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99], [83, 123, 123, 75, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99]]
Interestingly, when we tweak a single input byte, only 4 output bytes are affected. If we plot those values, it becomes quite visible (The graph below is animated, feel free to play around with it :) ).
import plotly.express as px import plotly.graph_objects as go fig = go.Figure() fig.update_layout( title="Values of each byte of the state with different plaintext", xaxis_title="state byte index", yaxis_title="byte value", ) for i, state in enumerate(states): # Shift data a bit, so it is visible on plot x_values = [(0.001*i)+x for x in range(16)] y_values = state fig.add_trace(go.Scatter(x=x_values, y=y_values, mode='markers', name=F"Plaintext_b0={i}"), ) fig.show()
This comes from the MixColumn operation, that merges together 4 bytes to generate the output byte.
If we have a look at the example at the very beginning of the article, we see that before the MixColumn operation, one byte of input is in relation with only one byte of the key (that happens during AddRoundKey).
=== Plain AES === Original state [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 255] AddRoundKey [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 254] SubstituteBytes [124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 187] ShiftRows [124, 124, 124, 187, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124] MixColumns [187, 187, 46, 233, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124] FinalState [187, 187, 46, 233, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124]
The MixColumns operation is mixing bytes together. The input bytes that are mixed together, and the affected output bytes are summarized below:
- Modifying input bytes [0,5,10,15] will affect output bytes [0,1,2,3] (see example below)
- Modifying input bytes [1,6,11,12] will affect output bytes [4,5,6,7]
- Modifying input bytes [2,7,8,13] will affect output bytes [8,9,10,11]
- Modifying input bytes [3,4,9,14] will affect output bytes [12,13,14,15]
When this mix is done, you've reached the end of a round, and can observe an intermediate state of AES.
- Observation: One byte of the input has an impact to 4 bytes of the output.
A round of AES can basically be split into 4 blocks of independent operations, which allows us to observe and play with 1/4 of the state without impacting the rest of the state.
For the rest of the post, examples will be based on \(input\_bytes = [0,5,10,15]\) and \(output\_bytes = [0,1,2,3]\). The rest of the input and output bytes should not be considered, as they are independent.
AES property: state collisions
With that first observation, we can start playing around with 1/4 of the input bytes. Let’s consider a plain AES (no whitebox), and run a single round of AES on two different plaintexts, with the same key.
RELATIONSHIP = [ {"affected_bytes":[0,1,2,3], "input_bytes":[0, 5, 10, 15]}, {"affected_bytes":[4,5,6,7], "input_bytes":[1, 6, 11, 12]}, {"affected_bytes":[8,9,10,11], "input_bytes":[2, 7, 8, 13]}, {"affected_bytes":[12,13,14,15], "input_bytes":[3, 4, 9, 14]}, ] r = RELATIONSHIP[0] data0 = [0]*16 data1 = [0]*16 for i, byte_index in enumerate(r["input_bytes"]): data0[byte_index] = i data1[byte_index] = i+4 key = [0]*16 s0 = aes_round_0(data0, key) s1 = aes_round_0(data1, key) print(F"Encrypting \t{data0} \n\t= \t{s0}") print(F"Encrypting \t{data1} \n\t= \t{s1}")
Encrypting [0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 2, 0, 0, 0, 0, 3]
= [78, 121, 124, 88, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99]
Encrypting [4, 0, 0, 0, 0, 5, 0, 0, 0, 0, 6, 0, 0, 0, 0, 7]
= [232, 80, 19, 152, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99]
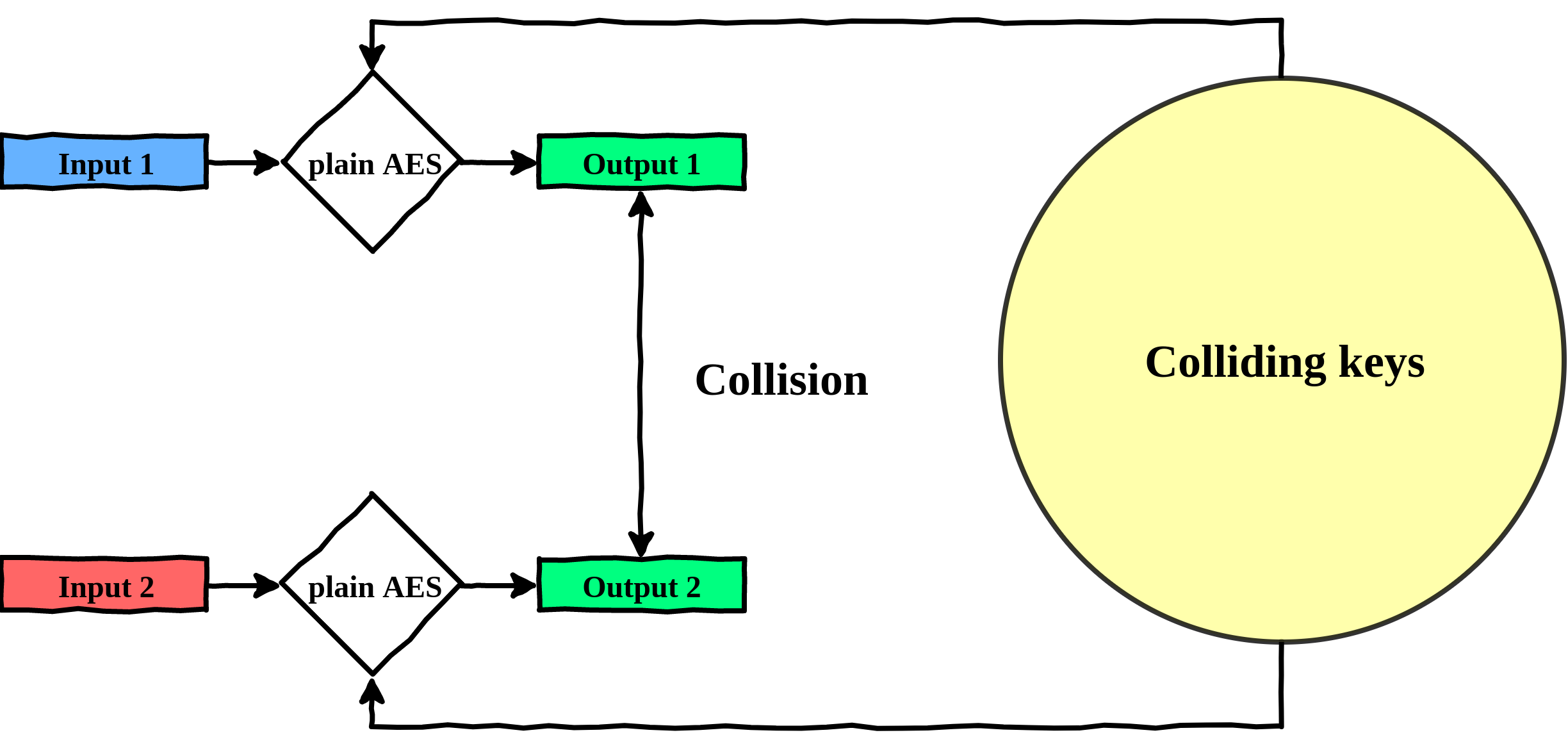
So what to observe here? We used two different plaintexts, with the same key, and got two different states. Nothing surprising, two different plaintexts will always give you two different states.
Two different plaintexts yield
two different AES states at the end of round 0.
Let’s have a look at another pair of plaintexts, that we chose carefully for the example.
data0 = [0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 2, 0, 0, 0, 0, 3] data1 = [47, 0, 0, 0, 0, 183, 0, 0, 0, 0, 48, 0, 0, 0, 0, 58] key = [0]*16 s0 = aes_round_0(data0, key) s1 = aes_round_0(data1, key) print(F"Encrypting \t{data0} \n\t= \t{s0}") print(F"Encrypting \t{data1} \n\t= \t{s1}")
Encrypting [0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 2, 0, 0, 0, 0, 3]
= [78, 121, 124, 88, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99]
Encrypting [47, 0, 0, 0, 0, 183, 0, 0, 0, 0, 48, 0, 0, 0, 0, 58]
= [78, 208, 47, 137, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99]
Here again, two different plaintexts yield different outputs, however, there is something worth noticing. One of the output bytes is the same in both states. Both states have \(b_0 = 78\). This is what we call a collision in the rest of the post. (Remember, we are only looking at the impacted bytes, so \(b_0, b_1, b_2, b_3\))
Two different plaintexts can
yield identical bytes at the end of round 0.
Those collisions are interesting in many ways. The first thing worth noticing, is that this collision exists for this very specific key, \(key = [0]*16\). We would not get a collision with the same set of inputs and another key (see the example below with \(key = [1]*16\)).
Note: That is not really true, many different keys would yield a collision on this byte. However, for the sake of the explanation, let’s consider that the collision happens only for this specific key. Later we will talk about a key distinguisher to isolate the real key, from all the potential ones.
data0 = [0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 2, 0, 0, 0, 0, 3] data1 = [47, 0, 0, 0, 0, 183, 0, 0, 0, 0, 48, 0, 0, 0, 0, 58] key = [1]*16 s0 = aes_round_0(data0, key) s1 = aes_round_0(data1, key) print(F"Encrypting \t{data0} \n\t= \t{s0}") print(F"Encrypting \t{data1} \n\t= \t{s1}")
Encrypting [0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 2, 0, 0, 0, 0, 3]
= [81, 64, 112, 114, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124]
Encrypting [47, 0, 0, 0, 0, 183, 0, 0, 0, 0, 48, 0, 0, 0, 0, 58]
= [149, 29, 215, 5, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124, 124]
As previously stated, changing the key results in new states, and no collision can be observed this time. This is pretty interesting.
If we were running an AES with an unknown key, and could observe such collision, by running AES_round_0 on those two plaintexts, and iterating over all the potential keys, we could identify the good one, just by looking for this collision (Remember, there is still that key distinguisher to consider).
But the thing is, we don’t face a standard AES. A whiteboxed-AES uses its internal encodings to hide the real value of the bytes. But is that enough? Not in this case.
Indeed, internal encodings use bijections. It means that a specific byte, is always encoded in the same way, there is no randomness involved. So it means that (second property we need):
- Observation: If we are able to observe a collision on encoded states, that collision also exists on plain states.
Or, as stated by Chow [5]: “two texts which have the same encoded value in that cell, have the same unencoded value in that cell.”
You can find below an example with the previous colliding states and the encoding function \(f(x) = (x+1)%256\). We can observe that \(b_0\) is still identical between the two states.
s0 = [78, 121, 124, 88, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99] s1 = [78, 208, 47, 137, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99] encoded_s0 = [(x+1)%256 for x in s0] encoded_s1 = [(x+1)%256 for x in s1] print("encoded state 0 : ", encoded_s0) print("encoded state 1 : ", encoded_s1)
encoded state 0 : [79, 122, 125, 89, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100] encoded state 1 : [79, 209, 48, 138, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100]
So what does this mean for us? It means that we could:
- Find 2 different plaintexts that have a collision between bytes of the output after a round of whiteboxed AES.
- Select those 2 same plaintexts, and iterate over all the potential keys on a non-whiteboxed AES, until we get that collision.
- Once we get a collision, we found the key! (again, there would be many candidates that we will filter later).
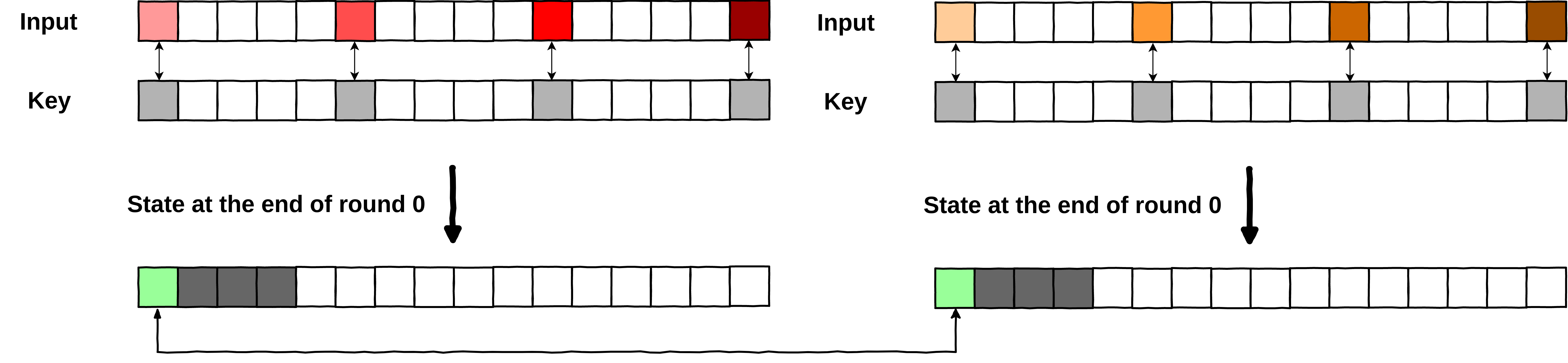Step 1. Find a collision
between 2 plaintexts on whiteboxed-AES
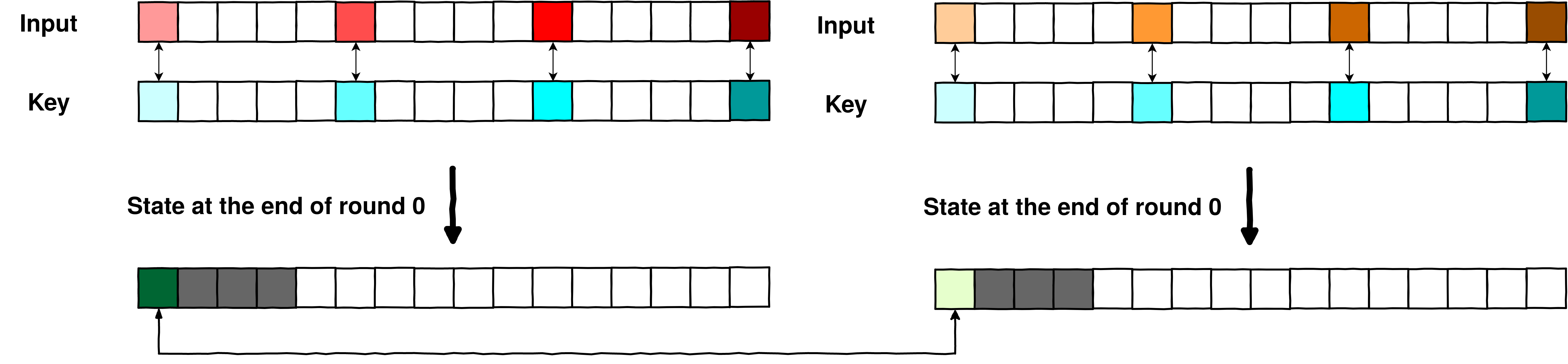Step 2. Look for a colliding key on a plain AES
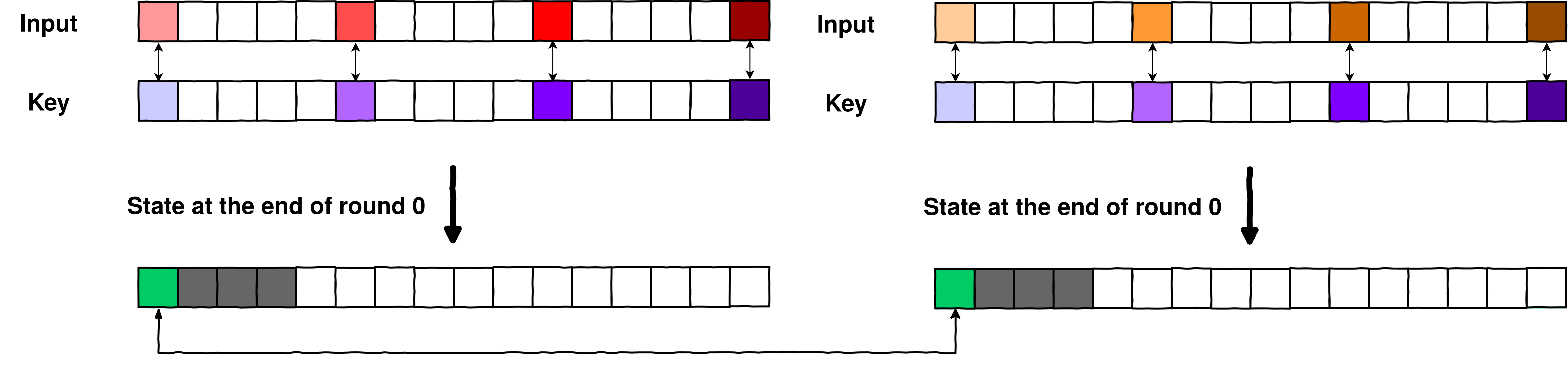Step 3. Colliding key found
That is great! However, this would be really slow. We are looking at 1/4 of the AES, but even broken down in 4 parts, those "sub-keys" are still 32-bits long. That would require quite some computations to test all the potential keys... (And we would have to do that 4 times, to break the 4 independent blocks of the key). We will deal with that in the following part, Improving collisions-based attacks. For the sake of the explanation, we will still perform the attack below, but with a reduced number of keys to test, to demonstrate the feasibility.
# Supposed whitebox, with a specific key, and a simple internal encoding. def whitebox(state): # Only useful bytes are [0,5,10,15] key = [222, 12, 12, 12, 12, 173, 12, 12, 12, 12, 190, 12, 12, 12, 12, 239] state=phoenixAES.AddKey(state, key) state=phoenixAES.SBox(state) state=phoenixAES.ShiftRow(state) state=phoenixAES.MC(state) state = [(x+1)%256 for x in list(state)] return list(state) data0 = [0]*16 data1 = [98, 0, 0, 0, 0, 78, 0, 0, 0, 0, 165, 0, 0, 0, 0, 52] # computing whiteboxed states for two plaintexts that give a collision. wb_s0 = whitebox(data0) wb_s1 = whitebox(data1) print(F"[WHITEBOX] We have a collision between plaintexts (on byte_0):") print(F"Plain0 = \t{data0}\nstate = \t{wb_s0}\n") print(F"Plain1 = \t{data1}\nstate = \t{wb_s1}\n") print("Supposed \"Exhaustive\" lookup of potential keys over 2^32 possibilities.\n") reduced_potential_keys = [ [21, 0, 0, 0, 0, 207, 0, 0, 0, 0, 114, 0, 0, 0, 0, 40], [164, 0, 0, 0, 0, 126, 0, 0, 0, 0, 118, 0, 0, 0, 0, 183], [62, 0, 0, 0, 0, 138, 0, 0, 0, 0, 68, 0, 0, 0, 0, 62], [0xde, 0, 0, 0, 0, 0xad, 0, 0, 0, 0, 0xbe, 0, 0, 0, 0, 0xef], ] # Iterate over all the key space, to find one key that generate a collision # on a plain AES. for key in reduced_potential_keys: s0 = aes_round_0(data0, key) s1 = aes_round_0(data1, key) # Check if we have a collision on byte 0 (we could also look for collisions on bytes 1,2,3) if s0[0] == s1[0]: print(F"[PLAIN] Found a key that gives a collision on byte_0 for :") print(F"Plain0 = \t{data0}\nstate = \t{s0}\n") print(F"Plain1 = \t{data1}\nstate = \t{s1}\n") print(F"4-bytes-key is : {key}")
[WHITEBOX] We have a collision between plaintexts (on byte_0): Plain0 = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] state = [240, 27, 182, 186, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255] Plain1 = [98, 0, 0, 0, 0, 78, 0, 0, 0, 0, 165, 0, 0, 0, 0, 52] state = [240, 21, 226, 121, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255] Supposed "Exhaustive" lookup of potential keys over 2^32 possibilities. [PLAIN] Found a key that gives a collision on byte_0 for : Plain0 = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] state = [239, 26, 181, 185, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99] Plain1 = [98, 0, 0, 0, 0, 78, 0, 0, 0, 0, 165, 0, 0, 0, 0, 52] state = [239, 20, 225, 120, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99] 4-bytes-key is : [222, 0, 0, 0, 0, 173, 0, 0, 0, 0, 190, 0, 0, 0, 0, 239]
As we can see, when using the right key (the 4 bytes of the key involved actually), we observe a collision, both on the whiteboxed and plain AES, despite the presence of internal encodings. It works, but it is obviously not practical because of the number of keys we would need to test. So let’s try to make this attack a bit better, by reducing the key-space.
Improving collisions-based attacks
The main issue we have from the collision-based attack previously described, is that it would require to test all the potential keys over a range of \(2^{32}\) possibilities (Actually, even more, because to distinguish the key, we would need to do that multiple times).
Would it be possible to reduce it? For instance, to break the key bit by bit? Or byte by byte?
The idea is to reduce the number of keys we need to test. To do so, we need to find a way to get a few bytes of the key, out of the equation. To get to this result, we can experiment around by modifying only a single byte of input, and keep the rest of them static.
If we do so, we quickly realize that if we modify a single byte, we will never find a collision. (Iterating a single byte of input over \([0,255]\), would result in the 4 impacted bytes to take all values in \([0,255]\). If that was not the case, AES would be biased and not cryptographically secure).
So, we need to modify at least 2 bytes of input, to get a collision. Let’s have a look at the following collision where we modified only 2 input bytes (\(Ib_0\) and \(Ib_5\)), and kept the 2 remaining ones (\(Ib_{10}\) and \(Ib_{15}\)) at a fixed value (here the value is \(0\)).
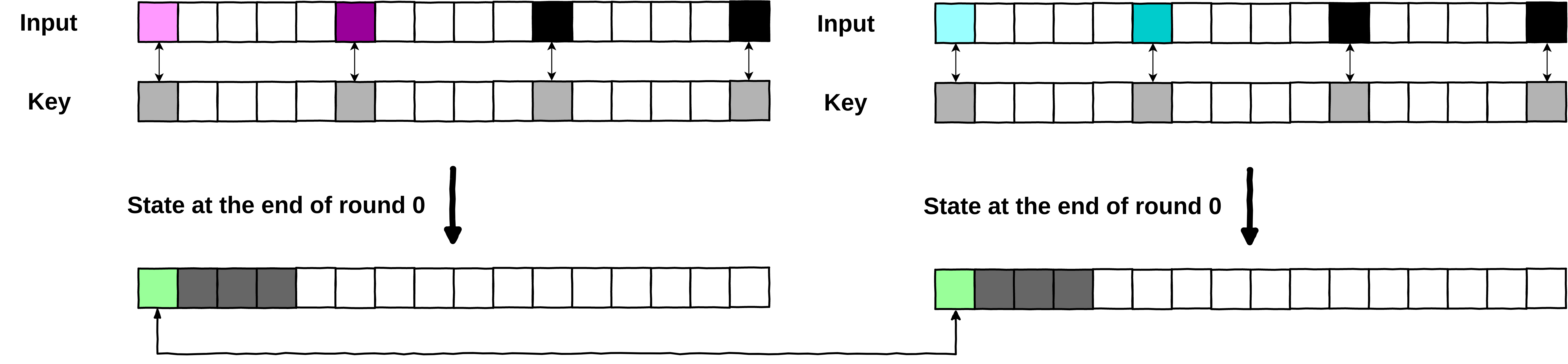Whitebox collision with only 2 input bytes
modified
We can easily identify a collision on the output byte \(Ob_0 = 240\).
data1 = [0]*16 data0 = [207, 0, 0, 0, 0, 198, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] s0 = whitebox(data0) s1 = whitebox(data1) print(F"Plain0 = \t{data0}\nstate = \t{s0}\n") print(F"Plain1 = \t{data1}\nstate = \t{s1}\n")
Plain0 = [207, 0, 0, 0, 0, 198, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] state = [240, 75, 193, 234, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255] Plain1 = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] state = [240, 27, 182, 186, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255]
Now what happens if we decide to modify a third byte of the input?
data0[10] = 10 s0 = whitebox(data0) s1 = whitebox(data1) print(F"Plain0 = \t{data0}\nstate = \t{s0}\n") print(F"Plain1 = \t{data1}\nstate = \t{s1}\n")
Plain0 = [207, 0, 0, 0, 0, 198, 0, 0, 0, 0, 10, 0, 0, 0, 0, 0] state = [205, 48, 135, 203, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255] Plain1 = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] state = [240, 27, 182, 186, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255]
Without much surprise, the collision is no more. However, one interesting thing is that if we modify that third byte on both inputs, and we set it to the same value, the collision is back on \(Ob_0\), but this time with a different value \(Ob_0 = 205\). No matter what value we put in the two remaining bytes, if they are the same on both plaintexts, the collision will still happen.
data0[10] = 10 data1[10] = 10 s0 = whitebox(data0) s1 = whitebox(data1) print(F"Plain0 = \t{data0}\nstate = \t{s0}\n") print(F"Plain1 = \t{data1}\nstate = \t{s1}\n")
Plain0 = [207, 0, 0, 0, 0, 198, 0, 0, 0, 0, 10, 0, 0, 0, 0, 0] state = [205, 48, 135, 203, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255] Plain1 = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10, 0, 0, 0, 0, 0] state = [205, 128, 244, 155, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255]
So what are we really observing, and what does it mean for the attack?
- The \(Ob_0\) value is dependent on \(Ib_0\), \(Ib_5\), \(Ib_{10}\), and \(Ib_{15}\).
However:
- The existence of a collision is dependent only on the varying bytes (in our case \(Ib_0\) and \(Ib_5\)).
I will not bother you (too much) with the maths, just think that \(b_0\) is computed as something similar to:
\begin{equation*} b_0 = f(x_0, k_0) \oplus g(x_5, k_5) \oplus h(x_{10}, k_{10}) \oplus i(x_{15}, k_{15}) \end{equation*}
- \(\oplus\) being XOR
- \(x_i\) the input
- \(k_i\) the key
- \(i\) the byte index
- \(f, g, h, i\) are functions that come from all the AES operations, but we don’t really care about what they are doing, we just need to know they are different
In our case, \(x_{10}\), \(x_{15}\), \(k_{10}\), \(k_{15}\) are constant, so the last two terms are also constant and we end up with something like:
\begin{equation*} b_0 = f(x_0, k_0) \oplus g(x_5, k_5) \oplus C \end{equation*}
That constant \(C\) being the same on both plaintexts, we end up with a collision dependent only on \(x_0\), \(x_5\), \(k_0\) and \(k_5\). And that is the last observation we need for the attack.
- Observation: We can compute collisions that depend only on a reduced part of the key, if we keep a part of the input constant.
With this observation, we know that if a collision is happening, \(k_{10}\) and \(k_{15}\) are not relevant in the existence of the collision, since we fixed \(x_{10}\) and \(x_{15}\).
So it means that:
- We find 2 plaintexts, that differ only on two bytes that generate a collision through the whitebox.
- Then when we will look for the proper key, instead of trying all the potential keys over a \(2^{32}\) space, we will instead try to break 2 bytes of the key, reducing the potential keys to test to \(2^{16}\) possibilities (obviously, we need to run this twice, to break the 2 remaining bytes of key, so it is in the end \(2^{17}\) keys at most).
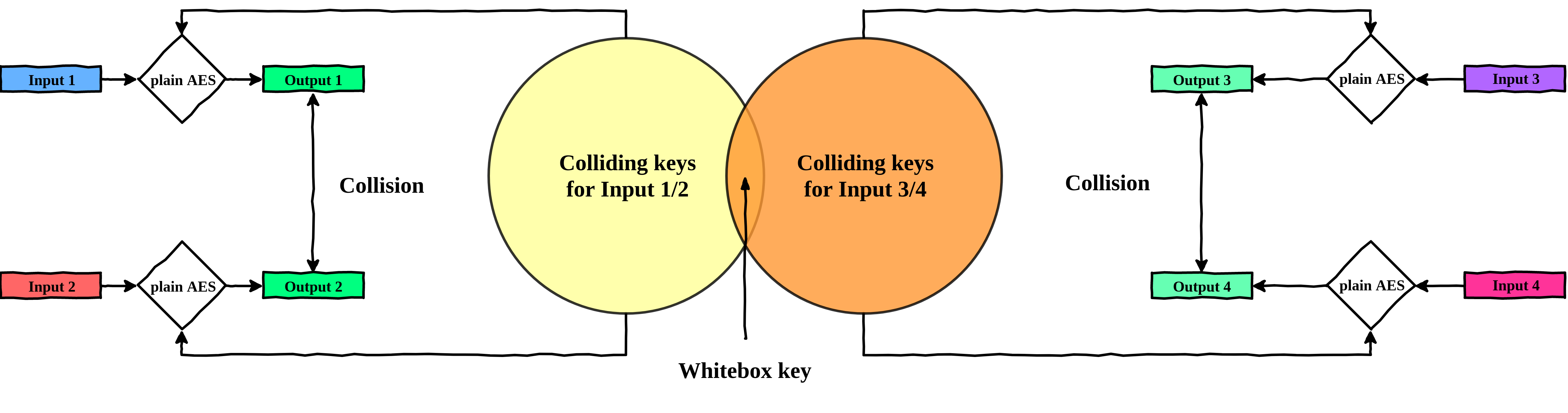
Looking for a key generating collisions for the
pair of plaintexts
Now we can get to a real key recovery (and can finally talk about the key distinguisher):
# Colliding pair of plaintexts for the whitebox data1 = [0]*16 data0 = [207, 0, 0, 0, 0, 198, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] s0 = whitebox(data0) s1 = whitebox(data1) print(F"Plain0 = \t{data0}\nstate = \t{s0}\n") print(F"Plain1 = \t{data1}\nstate = \t{s1}\n") # key to recover wb_key = [222, 12, 12, 12, 12, 173, 12, 12, 12, 12, 190, 12, 12, 12, 12, 239] # Iterate over all the key space, to find one key that generates a collision # on a plain AES. colliding_keys = [] for i in range(256): for j in range(256): key = [0]*16 key[0] = i key[5] = j s0 = aes_round_0(data0, key) s1 = aes_round_0(data1, key) # Check if we have a collision on byte 0 (we could also look for collisions on bytes 1,2,3) if s0[0] == s1[0]: colliding_keys.append(key) if wb_key[0] == i and wb_key[5] == j: print("Key found !") print("Key : \t\t", key) print("Wb_key : \t", wb_key) break print("Number of potential keys found : ", len(colliding_keys))
Plain0 = [207, 0, 0, 0, 0, 198, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] state = [240, 75, 193, 234, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255] Plain1 = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] state = [240, 27, 182, 186, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255] Key found ! Key : [222, 0, 0, 0, 0, 173, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] Wb_key : [222, 12, 12, 12, 12, 173, 12, 12, 12, 12, 190, 12, 12, 12, 12, 239] Number of potential keys found : 280
Key generating a collision on the pair of plaintexts
found
Isolating the real key
As we can see in the previous snippet, we manage to recover \(k_0\) and \(k_5\) based on the two colliding plaintexts we identified. That is pretty neat, however, as you noticed, we found 280 keys that were generating a collision... Here it was easy to identify the good one, since we know the key held in the whitebox (but usually that is not the case, otherwise we would not be here :D).
So how can we distinguish the real key from the rest? Well this is actually quite simple. We just need a few more pairs of colliding inputs.
Indeed, for a given pair of plaintexts, there are many different keys that could yield a collision. However, for another given pair of plaintexts, there would also be many different keys, but they would not all be the same. If we do an intersection of the potential keys, we can find the only good key!
Note: You might need more than just two pairs of plaintexts to distinguish the real key.
Isolate the good key by intersecting the potential
keys for two pair of plaintexts
Demonstration of the attack
Below is a full example of how to perform the attack. To make it a bit cleaner to read, we pre-selected 3 pairs of colliding inputs.
from pprint import pprint # Find all keys generating a collision for a given pair of input def find_colliding_keys(p0, p1): # Iterate over all the key space, to find one key that generate a collision # on a plain AES. colliding_keys = [] ctr = 0 for i in range(256): for j in range(256): key = [0]*16 key[0] = i key[5] = j s0 = aes_round_0(p0, key) s1 = aes_round_0(p1, key) # Check if we have a collision on byte 0 (we could also look for collisions on bytes 1,2,3) if s0[0] == s1[0]: colliding_keys.append(key) return colliding_keys # Pair of colliding plaintexts input1 = [16, 0, 0, 0, 0, 55, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] input2 = [12, 0, 0, 0, 0, 17, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] # Pair of colliding plaintexts input3 = [91, 0, 0, 0, 0, 229, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] input4 = [99, 0, 0, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] # Pair of colliding plaintexts input5 = [170, 0, 0, 0, 0, 85, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] input6 = [217, 0, 0, 0, 0, 210, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] # Verify that collisions are indeed existing after a round of whitebox s1 = whitebox(input1) s2 = whitebox(input2) print(F"Plain1 = \t{input1}\nstate = \t{s1}\n") print(F"Plain2 = \t{input2}\nstate = \t{s2}\n") s3 = whitebox(input3) s4 = whitebox(input4) print(F"Plain3 = \t{input3}\nstate = \t{s3}\n") print(F"Plain4 = \t{input4}\nstate = \t{s4}\n") # Look for potential keys c0 = find_colliding_keys(input1, input2) print(F"==>\tc0 has {len(c0)} potential keys") c1 = find_colliding_keys(input3, input4) print(F"==>\tc1 has {len(c1)} potential keys") # Keep only common potential keys by doing an intersection set_c0 = set([bytes(i) for i in c0]) set_c1 = set([bytes(i) for i in c1]) pk = set_c0.intersection(set_c1) print("Potential keys with 2 pairs of plaintexts : \n") pprint(pk) print("-"*80) # Refine potential keys with a third pair of plaintexts s5 = whitebox(input5) s6 = whitebox(input6) print(F"Plain5 = \t{input5}\nstate = \t{s5}\n") print(F"Plain6 = \t{input6}\nstate = \t{s6}\n") c2 = find_colliding_keys(input5, input6) print(F"==>\tc2 has {len(c2)} potential keys") # Set of potential keys is now unique, we found the good key ! set_c2 = set([bytes(i) for i in c2]) pk = pk.intersection(set_c2) print("Potential keys with 3 pairs of plaintexts : ") print(pk) print("-"*80) # Key to recover wb_key = [222, 12, 12, 12, 12, 173, 12, 12, 12, 12, 190, 12, 12, 12, 12, 239] print("\nVerifying that we found the good key-bytes") recovered_key = list(pk.pop()) print(F"recovered_key\t= {recovered_key}\nwhitebox_key\t= {wb_key}") print("recovered_key[0] == wk_key[0] : ", recovered_key[0] == wb_key[0]) print("recovered_key[5] == wk_key[5] : ", recovered_key[5] == wb_key[5])
Plain1 = [16, 0, 0, 0, 0, 55, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
state = [176, 215, 15, 54, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255]
Plain2 = [12, 0, 0, 0, 0, 17, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
state = [176, 74, 238, 171, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255]
Plain3 = [91, 0, 0, 0, 0, 229, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
state = [179, 6, 249, 252, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255]
Plain4 = [99, 0, 0, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
state = [179, 160, 164, 98, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255]
==> c0 has 264 potential keys
==> c1 has 284 potential keys
Potential keys with 2 pairs of plaintexts :
{b'.\x00\x00\x00\x00\xf0\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00',
b'\xb5\x00\x00\x00\x00c\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00',
b'\xde\x00\x00\x00\x00\xad\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00'}
--------------------------------------------------------------------------------
Plain5 = [170, 0, 0, 0, 0, 85, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
state = [142, 39, 239, 232, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255]
Plain6 = [217, 0, 0, 0, 0, 210, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
state = [142, 77, 43, 142, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255]
==> c2 has 268 potential keys
Potential keys with 3 pairs of plaintexts :
{b'\xde\x00\x00\x00\x00\xad\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00'}
--------------------------------------------------------------------------------
Verifying that we found the good key-bytes
recovered_key = [222, 0, 0, 0, 0, 173, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
whitebox_key = [222, 12, 12, 12, 12, 173, 12, 12, 12, 12, 190, 12, 12, 12, 12, 239]
recovered_key[0] == wk_key[0] : True
recovered_key[5] == wk_key[5] : True
Finalizing the attack
As you can see above, with 3 pairs of colliding plaintexts, we managed to recover 2 bytes of the key: \(Ob_0\) and \(Ob_5\). If we wanted to recover \(Ob_{10}\) and \(Ob_{15}\) we would need to set \(Ib_0\) and \(Ib_5\) to a fixed value, find collisions by modifying \(Ib_{10}\) and \(Ib_{15}\), and finally look for a colliding key, by iterating over all the possible values of \(k_{10}\) and \(k_{15}\).
Doing this, we would break 4 bytes of the key, and we can do this operation for the 3 last independent parts of AES, to recover the full first round key (which is equal to the original AES-128 key)!
To demonstrate the feasibility, we will be looking at an example, and break it using the collision-based attack we just described.
Defeating whiteboxes: a QBDI showcase
Our target: GreHack2019 whitebox
As a demonstration, I decided to look into the most recent whitebox I could find. Thanksfully, SideChannelMarvels has a repository full of already broken whiteboxes [9]. There is one from 2019, from GreHack 2019 CTF, already broken by a few researchers [10] [11], so let’s get started with this one.
The challenge is composed of 3 files:
- enc.c: contains the definition of the encrypt() function
- instr.c: content of the encrypt() function
- tables.h: 2 Mb header of hardcoded values (whitebox tables)
This is what enc.c looks like:
void encrypt (uint8_t *buffer) { uint8_t s[42]; memcpy(s, buffer, 16); #include "instr.c" memcpy(buffer, s, 16); }
The encrypt function takes a 16-byte input (plaintext to encrypt), and puts it in an unknown structure. Following this, some magic is performed in instr.c, and finally, a 16-byte output is copied from the unknown structure back to the input buffer (encrypted plaintext).
We can compile this as a shared library, so we can call the encrypt() function easily.
gcc enc.c -shared -fpic -o wb.so
Analyzing the target with QBDI
So far, we have absolutely no information about what is happening in that encrypt() function. If you have a look at its source code, it is full of data lookups from the tables, so it is probably a whiteboxed algorithm. One common way to understand the behaviour of a program (especially for cryptographic ones), is to have a look at memory accesses, and their patterns. You can learn a lot about your target, just by analyzing how often, and in which order data is being accessed.
To do this, we will use QBDI [12], that is the perfect solution for this kind of traces.
Note: For this example, the sources of the whitebox were available, but this is not a requirement for QBDI.
Let’s get started, and run the encrypt() function with QBDI. Below is a full snippet to do so. What it does is the following:
- Load the whitebox as a library with ctypes
- Initialize a QBDI VM
- Allocate an input buffer (16 bytes), and write data to it
- Call the encrypt function with the freshly filled buffer as parameter
- Dump data from the same buffer (the encrypt function writes the encrypted block to it)
import pyqbdi import ctypes # Load the whitebox library using ctypes, and get a ptr to encrypt def load_wb(): wb = ctypes.cdll.LoadLibrary("./wb.so") encrypt_ptr = ctypes.cast(wb.encrypt, ctypes.c_void_p).value return encrypt_ptr def instanciate_vm(encrypt_ptr): # create a QBDI VM vm = pyqbdi.VM() vm.addInstrumentedModuleFromAddr(encrypt_ptr) # Allocate a stack for the QBDI vm state = vm.getGPRState() stack = pyqbdi.allocateVirtualStack(state, 0x1000000) return vm def encrypt(vm, encrypt_ptr, buffer_ptr, data): # backup registers gpr = vm.getGPRState() rsp = gpr.rsp ; rbp = gpr.rbp # write data to input buffer pyqbdi.writeMemory(buffer_ptr, bytes(data)) # encrypt and dump encrypted content success = vm.call(encrypt_ptr, [buffer_ptr]) state = pyqbdi.readMemory(buffer_ptr, 16) # restore registers gpr = vm.getGPRState() gpr.rsp = rsp ; gpr.rbp = rbp return state
def main(): encrypt_ptr = load_wb() vm = instanciate_vm(encrypt_ptr) buffer_ptr = pyqbdi.allocateMemory(16) state = encrypt(vm, encrypt_ptr, buffer_ptr, [0]*16) print(F"wb({[0]*16}) = \n\t", list(state)) main()
wb([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]) =
[200, 48, 81, 207, 15, 188, 94, 26, 143, 211, 192, 201, 176, 229, 73, 159]
Recording and visualizing memory accesses
With the previous snippet, we can easily encrypt an input, and observe its output. To learn a bit more about the algorithm, we will record and visualize every memory accesses it does. To do so, we will use the memory record feature from QBDI. Thanks to the snippet below, we can easily trace the memory accesses on a graph, and visualize them.
# Callback, called on every memory access def mem_cbk(vm, gpr, fpr, cb_data): accesses = cb_data["accesses"] stack = cb_data["stack"] buffer_ptr = cb_data["buffer_ptr"] # Keep a counter on the number of memory access ctr = cb_data["ctr"] memaccess = vm.getInstMemoryAccess() for acc in memaccess: rw_type = ["write", "read"][not (acc.type & pyqbdi.MEMORY_WRITE)] # If the accessed address is from the stack if acc.accessAddress in range(stack-0x1000000, stack): rw_type = "stack_" + rw_type # If the accessed address is from the provided buffer elif acc.accessAddress in range(buffer_ptr, buffer_ptr+16): rw_type = "buffer_" + rw_type # Store information about the memory access accesses.append({"id":ctr, "access": acc.accessAddress, "type":rw_type, "size":acc.size}) cb_data["ctr"] += 1 return pyqbdi.CONTINUE
def main(): encrypt_ptr = load_wb() vm = instanciate_vm(encrypt_ptr) buffer_ptr = pyqbdi.allocateMemory(16) # Add memory callback state = vm.getGPRState() cb_data = {"accesses":[], "ctr":0, "stack":state.rsp, "buffer_ptr":buffer_ptr} vm.addMemAccessCB(pyqbdi.MEMORY_READ_WRITE, mem_cbk, cb_data) state = encrypt(vm, encrypt_ptr, buffer_ptr, [0]*16) return cb_data memory_accesses = main()
import plotly.express as px fig = px.scatter(memory_accesses["accesses"], x="id", y="access", color="type", size="size") fig.show()
On the above graph, we can learn a lot, just by looking at how the accesses are performed (The graph is dynamic, you can play with it!).
- The X-axis is the id of the access. 0 being the very first memory access of the execution
- The Y-axis is the address accessed
First of all, if we filter the graph to keep only the read, we can see an almost linearly accessed flow of data. It’s not of much use, but those represent the accesses to the whitebox tables.
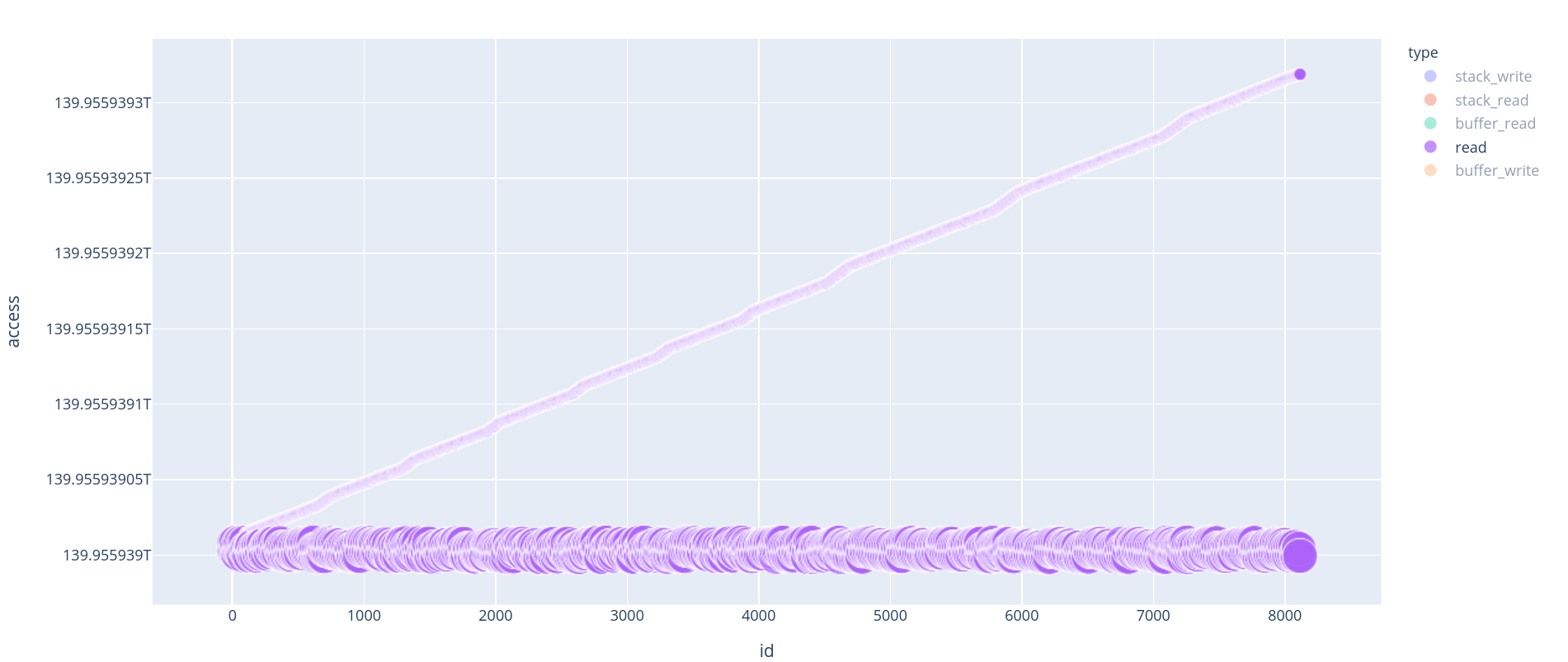Read accesses are the accesses to the whitebox
precomputed tables.
If we decide to look at stack_write or stack_read, things get really interesting. Indeed, we can see a repeating pattern. That pattern is repeated 10 times (the last 3 are a bit different, they look “mirrored”).
Those patterns are characteristic of an [en|de]cryption algorithm. In fact, those 10 blocks are rounds of AES. If we have 10 rounds, it means it is AES-128.
Note: The last 3 rounds are duplicated. This is a common way to protect against Fault injection attacks.
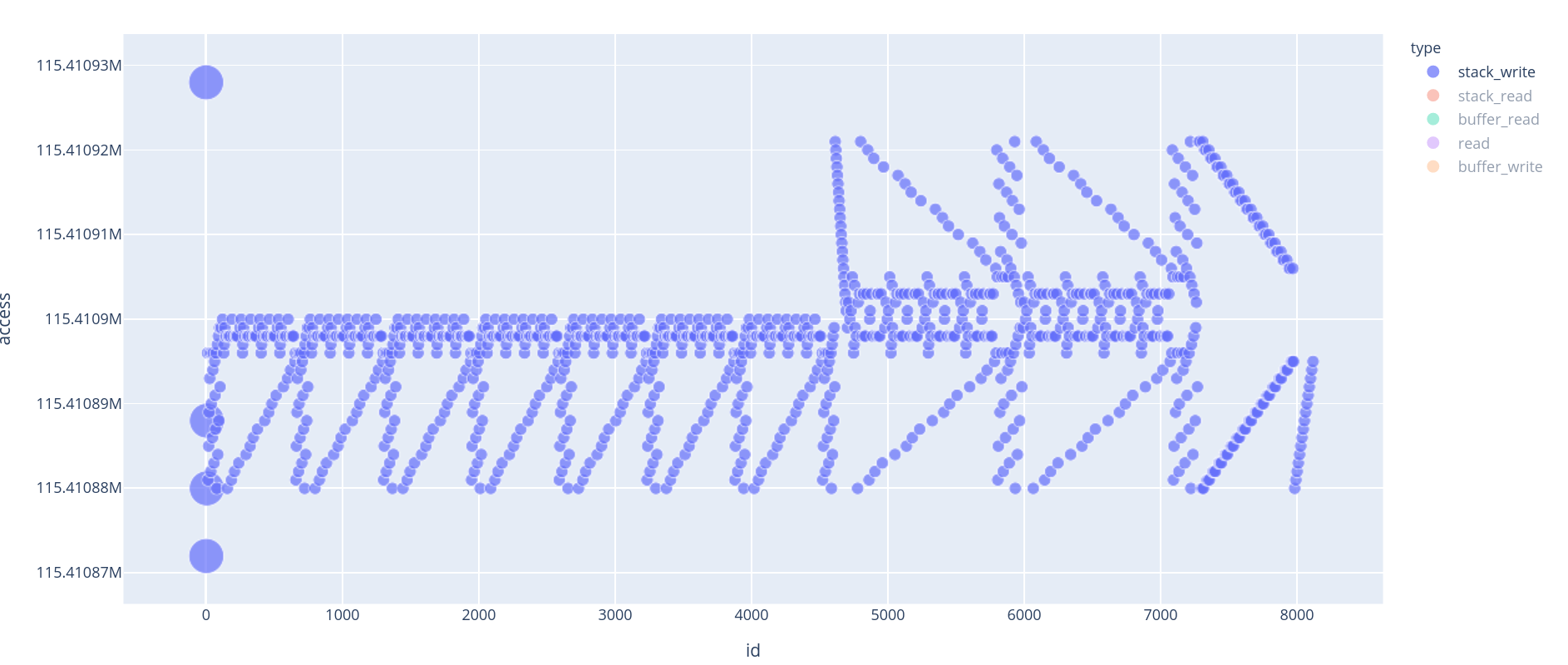Stack write accesses give information about the
underlying algorithm
So we are facing an AES-128, perfect for the collision-based attack we just built. We need a few things to be able to run this attack:
- Observe the state of AES at the end of round 0
- Generate collisions
So how can we get access to the state at the end of round 0? First of all, we need to know where the state is located in memory.
If you were to look a bit closer at how data are accessed, you would see packs of 4 bytes being accessed almost sequentially.
Moreover, if you remember the encrypt function, it begins with a memcpy, copying the input bytes to a static buffer on the stack. This is the state initialization. So we know where the state is:
// s[0:16] is the state uint8_t s[42]; [...] memcpy(s, buffer, 16);
Now, if we want to know where the end of round 0 happens, we can use the previous visualization to have an approximation of the end of the round. It happens around id 600/650 ~ (see the capture below, zoomed on the first 3 rounds of AES).
Note: The 2 big (8-byte-write) stack_write at the beginning are in fact the memcpy that has been inlined.
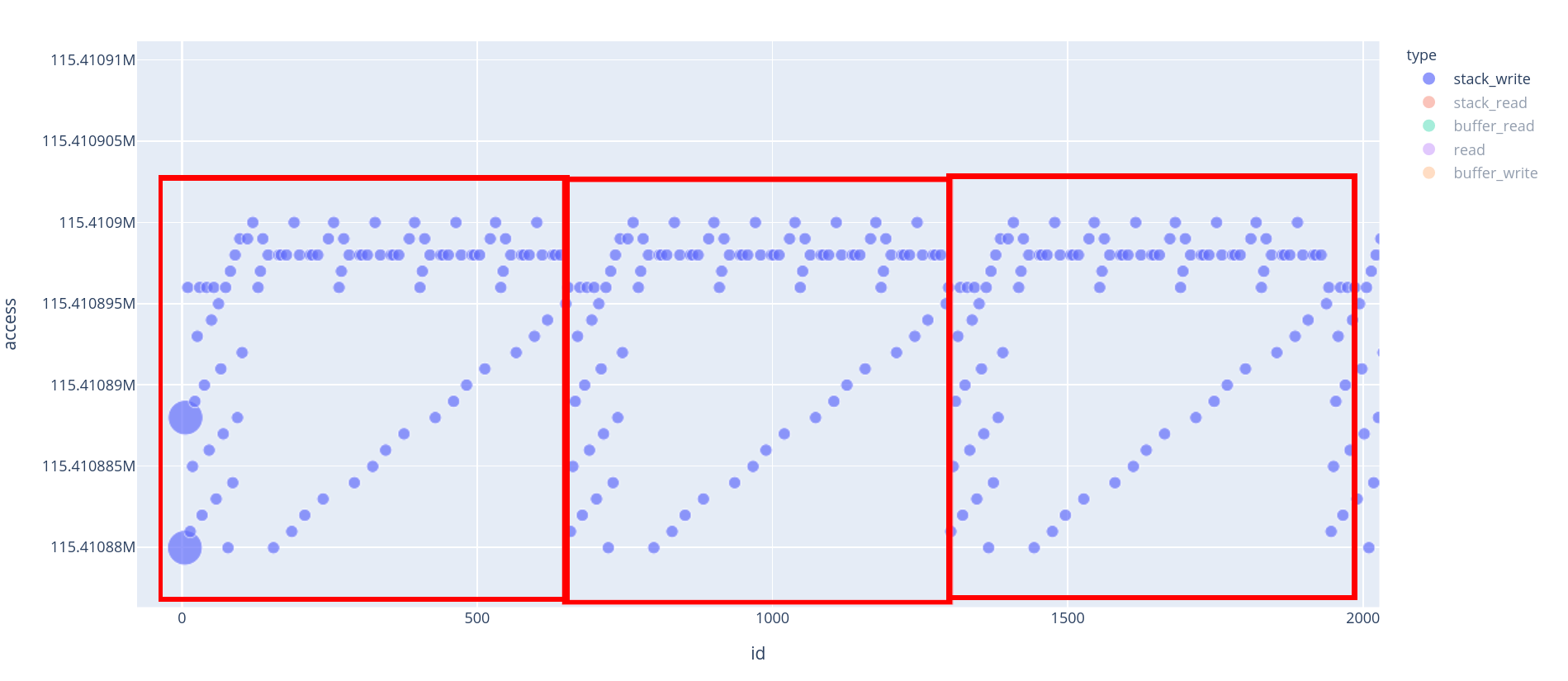Zoom on the first 3 rounds of AES
We can see that at every round, each byte of the state is being written twice, before we move on to the next round. This basic heuristic is enough for us to determine where the round 0 ends.
Let’s modify a bit the callback and the instrumentation to get those data. We can retrieve the address of the state by looking at the first accesses of size 8 (we can see the memcpy reading our input buffer, and then writing it to the stack).
memory_accesses["accesses"][3:7]
[{'id': 3, 'access': 52139832, 'type': 'buffer_read', 'size': 8},
{'id': 4, 'access': 52139824, 'type': 'buffer_read', 'size': 8},
{'id': 5, 'access': 140224210382672, 'type': 'stack_write', 'size': 8},
{'id': 6, 'access': 140224210382680, 'type': 'stack_write', 'size': 8}]
The start of the buffer is at rsp - 0xc0, we will use this to detect the end of round 0 as demonstrated in the snippet below:
Note: Since we need only the state at the end of round 0, we can stop the execution of the function after the first round and move on. This speeds up the process a bit.
# Callback, called on every memory access def mem_cbk(vm, gpr, fpr, cb_data): # State address on the stack state_addr = cb_data["stack"] - 0xc0 accesses = cb_data["accesses"] byte_access = cb_data["byte_access"] # Keep a counter on the number of memory accesses ctr = cb_data["ctr"] memaccess = vm.getInstMemoryAccess() for acc in memaccess: # We are interested in accesses to the state if acc.accessAddress not in range(state_addr, state_addr+16): continue rw_type = ["write", "read"][not (acc.type & pyqbdi.MEMORY_WRITE)] # We are interested only in writes if rw_type != "write": continue # We are interested in 1 byte accesses (to filter out the memcpy) if acc.size != 1: continue # Store information about the memory access accesses.append({"id":ctr, "access": acc.accessAddress, "type":rw_type, "size":acc.size}) cb_data["ctr"] += 1 # Record the number of time each byte is being written byte_access[acc.accessAddress - state_addr] += 1 # If each byte has been accessed twice, we stop the execution if byte_access == [2]*16: # Dump the intermediate state cb_data["state_e0"] = pyqbdi.readMemory(state_addr, 16) return pyqbdi.STOP return pyqbdi.CONTINUE
def main(): encrypt_ptr = load_wb() vm = instanciate_vm(encrypt_ptr) buffer_ptr = pyqbdi.allocateMemory(16) # Add memory callback state = vm.getGPRState() cb_data = {"accesses":[], "ctr":0, "stack": state.rsp, "byte_access":[0]*16, "state_e0": None} vm.addMemAccessCB(pyqbdi.MEMORY_READ_WRITE, mem_cbk, cb_data) encrypt(vm, encrypt_ptr, buffer_ptr, [0]*16) print("State at the end of round 0 : ", list(cb_data["state_e0"])) return cb_data memory_accesses = main()
State at the end of round 0 : [45, 127, 179, 60, 184, 146, 58, 29, 6, 243, 40, 93, 17, 113, 101, 61]
Generating collisions
We can now observe the state at the end of round 0, so we can get started with the collision attack. First we need to generate a few collisions. To optimize a bit the algorithm, we will tweak the way we are generating traces. If you remember, we break 2 bytes of key, and then the 2 remaining bytes. We have to do this 4 times, for the 4 independent blocks of AES.
Since the operations are independent, we can attack the 4 blocks at the same time, so instead of modifying only 2 bytes per plaintext, we will modify \(4 \times 2\) bytes, and observe collisions independently on each block of the output. This helps getting collisions for half of the key; it then needs to be done for the other half of the key.
Note: All previous examples were executed with "input_bytes":[0, 5, 10, 15]. This was handy because you do not need to take care of endinanness for the test as bytes are mirrored. For the following, we need to take care of it, so don’t be troubled by the key = key[::-1] and input_data[::-1] that are here to properly represent the endianness.
RELATIONSHIP = [ {"affected_bytes":[0,1,2,3], "input_bytes":[0, 5, 10, 15]}, {"affected_bytes":[4,5,6,7], "input_bytes":[1, 6, 11, 12]}, {"affected_bytes":[8,9,10,11], "input_bytes":[2, 7, 8, 13]}, {"affected_bytes":[12,13,14,15], "input_bytes":[3, 4, 9, 14]}, ] import random def generate_traces(n_traces, half): encrypt_ptr = load_wb() vm = instanciate_vm(encrypt_ptr) buffer_ptr = pyqbdi.allocateMemory(16) # Add memory callback state = vm.getGPRState() cb_data = {"accesses":[], "ctr":0, "stack": state.rsp, "byte_access":[0]*16, "state_e0": None} vm.addMemAccessCB(pyqbdi.MEMORY_READ_WRITE, mem_cbk, cb_data) traces = [] for i in range(n_traces): input_data = [0]*16 for r in RELATIONSHIP: input_data[r["input_bytes"][2*half]] = random.randint(0,255) input_data[r["input_bytes"][(2*half) + 1]] = random.randint(0,255) input_data = input_data[::-1] encrypt(vm, encrypt_ptr, buffer_ptr, input_data) state_e0 = list(cb_data["state_e0"]) traces.append({'input_data':input_data, "state_e0":state_e0}) # reset data cb_data["accesses"] = [] ; cb_data["ctr"] = 0 cb_data["byte_access"] = [0]*16 ; cb_data["state_e0"] = None return traces # We need two sets of traces,to break 2 bytes per block, then the 2 remaining bytes. traces_half0 = generate_traces(64, 0) traces_half1 = generate_traces(64, 1)
So we generated two sets of traces. The first set of traces is made to break the first half of the key (in the previous examples \(k_0\) and \(k_5\)) for the 4 blocks of AES. While the second set of traces will be used to break the remaining bytes of the key (\(k_{10}\) and \(k_{15}\)).
Now we need to look for collisions in those traces. We are looking for collisions by checking if two plaintexts give an identical output byte.
Note: In the example, we are always looking at a single byte target_byte. To be more efficient, and minimize the number of required traces, one could check for collisions on each of the affected bytes. However to keep things simple, we will always be looking for collisions on the same output byte for each block.
# Look for collisions in traces def find_collisions(traces, target_byte): collisions = [] for i, trace in enumerate(traces): for pair in traces[i+1:]: if trace['state_e0'][target_byte] == pair['state_e0'][target_byte]: collisions.append({'P0':trace, 'P1':pair}) return collisions def is_colliding(p0, p1, key, target_byte): s0 = aes_round_0(p0, key) s1 = aes_round_0(p1, key) if s0[target_byte] == s1[target_byte]: return True # Find all keys generating a collision for a given pair of input def find_colliding_keys(p0, p1, relationship, half, target_byte): # Iterate over all the key space, to find one key that generate a collision # on a plain AES. colliding_keys = [] for i in range(256): for j in range(256): key = [0]*16 key[relationship['input_bytes'][2*half]] = i key[relationship['input_bytes'][(2*half) + 1]] = j key = key[::-1] if is_colliding(p0, p1, key, target_byte): colliding_keys.append(key) return colliding_keys
Once we managed to recover a few pairs of colliding plaintexts, we can start recovering the key. The algorithm is quite simple, we take a first pair of plaintexts, compute all the potential keys and keep the ones generating a collision. We then test those keys against a new pair of plaintexts, and keep only the keys that also generated a collision for this pair. (And we go on, until a single key is left.)
Below is the attack demonstrated, and the recovery of the whitebox key:
def break_subkey(traces, relationship, half): target_byte = relationship["affected_bytes"][0] collisions = find_collisions(traces, target_byte) pk = [] for i in collisions: # Compute all the keys for the first pair of plaintexts if not pk: pk = find_colliding_keys(i['P0']['input_data'], i['P1']['input_data'], relationship, half, target_byte) # Test those keys against the other pairs and keep only the colliding ones else: left_keys = [] for k in pk: if is_colliding(i['P0']['input_data'], i['P1']['input_data'], k, target_byte): left_keys.append(k) pk = left_keys return pk.pop() final_key = [0]*16 for block in range(4): print(F"Breaking half-0 of block {block}") subkey_0 = break_subkey(traces_half0, RELATIONSHIP[block], 0) print(F"Subkey found is {subkey_0}") print(F"Breaking half-1 of block {block}") subkey_1 = break_subkey(traces_half1, RELATIONSHIP[block], 1) print(F"Subkey found is {subkey_1}") # subkeys are null except on bytes of interest, so we can XOR them final_key = [final_key[i] ^ subkey_0[i] for i in range(16)] final_key = [final_key[i] ^ subkey_1[i] for i in range(16)] print("-"*80) print(F"Final key recovered : { bytes(final_key)}")
Breaking half-0 of block 0
Subkey found is [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 115, 0, 0, 0, 0, 125]
Breaking half-1 of block 0
Subkey found is [71, 0, 0, 0, 0, 65, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
--------------------------------------------------------------------------------
Breaking half-0 of block 1
Subkey found is [0, 0, 0, 0, 0, 0, 0, 0, 0, 105, 0, 0, 0, 0, 78, 0]
Breaking half-1 of block 1
Subkey found is [0, 0, 0, 57, 123, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
--------------------------------------------------------------------------------
Breaking half-0 of block 2
Subkey found is [0, 0, 0, 0, 0, 0, 0, 0, 32, 0, 0, 0, 0, 85, 0, 0]
Breaking half-1 of block 2
Subkey found is [0, 0, 49, 0, 0, 0, 0, 83, 0, 0, 0, 0, 0, 0, 0, 0]
--------------------------------------------------------------------------------
Breaking half-0 of block 3
Subkey found is [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 32, 70, 0, 0, 0]
Breaking half-1 of block 3
Subkey found is [0, 72, 0, 0, 0, 0, 69, 0, 0, 0, 0, 0, 0, 0, 0, 0]
--------------------------------------------------------------------------------
Final key recovered : b'GH19{AES is FUN}'
The key we recovered is GH19{AES is FUN}, which seems like the good one! We tested this attack against a few other whiteboxes, and it worked pretty well. Other attacks like DCA and DFA on round 8 (because the last rounds are protected) would also have worked here and are generally really efficient (see [10] and [11] for the attacks).
There are a few differences between all those attacks, DCA is based on a statistical approach, so it might fail, on one or two key bytes, requiring a quick brute force or a second run to succeed. DFA attacks require to fault the good section of the tables in order to be efficient.
With this collision-based attack, we just have to target the input that we control, and since there are no statistics involved, the success rate is 100%.
However, I am not saying this attack is better (it is not). It has its downside, for instance, you need to be able to observe the end of round 0, which might not always be easy if the whitebox is obfuscated (where it is easier with DFA, since you are observing the output of AES). Yet, this attack is interesting, because it does not require a lot of mathematical, cryptographic or reversing background to get it working.
And like for DFA and DCA, a whitebox can be built to be protected against this attack. For instance, I believe that large encodings would render the attack unusable (I haven't tested it though). Also note that obfuscation can also be another layer of protection against this kind of attacks.
Conclusion
This post was mostly written to share my thought process and journey from zero-knowledge about whiteboxes, to breaking a few of them (among which the GreHack2019 whitebox [10]). Hopefully, it will help some of you to get into the subject, that in the end, is not so unreachable. Also, it puts the light on another usage of QBDI for cryptanalysis, which is one of the many usages of DBI frameworks.
Sadly, for the hardcore reversers or equation-lovers, you might not have found what you were looking for, but feel free to send us a custom whitebox, that I would be happy to attack and write about :).
Sorry for the long post, here is a potato: 🥔