day9 的输入是:
7,1 11,1 11,7 9,7 9,5 2,5 2,3 7,3
这是一系列的坐标点,例如 7,1 表示的是 x=7,y=1 的一个位置,用 # 标记这些位置,可以得到下面的图:
.............. .......#...#.. .............. ..#....#...... .............. ..#......#.... .............. .........#.#.. ..............
part1 的问题是,用任意两个点作为对角,形成一个矩形,当前的输入中,可以形成的矩形面积最大是多少。
例如 2,5 和 9,7 可以形成这样的矩形:
.............. .......#...#.. .............. ..#....#...... .............. ..OOOOOOOO.... ..OOOOOOOO.... ..OOOOOOOO.#.. ..............
面积是 24。
part1 的思路挺简单的,遍历所有的坐标,任意两个坐标组合到一起,计算形成的矩形面积,返回最大的面积即可。
part2 的问题是,现在的坐标会形成一个封闭的区域,变成这样:
.............. .......#XXX#.. .......XXXXX.. ..#XXXX#XXXX.. ..XXXXXXXXXX.. ..#XXXXXX#XX.. .........XXX.. .........#X#.. ..............
还是同样的输入,还是任意选择两个对角的点,求可以形成的最大矩形面积。但是新增了一个约束条件,形成的矩形,只能由 # 或者 X 组成,不能包含 . ,也就是说对角形成的矩形,必须在这个封闭区域的内部。
思考了一下,如果要求形成的矩形在封闭区域内部,意味着矩形的四个顶点也应该在封闭区域内,不能超出封闭区域。# 对应的坐标点肯定在轮廓的边上,我只要判断矩形的另外两个对角点在不在封闭区域内不就好了?
但是怎么判断一个点是否在一个封闭轮廓内呢?对此我也没什么头绪,求助了 LLM,了解到可以用 点射法。
点射法,也叫射线投射算法(Ray casting algorithm),它基于一个观察:如果一个点沿着一条射线从无穷远移动到探测点,并且它穿过了多边形的边界(可能多次),那么它会交替地从外部进入内部,然后从内部进入外部,依此类推。因此,每两次「越界(border crossing)」后,移动点就会回到外部。
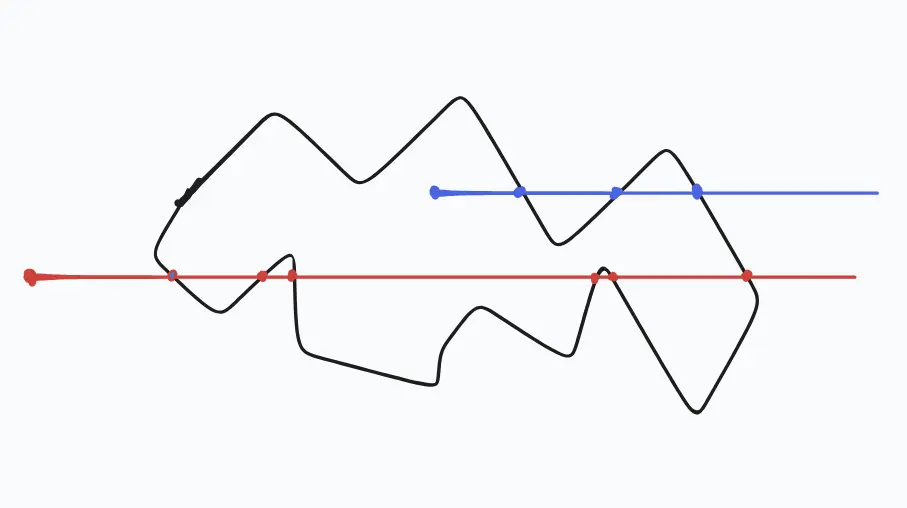
于是尝试了点射法(顺便复习了一下怎么构造直线方程),遍历每一个组成矩形的顶点,看看它们是否在封闭区域中,过滤出符合条件的矩形、计算面积、找到最大的矩形面积,兴高采烈地输入答案,结果是错的。_(:3 」∠)_
估计是漏了什么条件没有考虑到,想了好久也没想出来,就去翻了 reddit,从评论里我意识到了一种可能 ⸺ 封闭区域可能是凹进去的!
示例让我以为实际输入也是类似的图案,但 实际图案 可能是凹的,例如:
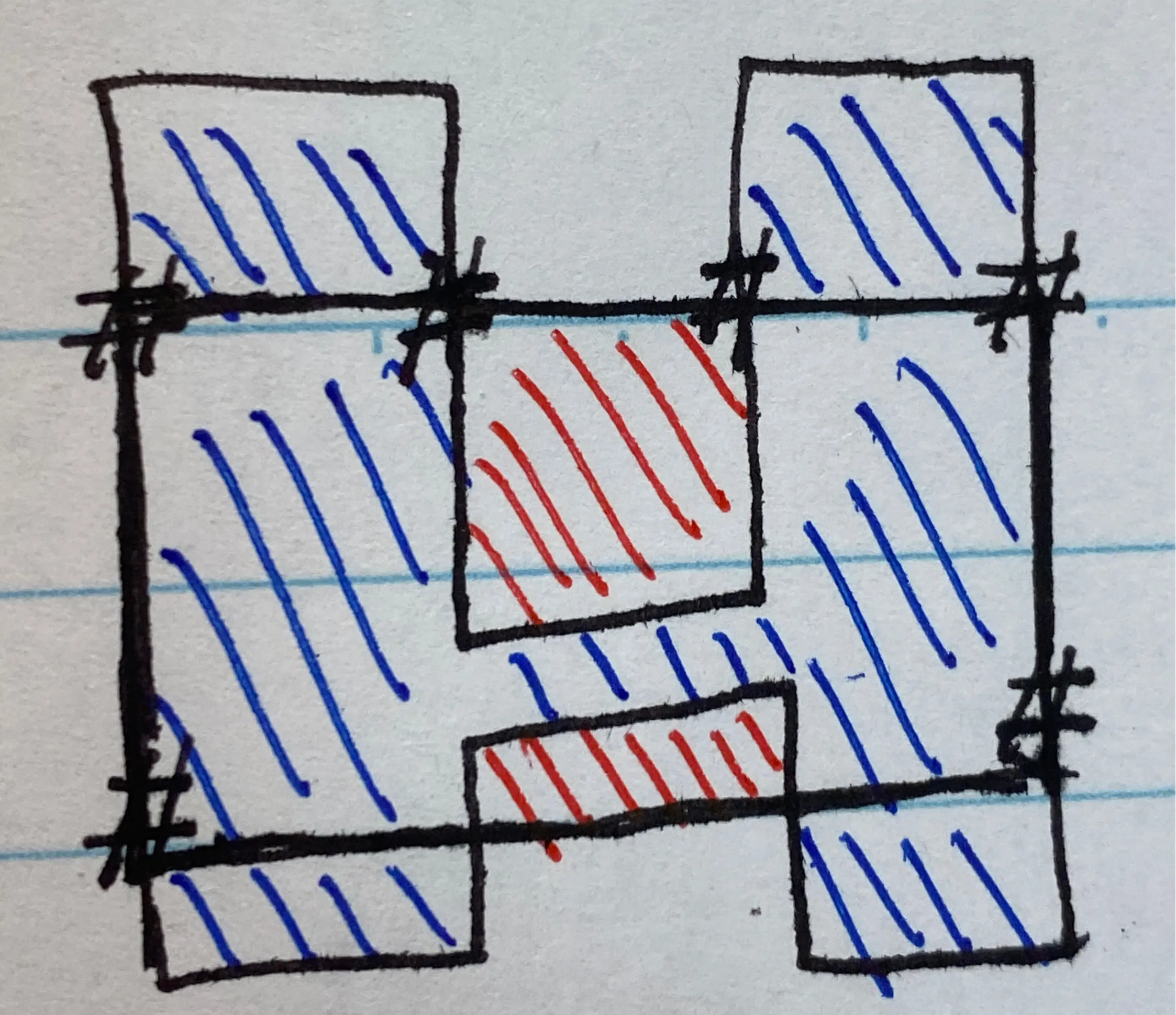
如 图 2 所示,尽管选取的矩形四个顶点都在封闭区域内,但是由于封闭区域是凹的,封闭区域会穿透矩形,导致矩形有一部分区域(红色部分)不在封闭区域中,这样的矩形是不符合 part2 的要求的。
怎么判断这种情况呢?可以通过判断矩形的每一条边是否和封闭区域的边相交,如果没有相交,说明封闭区域没有穿透矩形,这样的矩形就是满足条件的;如果相交了(如 图 2),说明封闭区域穿透了矩形,这样的矩形是不满足条件的。
因此,解决 part2,需要:
- 遍历所有可能的矩形的四个顶点,使用点射法,判断顶点是否都在封闭区域内
- 遍历所有可能的矩形的四条边,判断是否和封闭区域的边相交
代码写起来边界条件比较多,判断也很多,最后找 LLM 帮忙写了一个版本(偷懒了)。这个版本运行了将近一分钟才得到结果 _(:3 」∠)_。我自己写的话,估计要写很久,调试很久才行。
这次是练习 python,python 中有很多有用的库,其中 shapely 就很擅长处理平面几何的问题。利用其中的 Polygon ,传入一组顺序的坐标点,就可以构造得到一个多边形;Polygon 生成的对象上有一个 within 方法,可以判断包含关系,利用它就可以轻易判断矩形是否在封闭区域内了。
相关的代码可以看看 Yordi Verkroost 的 Advent of Code 2025 - Day 9,比用点射法来得要方便很多,也不容易出错。
day9 的 part2 对我来说还挺难的,没什么头绪,挣扎了很久。不过也因此了解了点射法,了解了 shapely,也算有所收获。
