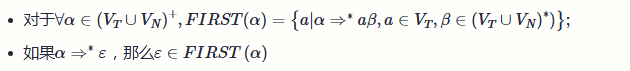LL(1) 算法
一、LL(1) 文法介绍第一个L代表 分析时从左向右扫描第二个L代表分析过程将最左推导 1 代表只需要向右看一个符号二、FIRST 集合FIRST(N) 2025-1-4 16:43:33 Author: www.o2oxy.cn(查看原文) 阅读量:3 收藏
一、LL(1) 文法介绍第一个L代表 分析时从左向右扫描第二个L代表分析过程将最左推导 1 代表只需要向右看一个符号二、FIRST 集合FIRST(N) 2025-1-4 16:43:33 Author: www.o2oxy.cn(查看原文) 阅读量:3 收藏
一、LL(1) 文法介绍
第一个L代表 分析时从左向右扫描
第二个L代表分析过程将最左推导
1 代表只需要向右看一个符号
二、FIRST 集合
FIRST(N) = 从非终结符N开始推导的出句子开头的所有可能终结符号集合
公式:
简单理解为:就是找非终结符
对 N-> a ....
FIRST(N) U ={a}
如果把a换成一个变量M M代表终结符例如a 或者b 或者 c 或者n
对 N-> M ....
FIRST(N) U ={M}
一个简单的例子
例如
S -> N
N --> A C
A -->| b
C --> a
那么FIRST(A)={b,a}
2.1 FIRST集的不动点算法
伪代码
foreach (nonterminal N)
FIRST(N) = {}
while (some set is changing) // 某一些符号的集合还在增大
foreach (production p: N -> β1 ... βn)
foreach (βi from β1 upto βn)
if (β1 == a ...) // 最右推导 β1
FIRST(N) U= {a}
break
if (β1 == M ...)
FIRST(N) U= FIRST(M)
if(M is not in NULLABLE)
break
例如文法如下:
0:S -> N V N 1 : N-> s 2 : | t 3 : | g 4 : | w 5 : V -> e 6: | d
得到的结果为 0-3 是循环次数
| N\FIRST | 0 | 1 | 2 | 3 |
| S | {} | {} | {s,t,g,w} | {s,t,g,w} |
| N | {} | {s,t,g,w} | {s,t,g,w} | {s,t,g,w} |
| V | {} | {e,d} | {e,d} | {e,d} |
简单的说明:
第一轮 N加到S中 因为两个都是空的集合那么 结果为{}
N 为 {s,t,g,w}
V 为 {e,d}S
第二轮 N 加到S中 因为N是{s,t,g,w} 那么结果为{s,t,g,w}
N 没有发生变化
V 没有发生变化
第三轮 S的第一次和第二次发生了变化触发合并 但是都是{s,t,g,w} 那么合并的数据还是{s,t,g,w}
N 没有发生变化
V 没有发生变化
文章来源: https://www.o2oxy.cn/4342.html
如有侵权请联系:admin#unsafe.sh
如有侵权请联系:admin#unsafe.sh