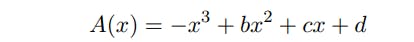
Authors:
(1) Agustin Moreno;
(2) Francesco Ruscelli.
Table of Links
- Abstract
- Introduction
- Preliminaries
- The B-signature
- GIT sequence: low dimensions
- GIT sequence: arbitrary dimension
- Appendix A. Stability, the Krein–Moser theorem, and refinements and References
5. GIT sequence: arbitrary dimension


Among these components, there is a special one, the stable component, which corresponds to stable periodic orbits. We will show that its combinatorics is governed by a quotient of the associahedron.
5.1. Some real algebraic geometry. Consider the space of monic polynomials with real coefficients and of degree n, i.e. of the form

Recall that the discriminant of a polynomial is defined as the expression



Example 5.1. For the case n = 3, every polynomial

can be transformed via the change of variables y = x − b/3 to a polynomial with no degree 2 term (a depressed cubic polynomial), i.e. of the form




Remark 5.2. Note that if there are complex quadruples in the spectrum, then the Bblock always has at least one summand of the form diag(1, −1). Viewed as a bilinear form, this matrix always has mixed signature. As signatures behave continuously in the space of non-degenerate bilinear forms, this implies that the corresponding quadruple cannot be connected to a hyperbolic or elliptic pair of multiplicity two of definite signature, while fixing the remaining eigenvalues. This is the main observation that implies the Krein– Moser theorem, cf. Appendix A. This is also what implies its refinement for symmetric orbits (Theorem A).


Nonregular cases. The nonregular cases can be dealt with similarly, although the combinatorics gets more involved. Indeed, assume that A has real eigenvalues

where we also allow ±1 as an eigenvalue, and complex eigenvalues

We denote the multiplicities by


The associahedron. The boundary combinatorics of the stable region can be alternatively encoded as follows. We identify the simple eigenvalues

indicates that the eigenvalues νj and νj+1 come together into a multiplicity two eigenvalue, and so corresponds to the contraction of multiplicities given by
(1, . . . , 1) 7→ (1, . . . , 2, . . . , 1).
Similarly, a further parenthesis
−1ν1 . . . νj−1{νj , νj+1} . . . νl1 7→ −1ν1 . . . {νj−1, νj , νj+1} . . . νl1
indicates that the eigenvalue νj−1 came together with the previous multiplicity two eigenvalue into a multiplicity three eigenvalue, and so corresponds to the contraction
(1, . . . , 1, 2, . . . , 1) 7→ (1, . . . , 3, . . . , 1).
This construction iterates in the obvious way. Here we also allow eigenvalues to come together with ±1, i.e. {−1, ν1}ν2{ν3, ν4, 1} is a valid expression. Note that we use the bracket notation to indicate that the order of the elements in the bracket is irrelevant. Iterating this construction results in a poset of strings (in which all open brackets are accompanied by a corresponding closed one, and there are no nested brackets), and where two strings a, b satisfy a ≤ b if b is obtained by a sequence of brackets operations from a. This poset then encodes the boundary combinatorics of the stable region, by construction.

Now, the above is intimately related to the operation of taking parenthesis operations

and iterating them, similarly as above, e.g. as

and so on, where now a valid expression is for instance ((−1ν1)ν2)ν3(ν41). The bracket is then the result of removing all interior parenthesis in an expression, i.e. symbolically via (. . .(. . .). . .) 7→ (. . .), and modding out by the action of the corresponding permutation group (i.e. acting on the number of elements inside the bracket), symbolically via

For instance, the above expression becomes {−1, ν1, ν2}ν3{ν4, 1}, where now the order of the elements inside the bracket is irrelevant.
But the combinatorics of expressions with parenthesis is governed by a very-well known polytope, called the associahedron. This is the (m − 2)-dimensional convex polytope Km in which each vertex corresponds to a way of correctly inserting opening and closing parentheses in a string of m letters (meaning that it uniquely determines the order of the product operations), and the edges correspond to single application of the associativity rule. This can also be viewed as a poset, when the arrow indicates that the parentheses have been moved to the right (this is the Tamari lattice). Moreover, one can also label the edges


In order to obtain the stable region from the associahedron, we observe that many labels in the latter are actually equivalent when written with the bracket notation. We then conclude:

In other words, the stable region is homeomorphic to a quotient of the associahedron, where we identify those strata whose label become equivalent when written in the bracket notation. The low dimensional cases (n = 1, 2, 3) are depicted in Figures 6 and 7.





如有侵权请联系:admin#unsafe.sh