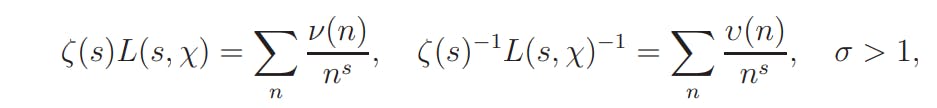
2024-6-2 23:11:49 Author: hackernoon.com(查看原文) 阅读量:0 收藏
Author:
(1) Yitang Zhang.
Table of Links
- Abstract & Introduction
- Notation and outline of the proof
- The set Ψ1
- Zeros of L(s, ψ)L(s, χψ) in Ω
- Some analytic lemmas
- Approximate formula for L(s, ψ)
- Mean value formula I
- Evaluation of Ξ11
- Evaluation of Ξ12
- Proof of Proposition 2.4
- Proof of Proposition 2.6
- Evaluation of Ξ15
- Approximation to Ξ14
- Mean value formula II
- Evaluation of Φ1
- Evaluation of Φ2
- Evaluation of Φ3
- Proof of Proposition 2.5
Appendix A. Some Euler products
Appendix B. Some arithmetic sums
3. The set Ψ1
Let ν(n) and υ(n) be given by

respectively. It is easy to see that

Lemma 3.1. Assume (A) holds. Then

Proof. Let

which has the Euler product representation

For σ ≥ σ0 > 0, by checking the cases χ(p) = ±1 and χ(p) = 0 respectively, it can be seen that

and

the implied constant depending on σ0. Thus φ(s) is analytic for σ > 1/2 and it satisfies

for σ ≥ σ1 > 1/2, the implied constant depending on σ1. The left side of (3.2) is


Lemma 3.2. Assume (A) holds. Then we have

Proof. As the situation is analogous to Lemma 3.1 we give a sketch only. It can be verified that the function

is analytic for σ > 1/2 and it satisfies

for σ ≥ σ1 > 1/2, the implies constant depending on σ1. Also, one can verify that

This completes the proof.
Lemma 3.3. For any s and any complex numbers c(n) we have

and

Proof. The first assertion follows by the orthogonality relation; the second assertion follows by the large sieve inequality.
Let

By (3.1) we may write

By Cauchy’s inequality and the first assertion of Lemma 3.3 we obtain

Thus we conclude
Lemma 3.4. The inequality

Write

Assume that (A) holds. By Cauchy’s inequality, the second assertion of Lemma 3.2 and Lemma 3.1,

Thus we conclude
Lemma 3.5 Assume that (A) holds. The inequality

Let

Assume that (A) holds. By Cauchy’s inequality, the first assertion of Lemma 3.2 and Lemma 3.1,

Thus we conclude
Lemma 3.6. Assume that (A) holds. The inequality

We are now in a position to give the definition of Ψ1: Let Ψ1 be the subset of Ψ such that ψ ∈ Ψ1 if and only if the inequalities (3.4), (3.5) and (3.6) simultaneously hold.
Proposition 2.1 follows from Lemma 3.4, 3.5 and 3.6 immediately.
如有侵权请联系:admin#unsafe.sh