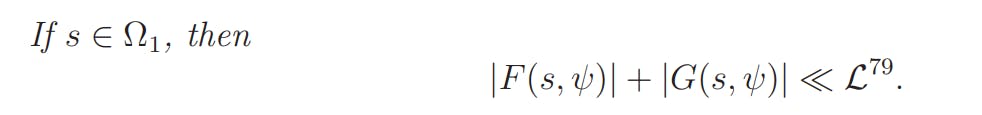
2024-6-2 23:11:58 Author: hackernoon.com(查看原文) 阅读量:0 收藏
Author:
(1) Yitang Zhang.
Table of Links
- Abstract & Introduction
- Notation and outline of the proof
- The set Ψ1
- Zeros of L(s, ψ)L(s, χψ) in Ω
- Some analytic lemmas
- Approximate formula for L(s, ψ)
- Mean value formula I
- Evaluation of Ξ11
- Evaluation of Ξ12
- Proof of Proposition 2.4
- Proof of Proposition 2.6
- Evaluation of Ξ15
- Approximation to Ξ14
- Mean value formula II
- Evaluation of Φ1
- Evaluation of Φ2
- Evaluation of Φ3
- Proof of Proposition 2.5
Appendix A. Some Euler products
Appendix B. Some arithmetic sums
4. Zeros of L(s, ψ)L(s, χψ) in Ω
In this section we prove Proposition 2.2. We henceforth assume that ψ(mod p) ∈ Ψ1. This assumption will not be repeated in the statements of Lemma 4.1-4.8.
We begin by proving some consequences of the inequalities (3.4)-(3.6).
Lemma 4.1. Let


Proof. By the Stieltjes integral we may write

Hence, by partial integration,

For G(s, ψ) an entirely analogous bound is valid. The result now follows by (3.4).
Lemma 4.2. If s ∈ Ω1, then

Proof. We have

Thus, similar to (4.2), by partial integration we obtain

Lemma 4.3. Let

We proceed to establish an approximate formula for L(s, ψ)L(s, χψ). For this purpose we first introduce a weight g(x) that will find application at various places. Let

with

We may write

Since

it follows, by changing the order of integration, that

Thus the function g(x) is increasing and it satisfies 0 < g(x) < 1. Further we have

Note that χψ is a primitive character (modDp). Write

so that


By (2.4) with θ = ψ and θ = χψ we have

This yields, by Stirling’s formula,

and

Lemma 4.4. Let

If s ∈ Ω3, then

Proof. By the residue theorem,

By (4.2) and (4.3),

By (3.5) and partial summation, the second sum on the right side above is

On the other hand, by the functional equation, for u = −σ − 1/2,



and

To prove (4.7) we move the contour of integration to the vertical segments

and to the two connecting horizontal segments

By a trivial bound for ω1(w), (4.5) and the residue theorem we obtain (4.7).
To prove (4.8) we move the contour of integration to the vertical segments

and to the two connecting horizontal segments

By a trivial bound for ω1(w) and (4.5) we see that the left side of (4.8) is

with s ∗ = 1 + α − s¯. By partial integration,

The estimate (4.9) follows by moving the contour of integration to the vertical segments
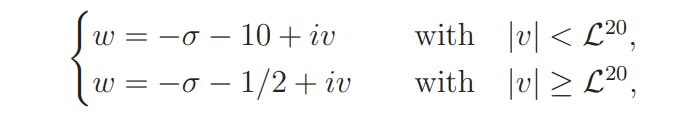
and to the two connecting horizontal segments

and applying (4.5) and trivial bounds for ω1(w) and the involved sum.
In order to prove Proposition 2.2, it is appropriate to deal with the function

By Lemma 4.2, A(s, ψ) is analytic and it has the same zeros as L(s, ψ)L(s, ψχ) in Ω1. Further, for s ∈ Ω1, we have

by Lemma 4.1 and 4.2. This together with Lemma 4.4 implies that

for s ∈ Ω3, where

The proof of Proposition 2.2 is reduced to proving three lemmas as follows.
Lemma 4.5. If

then

Proof. We discuss in two cases.

By Lemma 4.2 and trivial estimation,

Hence, by (4.5),

The result now follows by (4.10).

Since |B(1/2 + it, ψ)| = 1, it follows that

Hence, by (4.10),

Lemma 4.6. Suppose ρ = β + iγ is a zero of A(s, ψ) satisfying

Proof. It suffices to show that the function A(1/2 + iγ + w, ψ) has exactly one zero inside the circle |w| = α(1 − c ′αL), counted with multiplicity. By the Rouch´e theorem, this can be reduced to proving that



In either case (4.16) holds.
Lemma 4.5 and 4.6 together imply the assertions (i) and (ii) of Proposition 2.2. It is also proved that the gap between any distinct zeros of A(s, ψ) in Ω is > α(1 − c ′αL). To complete the proof of the gap assertion (iii), it now suffices to prove

Proof. In a way similar to the proof of Lemma 4.6, it is direct to verify that

We conclude this section by giving a result which is implied in the proof of Proposition 2.2.
Lemma 4.8. Assume that ρ is a zero of L(s, ψ)L(s, χψ) in Ω. Then we have

Proof. It follows from Lemma 4.4 that

如有侵权请联系:admin#unsafe.sh