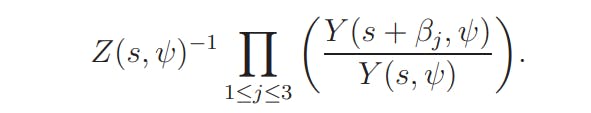
2024-6-2 23:12:7 Author: hackernoon.com(查看原文) 阅读量:0 收藏
Author:
(1) Yitang Zhang.
Table of Links
- Abstract & Introduction
- Notation and outline of the proof
- The set Ψ1
- Zeros of L(s, ψ)L(s, χψ) in Ω
- Some analytic lemmas
- Approximate formula for L(s, ψ)
- Mean value formula I
- Evaluation of Ξ11
- Evaluation of Ξ12
- Proof of Proposition 2.4
- Proof of Proposition 2.6
- Evaluation of Ξ15
- Approximation to Ξ14
- Mean value formula II
- Evaluation of Φ1
- Evaluation of Φ2
- Evaluation of Φ3
- Proof of Proposition 2.5
Appendix A. Some Euler products
Appendix B. Some arithmetic sums
5. Some analytic lemmas


The proofs of (5.3) and (5.4) are similar.
Lemma 5.2. Let ψ and s be as in Lemma 5.1. Then

Proof. The left side is

By (2.6) and the Stirling formula, for |w| < 5α,

Hence, for 1 ≤ j ≤ 3,

The result now follows since

Recall that ϑ(s) and ω(s) are given by (2.3) and (2.15) respectively. It is known that

For t > 1 we have

where

Let

and

Note that


Proof. By the Mellin transform (see [1], Lemma 2) we have


with

By the relation

and Cauchy’s theorem, the proof of (5.8) is reduced to showing that

for 1 ≤ j ≤ 5, where Lj denote the segments


This yields (5.12) with j = 3 .
As a consequence of Lemma 5.3, the Mellin transform

is analytic for σ > 0.
Lemma 5.4. (i). If 1/2 ≤ σ ≤ 2, then

(ii). If |s − 1| < 10α, then

Proof. (i). Using partial integration twice we obtain

By (5.10) we have

Thus some upper bounds for ∆′′(x) analogous to Lemma 5.3 can be obtained, and (i) follows.

Throughout the rest of this paper we assume that (A) holds. This assumption will not be repeated in the statements of the lemmas and propositions in the sequel.
The next two lemmas are weaker forms of the Deuring-Heillbronn Phenomenon.


Lemma 5.7. We have

Proof. The right side of the equality

Lemma 5.8. If

then

where

Proof. This follows from the relation

(A) and a simple bound for L ′′(w, χ).

Proof. It is known that


so that

By (9.1) and the condition |s − ρ| ≫ α for any ρ,

so that

Further, by (5.16) and Proposition 2.2 (iii),

Combining theses estimates we obtain the result. In the case σ < 1/2 the proof is analogous.
如有侵权请联系:admin#unsafe.sh