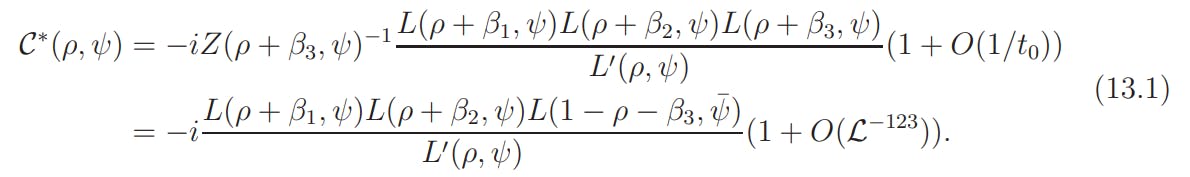
Discrete Mean Estimates and the Landau-Siegel Zero: Approximation to Ξ14
2024-6-2 23:13:37 Author: hackernoon.com(查看原文) 阅读量:3 收藏
2024-6-2 23:13:37 Author: hackernoon.com(查看原文) 阅读量:3 收藏



Too Long; Didn't Read
The approximation to Ξ14 is established through a series of lemmas, propositions, and Cauchy's inequality, integrating results and proofs from various sections.


Author:
(1) Yitang Zhang.
Table of Links
- Abstract & Introduction
- Notation and outline of the proof
- The set Ψ1
- Zeros of L(s, ψ)L(s, χψ) in Ω
- Some analytic lemmas
- Approximate formula for L(s, ψ)
- Mean value formula I
- Evaluation of Ξ11
- Evaluation of Ξ12
- Proof of Proposition 2.4
- Proof of Proposition 2.6
- Evaluation of Ξ15
- Approximation to Ξ14
- Mean value formula II
- Evaluation of Φ1
- Evaluation of Φ2
- Evaluation of Φ3
- Proof of Proposition 2.5
Appendix A. Some Euler products
Appendix B. Some arithmetic sums
13. Approximation to Ξ14
In this section we establish an approximation to Ξ14.
Assume that ψ ∈ Ψ1 and ρ ∈ Z(ψ). By Lemma 5.2 and (2.2),

By Lemma 6.1,

and, by Lemma 5.1,

Hence

By Lemma 6.1 and 5.1,

We insert this into (13.2) and then insert the result into (13.1). Thus we obtain

where


where

Inserting this into (12.4) we obtain

Combining (2.34), Cauchy’s inequality, Proposition 7.1, Lemma 5.9, 6.1 and 3.3, we can verify that

For example, by (2.34)

the right side being estimated via Lemma 5.9, 6.1 and 3.3
文章来源: https://hackernoon.com/discrete-mean-estimates-and-the-landau-siegel-zero-approximation-to-314?source=rss
如有侵权请联系:admin#unsafe.sh
如有侵权请联系:admin#unsafe.sh