【熵密杯】CTF之RSA解密

【熵密杯】CTF之RSA解密
2023-7-30 04:28:25 Author: 利刃信安攻防实验室(查看原文) 阅读量:39 收藏

CTF之RSA解密

小明得到了一个RSA加密信息，你能帮他解开吗？

c=27990707239527629138352696377606718299992092729307910015562504696905353450041
n=41069065654959614597750207738698085798765257876378561837894254544512565197793
e=11

直接分解模数Ｎ

直接分解模数N是最直接的攻击方法，也是最困难的方法。具体的解析同上RSA安全性分析。

如果n小于256bit，可以使用本地工具进行暴力分解，例如Windows平台的RSATool，可以在数分钟之内完成256bit的n的分解。

如果n大于768bit，可以尝试利用在线网站

http://factordb.com/

，这一类在线网站的原理是储存了部分n分解成功的的值。

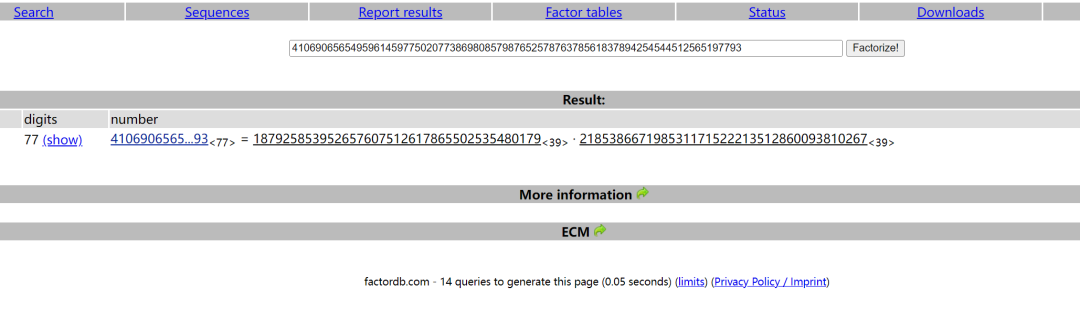
首先对n分解

http://factordb.com/index.php?query=41069065654959614597750207738698085798765257876378561837894254544512565197793

第一个整数P39：187925853952657607512617865502535480179

第二个整数P39：218538667198531171522213512860093810267

分解Ｎ可以通过在线网站

http://www.factordb.com/index.php

分解n可以得到p和q的值为218538667198531171522213512860093810267和187925853952657607512617865502535480179，现在已知p、q、e以及c，可以通过前三个参数求出d

mac安装gmpy2可以参考

https://www.cnblogs.com/c-x-a/p/11810194.html

#!/usr/bin/env python3# -*- coding: utf-8 -*-
import gmpy2from concurrent.futures import ThreadPoolExecutor
def rsa_private_key(p, q, e):    phi_n = (p - 1) * (q - 1)    d = gmpy2.invert(e, phi_n)    return d
if __name__ == "__main__":    # 输入p、q和e    p = gmpy2.mpz(input("请输入第一个整数P39："))    q = gmpy2.mpz(input("请输入第二个整数P39："))    e = gmpy2.mpz(input("请输入公钥e："))
    # 使用多线程处理计算私钥d    with ThreadPoolExecutor() as executor:        future = executor.submit(rsa_private_key, p, q, e)        d = future.result()
    print("模数n分解结果:")    print(f"第一个整数P39为: {p}")    print(f"第二个整数P39为: {q}")    print(f"公钥e为: {e}")    print(f"私钥d为: {d}")

d为14934205692712587126454620995890213017585015765537226566857972060418158511763

到目前为止，已经求出p,q,e,d,n,c，然后可以求出相应的明文M

#求明文

#!/usr/bin/env python3# -*- coding: utf-8 -*-
import gmpy2from concurrent.futures import ThreadPoolExecutor
def rsa_decrypt(ciphertext, n, d):    return pow(ciphertext, d, n)
if __name__ == "__main__":    n = gmpy2.mpz(input("请输入RSA的模数n："))    d = gmpy2.mpz(input("请输入RSA的私钥d："))
    c = input("请输入RSA的密文c，用空格分隔每个块：")    c_list = list(map(gmpy2.mpz, c.split()))
    # 使用多线程处理密文解密    with ThreadPoolExecutor() as executor:        future_to_result = {executor.submit(rsa_decrypt, ciphertext, n, d): ciphertext for ciphertext in c_list}        decrypted_values = [future.result() for future in future_to_result]
    # Convert decrypted integers to bytes and then decode using UTF-8    result = "".join([bytes.fromhex(decrypted_value.digits(16)).decode('utf-8', 'ignore') for decrypted_value in decrypted_values])
    print("解密后的明文为:")    print(result)

#!/usr/bin/env python3# -*- coding: utf-8 -*-
import gmpy2from binascii import a2b_hex
c = hex(27990707239527629138352696377606718299992092729307910015562504696905353450041)n = hex(41069065654959614597750207738698085798765257876378561837894254544512565197793)e = hex(11)p = 218538667198531171522213512860093810267q = 187925853952657607512617865502535480179d = hex(14934205692712587126454620995890213017585015765537226566857972060418158511763)
flag = a2b_hex(hex(pow(c,d,n))[2:])print(flag)

#!/usr/bin/env python3# -*- coding: utf-8 -*-
from binascii import a2b_hex
e = 11d = 14934205692712587126454620995890213017585015765537226566857972060418158511763c = 27990707239527629138352696377606718299992092729307910015562504696905353450041n = 41069065654959614597750207738698085798765257876378561837894254544512565197793
#flag = hex(pow(c,d,n))[1:].decoding("hex")#flag = a2b_hex(hex(pow(c,d,n))[2:])flag = pow(c,d,n)print(flag)

#!/usr/bin/env python3# -*- coding: utf-8 -*-
import gmpy2p = 9648423029010515676590551740010426534945737639235739800643989352039852507298491399561035009163427050370107570733633350911691280297777160200625281665378483q = 11874843837980297032092405848653656852760910154543380907650040190704283358909208578251063047732443992230647903887510065547947313543299303261986053486569407e =  65537c = 83208298995174604174773590298203639360540024871256126892889661345742403314929861939100492666605647316646576486526217457006376842280869728581726746401583705899941768214138742259689334840735633553053887641847651173776251820293087212885670180367406807406765923638973161375817392737747832762751690104423869019034
# 1.已知的p和q求出nn = p * q
# 2.根据已知的条件求出dphi_n = (p-1)*(q-1)d = gmpy2.invert(e,phi_n)#print(d)
#求出明文m = pow(c,d,n)print("m=\n%s"%m)

阅读 10万+

文章来源: http://mp.weixin.qq.com/s?__biz=MzU1Mjk3MDY1OA==&mid=2247505698&idx=4&sn=269fc3a901afec31cc92456a5e6487af&chksm=fbfb67efcc8ceef90398337c416197946664b1a9ce179b719cdcf05baef20ca6a1e41a9ce99d&scene=0&xtrack=1#rd
如有侵权请联系:admin#unsafe.sh