团队科研成果分享

2023.02.06-2023.02.12

01

研究背景

海洋探索是人类社会可持续发展的根本性问题之一，也是实现智慧海洋城市等水下物联网（IoUT）应用概念的基础。基于水下无线通信的异构自主海洋车辆（AMV）之间的协作是一种可行的海洋探测方法，典型的AMV包括自主水面航行器（ASV）和自主水下滑翔机（AUG）。然而，它们的规格和运动的差异给协同工作带来了以下问题：首先，当AUG浮到一定深度与ASV通过水下无线通信进行交互时，这种交互有一定的时间限制，它们运动到交互位置必须同步;其次，在多个AUGs同时进行水下探测的情况下，ASV需要规划水面交互的顺序，以保证及时、高效地数据采集。本文所要解决的问题场景如图1所示。为此，提出了一种面向异构AMVs数据收集的启发式表面路径规划方法（HSPP-HA），为ASV规划一条低路径成本、高数据收集的访问路径，解决了交互点具有时效性的问题。

图1 ASV和多个AUG之间的协作示例

02

关键技术

HSPP-HA通过改进的混合蛙跳算法（SFLA）优化ASV与多个AUG之间的交互调度。该算法采用时空k-means聚类方法初始化SFLA的初始族群，通过加权其时空接近度来适应时间敏感的交互作用；并采用随算法迭代次数变化的自适应收敛因子来平衡局部搜索和全局搜索，使每次局部搜索中潜在的局部最优问题最小化。

该方法的创新和贡献如下：

1）提出了一种基于异构AMVs的水下数据采集水面路径规划方法HSPP-HA。该方法针对水面ASV与水下多个AUGs基于水下无线通信协同采集水下数据的应用场景，针对ASV与AUG之间的时间敏感交互，采用改进的SFLA算法对两者之间的数据采集进行调度。

2）利用时空k-means算法和自适应迭代方法设计了一种改进的SFLA算法。时空k-means算法通过交互点的坐标和出现时间对交互点进行聚类，以初始化局部搜索；同时，自适应迭代因子使得在优化交互序列时能够平衡局部和全局搜索，并且进一步提高收敛能力，提高最终解质量。

03

算法介绍

1. 系统模型

A．任务模型

图2 任务模型

如图2所示，水下多AUGs按照预定的勘探路径运动，会在每个周期形成时间不同的交互点，每个交互点旁边的数字标号表示出现时间的序列。故本文的主要任务便是，ASV以最低的路径成本去访问最多的交互点，收集最多的海洋数据信息。

B．约束模型

交互点具有时间、位置和信息量三个因素。因此，HSPP-HA的路径规划考虑如下三个约束：

时间约束：每个交互点发生在不同的时间，应当被给予不同的优先级。每个交互点的发生时间被表示为时间量，表示为：

其中，N表示任务中交互点的总个数；根据上式可以知道t_1>t_2>…>t_N。t_i越大，ASV越需要优先去访问它。

位置约束（速度约束）：为了确保ASV能够在交互点消失之前到达其位置，ASV应当具有足够的速度以在特定时间段内在相互交互点i和j之间航行，具体表示为：

其中，T_i表示第i个交互点的出现时间；d_{ij}表示交互点i和j之间的欧式距离。

信息负载约束：每个交互点提供不同量的数据，因为一些AUG可能无法在交互作用周期内与ASV完成交互，因此将数据缓冲到下一个交互作用点。然而，缓存应当被限制以确保缓存器中的数据可以在下一个交互周期内被交互，具体表示为：

其中q_i是AUG i采集的数据计数，当AUG i完成一次交互时，复位为0;D是一个交互周期收集的数据量;B为AUG到ASV的无线信道带宽;I_i是i的相互作用周期。

C. 目标优化模型

本文的目标优化模型主要权衡了交互点的时间和位置（本文记述为访问收益N_i），另外，交互点的信息量被用来控制访问的优先级。具体表达如下：

其中μ_i=1-1/(2^(q_i))；ω_1+ω_2=1。其中N_i表达如下：

其中，d_{a→b}是a和b之间的距离;Q是围绕i并遵循位置（速度）约束的交互点的集合;j是Q中的每个交互作用点;n是Q中交互作用点的数目。下面的图3示出了ASV决定要访问的交互点的示例情况，其详细描述了Ni的含义。

图3 访问收益N_i的示例图

在图3中，离ASV最近的交互作用点是6，离交互作用点6最近的交互作用点是8。故ASV访问交互点7的访问收益N_7为：

最后，目标优化函数f_i将作为HSPP-HA算法的评价指标，其值越小，表示解越优。

2. HSPP-HA算法

A．时空聚类

混合蛙跳算法（SFLA）的全局搜索过程在整个区域上搜索族群（子区域），而局部搜索过程在每个族群内搜索优化的解决方案。因此，HSPP-HA首先对交互点进行聚类以形成多个族群，又由于交互点是时间敏感的，所以聚类必须考虑它们的空间和时间接近性，以将具有相似位置和发生时间的交互点分组，用于高效的局部搜索。基于此，本文提出的时空聚类算法利用k-means算法的基本原理，通过对时空接近度进行加权来形成搜索族群。具体细节如下：

假设在{x，y}区域中有N个交互点，交互点记为X = {X_1,X_2,…,X_N}，其中每个交互点i具有二维坐标和其发生时间。由于上述的时间约束模型，交互点发生时间被表示为时间量t_i，且每个交互点（x_i，y_i）的坐标被归一化为（x_i/x，y_i/y），因此，每个交互点i表示为X_i =（x_i/x，y_i/y，t_i）。

根据k-means聚类的原理，本文将初始聚类表示为M = {M^1,M^2,…,M^k},且聚类中心表示为R，然后将交互点i到聚类中心j的时间接近度表示为：

其中P^T是时间接近度。然后，它们之间的空间接近度表示为：

其中P^S是空间接近度；v_{i→j}是ASV从i航行到j所需的速度，该速度可以通过它们出现的时间和位置的差来计算；C^v_{i→j}是上述的速度约束。

最后，联合接近度表示为：

式中P为联合接近度；η_1、η_2是通过求解下面的等式计算得到的加权值：

其中P^T_{AVG_M^j}、P^S_{AVG_M^j}分别是M^j中平均的时间和空间接近度，P^T_{MAX_M^j}、P^S_{MAX_M^j}分别是M^j中的最大时间和空间接近度。时空聚类算法的输出将作为SFLA的搜索族群。

B．自适应迭代的混合蛙跳算法

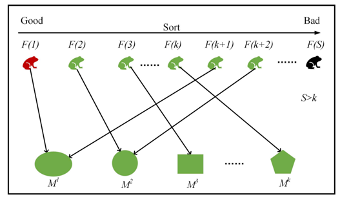
在本文的任务模型中，一只青蛙的行为代表了一个路径解，它是一条访问交互点的路径序列，它的跳跃向量是两个交互点之间的路径。青蛙的种群表示为{F（1）,F（2）,…,F（S）}，每个F（i）都有一个路径适应度值f（i）（见公式（4））。种群青蛙按升序排序，具有最佳适应度值的青蛙是F（1），表示为P_G。然后，通过以下方式将排好序的青蛙分配到族群M^j：

其中k是族群的数目；j是族群的序列；i是青蛙群体的序列。图4给出了青蛙种群分配示意图。

图4 青蛙种群分配示例图

接下来，M^j中的每个青蛙执行局部搜索过程，该过程包含三种类型的跳跃更新机制（LUM）。局部搜索过程在全局搜索过程的每一轮期间执行，其中针对每个M^j执行局部搜索以确定局部最优解并更新或淘汰最差解。

然后，根据概率p_i = 2(n+1−i)/n(n+1)从M^j中选出q（q<n）只青蛙，形成子族群SM^j，用于局部搜索。青蛙的f（i）越小，被选入到SM^j的概率越高。该选择过程是随机的，以确保所选择的q只青蛙完全反映该族群M^j的青蛙信息。在SM^j中，最好的青蛙被表示为P_B，最差的青蛙是F（q），被表示为P_W。图5给出了HSPP-HA的原理示意图。

图5 HSPP-HA的原理图

图5给出了一个全局迭代的例子。在每一次迭代循环中，种群S被更新优化以确定最优青蛙（红青蛙），M^j是包含n只青蛙的区域，在每一次迭代中从n只青蛙中选择q只青蛙以形成SM^j，并且在一次迭代之后SM^j中的青蛙和M^j中的其它青蛙被更新和交换（绿色青蛙）。SM^j中的青蛙被排序以获得局部最优青蛙（蓝色青蛙）、局部最差青蛙（黑色青蛙）和其他青蛙（橙色青蛙）。另外，红色、橙色和蓝色虚线表示P_W的三种类型的LUM，具体内容如下所述：

其中F^'_{i}(q)(i=1,2,3)是最差解P_W在三种类型的LUM下的更新解；R是(0,1)之间的随机数组;λ_i(i=1,2,3)是三种类型的LUM的更新因子;△_i(i=1,2,3）是三种类型的LUM的更新方法;λ_{max}是三种类型的LUM 中的最大更新因子，其控制算法的全局搜索能力。这三种类型的LUM更新方法分别如下：

第一类型的LUM根据SM^j中的P_B更新P_W，更新方法△_1表示为：

在传统的SFLA中，如果P_W在根据P_B更新之后不能被改善，则在可行解空间中随机生成的青蛙替换旧的差青蛙。随机生成是为了从种群中消除最差解，且有利于快速收敛，但是不利于总体种群的进化。因此，为第二类型LUM设了用于在每次迭代中的自适应因子，其表示为：

其中δ为自适应迭代因子，t为当前迭代次数;tmax是最大迭代次数；r是（0，1）之间的随机数。这种方法的思想是，P_W应该向P_B学习，因为它们属于相同的M^j，并且在迭代早期，差青蛙模仿好青蛙的学习行为应该考虑算法的收敛速度和全局搜索能力。在保证不陷入局部最优的同时,δ值越大越好，以加快学习速度，并保证较大的搜索空间;而在迭代后期，应该考虑算法的局部搜索能力以提高解的精确度，因此δ应该是较小的值以减慢学习速度并确保局部搜索能力，这最终平衡了局部和全局搜索。

第三类型的 LUM执行全局搜索。在当前迭代轮数下，用全局最佳青蛙P_G更新P_W，更新方法△3表示为：

通过三种类型的LUM，SM^j中的最差青蛙F(q)被优化更新，并且M^j中的最差青蛙被淘汰。然后，M^j中的青蛙根据f(i)被递增地重新排序以确定新的M^j。当每个M^j的迭代已经达到最大迭代次数并且已经搜索了所有Mj，最终返回由P_G表示的最优路径。

04

实验结果

1. 实验结果

图6示出了由多个AUGs生成的交互点的示例。虚线表示AUG轨迹的俯视图，图中交互点按数字顺序出现，经过一定时间后消失。每个AUG在其浮动到交互点时携带一定量的数据，并且如果ASV错过交互作用，则AUG将把数据缓存到下一交互点。但是本文仿真最多缓存三次，因为在超过三次缓存的情况下，缓存的数据超过一个交互周期的可传输量，这会导致数据丢失。目标是规划ASV在海面上的优化路径，顺序地访问多的交互点同时收集尽可能多的数据。

图6 3个AUGs生成的交互点的示例图

图7 不同交互点数目下的ASV路径长度、访问率、数据收集率图

通过图7可以发现，在路径长度和访问率方面，所提出的HSPP-HA 展示出了预期的最高性能，并且SFLA紧随其后，这证明了时空聚类对本文的任务模型的适应性。H-MOPSO和JS示出较低的性能，因为它们的机制中每个交互点的时间和空间属性不相关，从而混淆路径规划决策。由于采用了自适应迭代方法，所提方法优于SFLA。特别是在数据收集率方面，由于自适应迭代因子很好地平衡了全局和局部搜索，因此与原始SFLA相比，其显示出显著的改进，其中在300个交互作用点的情况下，数据收集率增加了20%以上，在50个交互作用点的情况下，数据收集率达到98%。

为了进一步分析详细的过程，在下面的图8中比较了使用四种算法规划的路径，其中三个AUG在100m×100m 区域中工作，并生成30个交互点。

图8 四种算法下的ASV路径图

在图8中，三条虚线表示3个AUG轨迹的俯视图，实线表示ASV的路径。图8a示出了在H-MOPSO下的路径，其中ASV成功地访问了23个交互作用点，访问率为76.67%。在来自AUG 1的交互作用点13、15、19和20的情况下，ASV无法收集交互点13、15和19上的数据，因为它们不满足信息负载约束，而交互点20的数据可以缓存到25上而被收集。在交互点29的情况下，交互点27到29之间的路径不满足速度约束，即ASV放弃访问交互点29而直接访问交互点30，即交互点29上的数据丢失。此时，数据收集率为86.67%，路径长度为547.8m。图8b示出了JS下的路径，其中ASV 成功地访问了20个交互作用点，访问率为66.67%，并且基于相同的原因，在交互作用点20和25上的数据没有被成功地收集。数据收集率和路径长度分别为93.33%和501.3m，这展示了与H-MOPSO相比改进的性能，尽管具有较低的访问率。

图8c示出了SFLA下的路径，ASV的访问率为70%，数据收集率为93.33%和路径长度为436.8m；图8d示出了所提HSPP-HA下的路径，ASV的访问率为73.33%，数据收集率为100%和路径长度为411.6m。由于采用了时空聚类，根据交互点的出现时间对每条路径进行调度，从而带来了更高的数据采集率。

05

总结

AMV协作是实现物联网应用的基础技术之一。本文提出了一种用于交互的异构AMV的启发式水面路径规划方法，称为HSPP-HA，其被设计用于海面上的ASV访问由水下AUG生成的一系列时间敏感的交互点的应用场景。HSPP-HA基于SFLA，并进行了一些改进，包括时空聚类和自适应迭代因子。时空聚类将在时间和空间上接近的AUG的交互点分配给同一区域以初始化SFLA 的族群，这在调度时间敏感交互方面具有优势;自适应迭代因子调整SFLA在不同迭代阶段的收敛速度，平衡算法的局部搜索和全局搜索，在一定程度上避免局部最优问题。仿真结果表明，与经典方法和最新方法相比，该方法在生成路径长度、时间敏感交互点的访问率、数据收集率等方面具有优势。然而，所提出的算法仍然有一些改进的空间，因为目标优化函数没有考虑ASV的运动约束，这将在我们未来的工作中进行研究，并且我们未来的工作还将集中于设计用于水下AMV的水下路径规划方法，该水下路径规划方法应当考虑复杂的水下地形、不规则的洋流和动态障碍物等。

扫描二维码关注我们