
1 引言
之前介绍了Redis的数据存储及String类型的实现,接下来再来看下List、Hash、Set及Sorted Set的数据结构的实现。
2 List
List类型通常被用作异步消息队列、文章列表查询等;存储有序可重复数据或做为简单的消息推送机制时,可以使用Redis的List类型。对于这些数据的存储通常会使用链表或者数组作为存储结构。
使用数组存储,随机访问节点通过索引定位时间复杂度为O(1)。但在初始化时需要分配连续的内存空间;在增加数据时,如果超过当前分配空间,需要将数据整体搬迁移到新数组中。
使用链表存储,在进行前序遍历或后续遍历,当前节点中要存储前指针和后指针,这两个指针在分别需要8byte共16byte空间存储,存在大量节点会因指针占用过多空间。链表虽然不需要连续空间存储可以提高内存利用率,但频繁的增加和删除操作会使内存碎片化,影响数据读写速率。
如果我们能够将链表和数组的特点结合起来就能够很好处理List类型的数据存储。
2.1 ZipList
3.2之前Redis使用的是ZipList,具体结构如下:
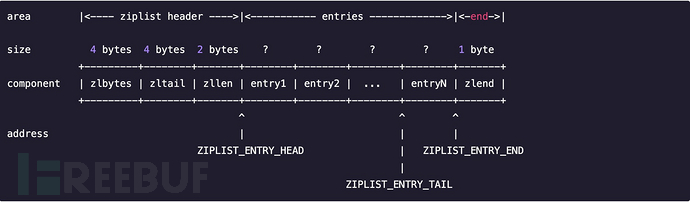
zlbytes: 4byte 记录整个压缩列表占用的内存字节数:在对压缩列表进行内存重分配, 或者计算 zlend 的位置时使用。
zltail:4byte 记录压缩列表表尾节点距离压缩列表的起始地址有多少字节: 通过这个偏移量,程序无须遍历整个压缩列表就可以确定表尾节点的地址。
zllen:2byte 记录了压缩列表包含的节点数量: 当这个属性的值小于 UINT16_MAX(65535)时, 这个属性的值就是压缩列表包含节点的数量; 当这个值等于UINT16_MAX 时,节点的真实数量需要遍历整个压缩列表才能计算得出。
entry X:压缩列表包含的各个节点,节点的长度由节点保存的内容决定。包含属性如下:
prerawlen:记录前一个节点所占内存的字节数,方便查找上一个元素地址
len:data根据len的首个byte选用不同的数据类型来存储data
data:本元素的信息
zlend: 尾节点 恒等于255
ziplist是一个连续的内存块,由表头、若干个entry节点和压缩列表尾部标识符zlend组成,通过一系列编码规则,提高内存的利用率,使用于存储整数和短字符串。每次增加和删除数据时,所有数据都在同一个ziplist中都会进行搬移操作。如果将一个组数据按阈值进行拆分出多个数据,就能保证每次只操作某一个ziplist。3.2之后使用的quicklist与ziplist。
2.2 QuickList
quicklist就是维护了一种宏观上的双端链表(类似于B树),链表的节点为对ziplist包装的quicklistNode,每个quciklistNode都会通过前后指针相互指向,quicklist包含头、尾quicklistNode的指针。
typedef struct quicklist {
quicklistNode *head;
quicklistNode *tail;
unsigned long count; /* total count of all entries in all ziplists */
unsigned long len; /* number of quicklistNodes */
int fill : QL_FILL_BITS; /* fill factor for individual nodes */
unsigned int compress : QL_COMP_BITS; /* depth of end nodes not to compress;0=off */
...
} quicklist;
*head:表头节点
*tail:表尾节点
count:节点包含entries数量
len:quicklistNode节点计数器
fill:保存ziplist的大小,配置文件设定
compress:保存压缩程度值,配置文件设定
quicklistNode:
typedef struct quicklistNode {
struct quicklistNode *prev;
struct quicklistNode *next;
unsigned char *zl;
unsigned int sz; /* ziplist size in bytes */
unsigned int count : 16; /* count of items in ziplist */
。。。
} quicklistNode;
*prev:前置节点
*next:后置节点
*zl:不进行压缩时指向一个ziplist结构,压缩时指向quicklistLZF结构(具体内容请参考下方链接)
sz:ziplist个数
count:ziplist中包含的节点数
在redis.conf通过设置每个ziplist的最大容量,quicklist的数据压缩范围,提升数据存取效率,单个ziplist节点最大能存储量,超过则进行分裂,将数据存储在新的ziplist节点中
-5: max size: 64 Kb <— not recommended for normal workloads
-4: max size: 32 Kb <— not recommended
-3: max size: 16 Kb <— probably not recommended
-2: max size: 8 Kb <— good
-1: max size: 4 Kb <— good
List-max-ziplist-size -2
0代表所有节点,都不进行压缩,1.代表从头节点往后一个,尾结点往前一个不用压缩,其它值以此类推
List-compress-depth 1
Redis 的链表实现的特性可以总结如下:
双端:链表节点带有prev和next指针, 获取某个节点的前置节点和后置节点的复杂度都是O(1) 。
无环:表头节点的prev指针和表尾节点的next指针都指向NULL,对链表的访问以NULL为终点。
带表头指针和表尾指针:通过list结构的head指针和tail指针,程序获取链表的表头节点和表尾节点的复杂度为O(1) 。
带链表长度计数器:程序使用list结构的len属性来对list持有的链表节点进行计数,程序获取链表中节点数量的复杂度为O(1)。
3 Hash
存储一个对象,可以直接将该对象进行序列化后使用String类型存储,再通过反序列化获取对象。对于只需要获取对象的某个属性的场景,可以将将每个属性分别存储;但这样在Redis的dict中就会存在大量的key,对于键时效后的回收效率存在很大影响。使用Map结构就可以再dict的存储中只存在一个key并将属性与值再做关联。
Redis的Hash数据结构也是使用的dict(具体实现可以查看上一篇,浅谈Redis数据结构(上)-Redis数据存储及String类型的实现)实现。当数据量比较小,或者单个元素比较小时,底层使用ziplist存储,数据量大小和元素数量有如下配置:

ziplist元素个数超过512,将改为hashtable编码
hash-max-ziplist-entries 512
单个元素大小超过64byte时,将改为hashtable编码
hash-max-ziplist-value 64

4 Set
Set类型可以在对不重复集合操作时使用,可以判断元素是否存在于集合中。Set数据结构底层实现为value为null的dict,当数据可以使用整形表示时,Set集合将被编码为intset结构。
typedef struct intset {
uint32_t encoding;
uint32_t length;
int8_t contents[];
} intset;
整数集合是一个有序的,存储整型数据的结构。整型集合在Redis中可以保存xxxx的整型数据,并且可以保证集合中不会出现重复数据。

使用intset可以节省空间,会根据最大元素范围确定所有元素类型;元素有序存储在判断某个元素是否存在时可以基于二分查找。但在以下任意条件不满足时将会使用hashtable存储数据。
元素个数大于配置的set-max-inset-entries值
元素无法用整型表示

5 Sorted Set
连续空间存储数据,每次增加数据都会对全量数据进行搬运。对于有序链表查找指定元素,只能通过头、尾节点遍历方式进行查找,如果将每个数据增加不定层数的索引,索引之间相互关联,寻找指定或范围的元素时就可以通过遍历层级的索引来确定元素所处范围,减少空间复杂度。跳跃表是一种可以对有序链表进行近似二分查找的数据结构,redis 在两个地方用到了跳跃表,一个是实现有序集合,另一个是在集群节点中用作内部数据结构。
跳跃表 ( skiplist ) 是一种有序数据结构,自动去重的集合数据类型,ZSet数据结构底层实现为字典(dict) + 跳表(skiplist)。它通过在每个节点中维持多个指向其他节点的指针,从而达到快速访问节点的目的。支持平均O ( logN ) 、最坏 O(N) 复杂度的节点查找,还可以通过顺序性操作来批量处理节点。
数据比较少时,用ziplist编码结构存储,包含的元素数量比较多,又或者有序集合中元素的成员(member) 是比较长的字符串时,Redis 就会使用跳跃表来作为有序集合键的底层实现。
元素个数超过128,将用skiplist编码
zset-max-ziplist-entries 128
单个元素大小超过64 byte,将用skiplist编码
zset-max-ziplist-value 64
5.1 跳跃表
zset结构如下:
typedef struct zset {
// 字典,存储数据元素
dict *dict;
// 跳跃表,实现范围查找
zskiplist *zsl;
} zset;
robj *createZsetObject(void) {
// 分配空间
zset *zs = zmalloc(sizeof(*zs));
robj *o;
// dict用来查询数据到分数的对应关系,zscore可以直接根据元素拿到分值
zs->dict = dictCreate(&zsetDictType,NULL);
// 创建skiplist
zs->zsl = zslCreate();
o = createObject(OBJ_ZSET,zs);
o->encoding = OBJ_ENCODING_SKIPLIST;
return o;
zskiplist
typedef struct zskiplist {
// 头、尾节点;头节点不存储元素,拥有最高层高
struct zskiplistNode *header, *tail;
unsigned long length;
// 层级,所有节点中的最高层高
int level;
} zskiplist;
typedef struct zskiplistNode {
// 元素member值
sds ele;
// 分值
double score;
// 后退指针
struct zskiplistNode *backward;
// 节点中用 L1、L2、L3 等字样标记节点的各个层, L1代表第一层, L2代表第二层,以此类推。
struct zskiplistLevel {
// 指向本层下一个节点,尾节点指向null
struct zskiplistNode *forward;
// *forward指向的节点与本节点之间的元素个数,span值越大,跳过的节点个数越多
unsigned long span;
} level[];
} zskiplistNode;
结构图如下:
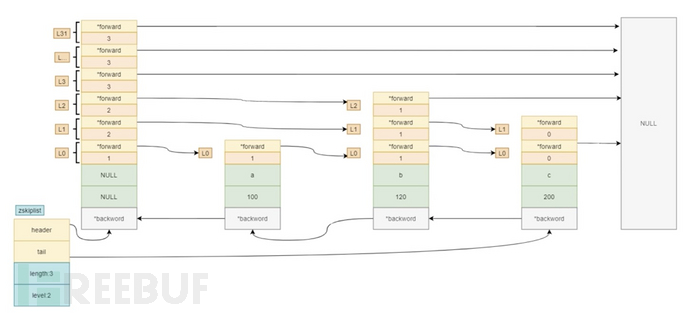
5.2 创建节点及插入流程
SkipList初始化,创建一个有最高层级的空节点:
zskiplist *zslCreate(void) {
int j;
zskiplist *zsl;
// 分配空间
zsl = zmalloc(sizeof(*zsl));
// 设置起始层次
zsl->level = 1;
// 元素个数
zsl->length = 0;
// 初始化表头,表头不存储元素,拥有最高的层级
zsl->header = zslCreateNode(ZSKIPLIST_MAXLEVEL,0,NULL);
// 初始化层高
for (j = 0; j < ZSKIPLIST_MAXLEVEL; j++) {
zsl->header->level[j].forward = NULL;
zsl->header->level[j].span = 0;
}
// 设置表头后退指针为NULL
zsl->header->backward = NULL;
// 初始表尾为NULL
zsl->tail = NULL;
return zsl;
}
新增元素:
zskiplistNode *zslInsert(zskiplist *zsl, double score, sds ele) {
zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
unsigned int rank[ZSKIPLIST_MAXLEVEL];
int i, level;
serverAssert(!isnan(score));
x = zsl->header;
// 遍历所有层高,寻找插入点:高位 -> 低位
for (i = zsl->level-1; i >= 0; i--) {
// 存储排位,便于更新
rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];
while (x->level[i].forward &&
// 找到第一个比新分值大的节点,前面一个位置即是插入点
(x->level[i].forward->score < score ||
(x->level[i].forward->score == score &&
// 相同分值则按字典顺序排序
sdscmp(x->level[i].forward->ele,ele) < 0)))
{
// 累加跨度
rank[i] += x->level[i].span;
x = x->level[i].forward;
}
// 每一层的拐点
update[i] = x;
}
// 随机生成层高,以25%的概率决定是否出现下一层,越高的层出现概率越低
level = zslRandomLevel();
// 随机层高大于当前的最大层高,则初始化新的层高
if (level > zsl->level) {
for (i = zsl->level; i < level; i++) {
rank[i] = 0;
update[i] = zsl->header;
update[i]->level[i].span = zsl->length;
}
zsl->level = level;
}
// 创建新的节点
x = zslCreateNode(level,score,ele);
for (i = 0; i < level; i++) {
// 插入新节点,将新节点的当前层前指针更新为被修改节点的前指针
x->level[i].forward = update[i]->level[i].forward;
update[i]->level[i].forward = x;
// 新节点跨度为后一节点的跨度 - 两个节点之间的跨度
x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);
update[i]->level[i].span = (rank[0] - rank[i]) + 1;
}
// 新节点加入,更新顶层 span
for (i = level; i < zsl->level; i++) {
update[i]->level[i].span++;
}
// 更新后退指针和尾指针
x->backward = (update[0] == zsl->header) ? NULL : update[0];
if (x->level[0].forward)
x->level[0].forward->backward = x;
else
zsl->tail = x;
zsl->length++;
return x
}
如有侵权请联系:admin#unsafe.sh