团队科研成果分享

2022.07.25-2022.07.31

01

研究背景

由于能源和生产需求的急剧增加，海上开采和运输已变得普遍。不幸的是，所有这些活动都极大地危害了海洋生态。例如海上石油泄露、有毒化学品排放和赤潮爆发等。发生此类事件后，必须立即采取精确行动，以减少或控制事件的进一步恶化。最近的研究中将浮油、化学品等理解为一个连续目标，提出连续目标的概念是为了模拟来自一个源并随时间扩散的物质的几何形状。

早期连续目标的边界追踪方法是利用手持设备。但这些方法需要大量的人力和时间，且无法保证实时追踪。最近，无人机（UAV）和图像处理的结合被认为可以通过更高的自动化程度降低所需的最低人工干预程度。然而，许多实际问题仍然存在——例如，恶劣天气事件可能会阻止无人机正常运行。此外，由于连续目标中处于扩散过程，仅使用无人机扫描整个区域非常耗时。水声传感器网络（UASN）的发展为检测和追踪连续目标提供了强大的技术支持。低成本的微传感器节点可以协作同步监测连续目标。由于连续目标可以完全由其边界定义，因此使用边界附近的节点是一种合理的方法。过去的研究利用内部边界节点和外部边界节点，以及由内部和外部节点包围的边界面来进行边界追踪，如图1所示。从图中已看出，这种方法会使外部或内部节点拟合的追踪边界超过或低估实际边界。

图1 基于边界节点或多边形面的连续目标追踪

02

关键技术

本文提出了一种基于连续目标可行域搜索的分布式边界跟踪算法（FRSCO）。为了确定实际边界所在的可行区域，FRSCO首先将连续目标限制在最小椭圆边界内。在最小边界椭圆内，通过二叉树结构进行晶胞划分，从中选择一组骨干晶胞，从而粗略地定位可行域。通过构造和解构每个骨干晶胞中节点的凸包，进一步缩小可行域位置的不确定性。应用最大熵原理，在最终可行域中引入虚拟节点来确定边界节点，最后估计可行域内实际边界的位置。

该方法的创新和贡献如下： 

1）自适应地建立最小边界椭圆来表征由水流引起的连续目标边界的各向异性特性，同时最小化实际边界的最大可行区域。

2）尽可能使用最小边界椭圆中节点的凸包来减少最大可行区域的不确定性。边界跟踪仅在受限可行区域内执行。

3）创建虚拟边界节点以接近实际边界，而不是实际传感器节点。在不高估或低估实际边界的情况下，能够获得合理的追踪结果。

03

算法介绍

由于连续目标以近乎椭圆的轮廓扩散，本文提出传感器网络中覆盖整个连续目标的最小边界椭圆的概念。在最小边界椭圆内，我们基于二叉树结构进行晶胞划分，选择一些骨干晶胞来刻画可行域的粗略轮廓。

1. 各向异性扩散

图2 由 BTS-COT 构建的循环网络

在水环境中，水流的运动导致下垫面不稳定，导致各向异性扩散。如图2（a）所示，由于最小外接圆本质上是各向同性的，无法表征复杂流体动力学模式产生的各向异性边界。图 2(b) 表明，当各向异性边界由规则圆刻画时，可能会导致较大的误差。为了将各向异性行为结合到所提出的算法中，利用最小边界椭圆而不是圆形。

2. 最小边界椭圆的构建 

传感器节点能够感应化学信号以检测连续目标的存在。如果化学信号超过预设阈值，则认为该节点位于连续目标内，将该节点称为事件节点。否则，该节点被认为在连续目标之外并称为正常节点。如图3（a）所示，所有节点都根据所在位置组织成集群，包含事件节点的集群称为事件集群。

当事件节点检测到连续目标时，事件节点将其ID和位置信息发送给簇头CHi。根据接收到的信息，CHi 先生成一个局部四元组来刻画簇i中目标所覆盖的区域，如图 3(b) 所示。然后再将全局四元组中的事件节点以顺时针方式连接起来，组成一个多边形Q。此外，引入四个集合S1、S2、S3和S4，分别存储Q之外最近边为 A1B4、B4C3、C3C2和C2A1 的事件节点。集合S1、S2、S3和S4中的节点将通过快速凸包算法选择作为Q的新增顶点。如图3（c）所示，事件节点所在的区域可以被更新后的Q完全覆盖。

最后根据旋转卡壳算法，旋转四条支撑线，使一条（或两条）线与Q的边缘重合，如图3（d）所示。由四条线确定几个矩形，直到完全扫描Q，面积最小的矩形是Q的最小外接矩形。

图3 最小边界椭圆的构建

3. 基于二叉树结构的晶胞划分和骨干晶胞选取

将上一步得到的最小包围椭圆均匀地划分为H个环形区域。如图 4 所示，椭圆被划分为6个环形区域，进一步划分每个环形区域后，得到编号为1-63的63个晶胞。位于最外层的单位晶胞称为叶子晶胞，每个晶胞都可以看作一个父晶胞，左右有两个子晶胞。

图4 基于二叉树结构的晶胞划分

根据晶胞中事件节点的分布情况，选择满足以下条件之一的晶胞作为骨干晶胞：

1) 包含事件节点的叶子晶胞（例如图3中的晶胞5、36、47和48）; 

2) 晶胞包含事件节点，并且其叶子晶胞中至少有一个不包含任何事件节点（例如图4中的晶胞9、12、13和14）。

当所有的骨干晶胞都被识别出来后，就可以得到可行区域的粗略轮廓。

4. 边界检测

在骨干晶胞集合所占据的区域内，我们通过构建和解构骨干晶胞中节点的凸包来进一步缩小可行区域。根据节点的类型，凸包可分为以下三种类型，包括骨干晶胞中节点集P的凸包Conv(P)，骨干晶胞中事件节点集E的凸包Conv(E)，骨干晶胞中正常节点集N的凸包Conv(N)。

默认情况下，集合中的节点是非共线的。Eline表示E中的节点共线，Nline 表示N中的节点共线，|·|表示集合中节点的基数。根据每个骨干晶胞中节点的数量和类型，可以通过以下七种情况进一步限制可行域。

图5 可行域限定

Case 1  |E|≥3 && |N|≥3

在这种情况下，分别构造Conv(P)、Conv(E)和Conv(N)，集合INTS来存储 Conv(E)和Conv(N)相交的边。如果|INTS|=0，表示Conv(E)和Conv(N)不相交。如图5（a）所示，由事件节点构建事件凸包A，非事件节点构建非事件凸包B。凸包C为全局凸包，包含事件凸包A和非事件凸包B，可行域可确定为C-(A∪B)。

如果|INTS|≠0，选择INTS中最长的一条边ij进行重构。在图5（b）中，凸包A和B相交，并INTS 中的最长边是mn。存在节点p使得∠mpn最大，因此边mn可重构为边mp和边np。由于两个多边形仍然相交，继续选择节点q最大化∠mqp，并将mp重构为mq和pq，最终的可行区域是C-(G∪F)。如图 5(c)所示，A和B相交，并且A中没有节点到重构多边形，INTS中最长边uv属于多边形A，所以可行域为C-B。

Case 2 |Eline|>0 && |Nline|>0 && |P|≥3

在这种情况下，仅构造Conv(P)，可行域为Conv(P)。在图5（d）中，事件节点和非事件节点各自共线，难以各自进行凸包的构造，此时全局凸包C即为可行域。

Case 3 0<|E|<3 && 0<|N|<3 && |P|≥3

如图5（e）所示，事件节点和非事件节点的数量均小于3，此时可行域为全局凸包C。

Case 4 |E|≥3 && |Nline|>0

在这种情况下，可构造Conv(P)和Conv(E)，则可行域为Conv(P)- Conv(E)。在图5（f）中，凸包A为事件凸包，可行域为C−A。

Case 5 |N|≥3 && |Eline|>0

在这种情况下，可构造Conv(P)和Conv(NE)，则可行域为Conv(P)- Conv(N)。在图5（g）中，凸包B为非事件凸包，可行域为C−B。

Case 6 |E|≠0 && |N|=0

Case 6可分为两个子例。若骨干晶胞不为叶子晶胞，则骨干晶胞的节点与其孩子晶胞中的节点协作构造Conv(P)、Conv(E)和Conv(NE)，并基于Case 1-5进行可行域限定。如图5（h）所示，根据Case 1，可行域表示为C−(A∪B)。若骨干晶胞为叶子晶胞，在图 5(i) 中，晶胞i是具有所有事件节点的骨干晶胞。晶胞i中的节点以及晶胞i-1和晶胞i+1中的节点分别根据Case 4 进行可行域限定。

Case 7 |E|≠0 && |Pline|>0

Case 7也进一步分为两个子例。若骨干晶胞不为叶子晶胞，则骨干晶胞的节点与其孩子晶胞中的节点进行联合构造Conv(P)、Conv(E)和Conv(N)，并基于Case 1-5进行可行域的限定。以图5（j）为例，根据 Case 5可行域表示为C−B。若骨干晶胞为叶子晶胞，骨干晶胞的节点与其兄弟晶胞中的节点进行联合构造Conv(P)、Conv(E)和Conv(N)，并基于Case 1-5进行可行域的限定，根据Case 5可确定可行域。

5. 基于信息熵的边界节点确定

信息熵的概念用来表达连续目标可能出现在某个区域的确定性，通过分配边界节点来最大化该区域的信息熵。本文考虑了事件节点和正常节点，熵函数H可表示为

其中p表示事件节点的比例，q = 1-p表示正常节点。

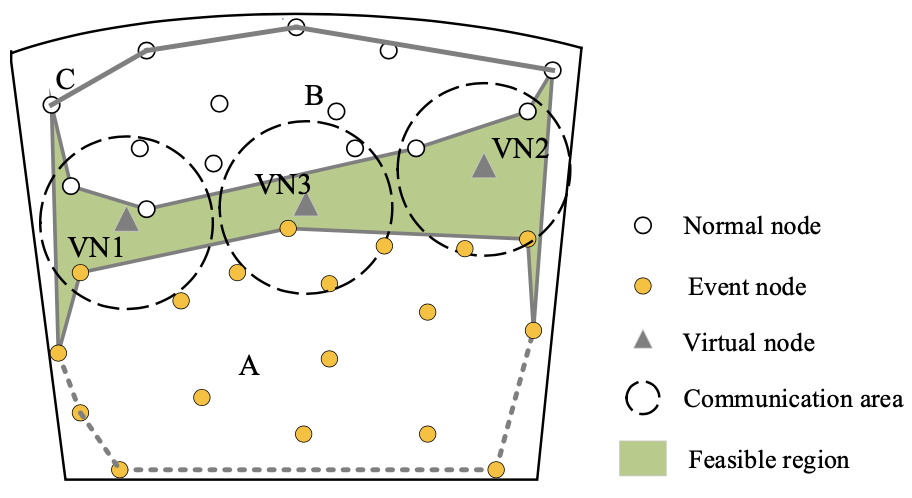
在可行域中引入虚拟节点来确定边界节点的数量和位置。部署虚拟节点，直到虚拟节点在可行域内的通信范围覆盖率达到预设阈值Cth。如图6所示，VN1、VN2和VN3为3个虚拟节点。部署虚拟节点后，可计算在每个虚拟节点通信范围内的可行域内要分配的边界节点数（Nb）。

其中T是虚拟节点通信范围内的节点数。

若Nb = 0，则虚拟节点将被视为边界节点，若 ，则以虚拟节点为中心，以虚拟节点到网络中心的方向及其垂直方向为基准，将通信范围划分为等面积的四个扇区，在每个扇区的可行区域中随机分配一个候选边界节点。

图6 虚拟节点部署

04

实验结果

1. 物理实验测试

FRSCO 首先通过在水池中进行实际测试台实验来验证，如图7(a) 所示。们设计了TDS传感器节点来跟踪罗丹明B的扩散，如图7(b) 所示。在水池中部署了一个由24个节点组成的传感器网络，网络的拓扑结构如图8(a) 所示。最终的边界追踪结果如图8(b)所示，红色曲线代表 OpenCV 提供的实际边界，而蓝色曲线代表 FRSCO 拟合的跟踪边界，连续目标实际边界内的红点是事件节点，而边界外的蓝点是正常节点。FRSCO创建的边界节点用绿色三角形表示。

图7 物理试验台设置

图8 FRSCO 在测试台实验中的边界跟踪结果

2. 仿真实验

仿真实验在MATLAB中实现。如图9所示，可以观察到，根据连续目标的扩散情况，最小椭圆形包络是自适应和可重构的。在扩散过程中，全局四元组中的事件节点被更新。实验结果表明，FRSCO很好地表征了连续目标的扩散。图10显示了椭圆的大小和FRSCO产生的通信开销。

图9 FRSCO算法边界跟踪快照

图10 能量消耗和椭圆面积与扩散时间的关系

3. FRSCO参数测试

   FRSCO将最小包围椭圆的层数、覆盖阈值和节点数作为输入，评估不同参数对算法性能的影响。仿真参数的值列于表1，评价指标包括边界节点数、重叠率、轮廓精度。重叠率的数学定义为：

其中Sest表示的是算法拟合边界所围成区域的面积， Sact表示的是连续目标的实际覆盖面积。

轮廓精度可以定义为

表1 仿真参数设置

图11显示了FRSCO在不同网络规模下的性能。可以得出，当节点数大于50时，FRSCO的性能随着节点数的增加而提高。图12描述了最小边界椭圆的层数与边界节点数之间的关系。可以看出，随着最小包围椭圆层数的增加，边界节点的数量总体呈上升趋势。

图11 重叠率和轮廓精度与节点数的关系

图12 边界节点数与最小边界椭圆层数的关系

图13描绘了最小边界椭圆的层数、重叠率和轮廓精度之间的关系。可以看出，重叠率和轮廓精度都随着最小包围椭圆层数的增加而增加。当最小包围椭圆的层数达到6层时，重叠率和轮廓精度开始收敛。

图13 重叠率和轮廓精度与最小边界椭圆的层数的关系

05

总结

本文研究了基于水声传感器网络的连续目标边界跟踪问题，提出了一种基于可行区域搜索的分布式连续目标边界跟踪算法（FRSCO），将连续目标的扩展范围由最小边界椭圆划定，并基于二叉树结构进行晶胞划分，以使用一组骨干晶胞定位可行域。为了进一步缩小可行域并减少不确定性，所提出的方法在每个骨干晶胞中构造和解构节点的凸包。在最终可行域中引入虚拟节点，利用最大熵原理创建边界节点。通过与基线算法对比研究的实验结果表明，该方法实现了较高的边界跟踪精度。

扫描二维码关注我们