2021-11-19 09:00:00 Author: arthurchiao.github.io(查看原文) 阅读量:128 收藏
Published at 2021-11-19 | Last Update 2021-11-19
译者序
本文翻译自 1974 年关于可虚拟化计算机架构(即能支持 VM)的经典 论文:
Popek, Gerald J., and Robert P. Goldberg. "Formal requirements for virtualizable third generation architectures." Communications of the ACM 17.7 (1974): 412-421.
虽然距今已半个世纪,但这篇文章的一些核心思想仍未过时。特别是,它在最朴素的层面 介绍了虚拟机是如何工作的(就像 (译) RFC 1180:朴素 TCP/IP 教程(1991) 在最朴素的层面介绍 TCP/IP 是如何工作的一样,虽然本文更晦涩一些),这些内容对理解虚拟化的底层原理有很大帮助。
第 1~4 代计算机架构的介绍可参考 Evolution of Computers from First Generation to Fourth Generation:
- 第一代:1940 – 1958
- 第二代:1958 – 1964
-
第三代:1964 ~ 1974,特点:
- 使用集成电路取代晶体管
- High-level 编程语言
- 磁质存储
- 第四代:1974 ~ 今
由于译者水平有限,本文不免存在遗漏或错误之处。如有疑问,请查阅原文。
以下是译文。
- 译者序
- 1. 虚拟机概念(Virtual Machine Concepts)
- 2. 一种第三代计算机模型(A Model of Third Generation Machines)
- 3. 指令行为(Instruction Behavior)
- 4. Virtual Machine Monitor (VMM)
- 5. 虚拟机的特性(Virtual Machine Properties)
- 6. 关于主定理的讨论(Discussion of Theorem)
- 7. 递归虚拟化(Recursive Virtualization)
- 8. 混合虚拟机(Hybrid Virtual Machines)
- 9. 总结
- 附录
- References
少数几种第三代计算机系统 —— 例如 IBM 360/67 的 CP-67 —— 已经实现了虚拟机系统 (virtual machine systems)。 而经验研究指出:某些第三代计算机系统,例如 DEC PDP-10,是无法支持虚拟机系统的。
本文将提出一种泛第三代(third-generation-like)计算机系统,并用一些 规范化技术(formal techniques)来推导出这种架构支持虚拟机的充分条件。
关键字/词: operating system, third generation architecture, sensitive instruction, formal requirements, abstract model, proof, virtual machine, virtual memory, hypervisor, virtual machine monitor
1.1 虚拟机(VM)和虚拟机监督器(VMM)
当前有很多关于“什么是虚拟机、应该如何构建虚拟机、硬件和操作系统将对构建虚拟机产 生什么影响”的研究 [1, 6, 7, 9, 12]。
本文将通过对泛第三代机器的计算机架构(computer architectures) 的分析,得出一个简单的判断一个架构是否支持虚拟机的条件。 此外,这个条件也能用于新机器的设计(machine design)过程。
虚拟机(virtual machine)是以高效、隔离的方式对真实机器(real machine)的模拟(efficient, isolated duplicate)。 我们通过虚拟机监督程序(virtual machine monitor,VMM)来解释这些概念。
1.2 VMM 特点
如图 1 所示。
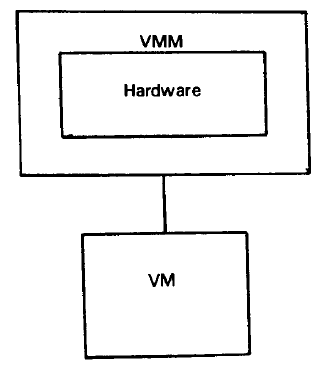
图 1. VMM
VMM 作为一个软件有三个基本特点,下面分别介绍。
1.2.1 一致性:程序在 VM 中执行与在真实机器上执行结果相同
VMM 提供了一个供程序运行的环境(即 VM),并且程序在 VM 中运行 与在真实机器上运行并无二致(essentially identical)。可能的例外是:由于系统资源不足或 时序依赖(timing dependencies)问题,程序执行效果会略有不同。
- 资源问题会出现是因为,例如,我们希望在定义中引入 VMM 有分配多片内存(对应多个 VM)的能力。
- Timing 问题是因为众多软件之间存在干扰,而且在相同硬件上并发运行着多个虚拟机。
一致的环境(identical environment)这一前提,使我们将 time-sharing 操作系统的常见行为排除在外,它们无法作为本文的 VMM。
1.2.2 高效性:大部分 VM 指令直接在硬件上执行
VMM 的第二个特点是效率(efficiency)。在这个环境下运行的软件, 最坏情况也就是执行速度略微变慢; 这就要求虚拟处理器(virtual processor)的大部分指令要直接在真实处理器(real processor)上执行, 而无须 VMM 的软件干预(software intervention)。
这一条件也直接将传统模拟器(emulators)和纯软件解释器(complete software interpreters,也称为 simulators)排除在外。
1.2.3 完全控制系统资源
第三个特点是资源控制(resource control),将常见的内存、外设等也算作资源, 虽然严格来说它们并不是处理器活动(processor activity)。
如果满足以下条件,就说 VMM 对这些资源有完全控制权:
- 在 VMM 创建的环境内运行的程序,无法访问任何未显式分配给它的资源(resource not explicitly allocated to it),以及
- 在某些条件下,VMM 能重新获取对已分配出去的资源的控制权。
1.3 虚拟机(VM)的定义
VMM 创建的环境,其实就是一台虚拟机。我们有意选取的这个定义, 不仅反映了已经广泛接受的虚拟机概念,而且还为接下来的证明了提供一个合理的环境。 在描述我们的机器模型(machine model)之前,有必要对这个这个定义做一些解释。
- 我们定义的 VMM 不一定要是一个分时系统(time-sharing system),虽然它可能是。
- 不管真实计算机上在执行什么活动,VM 中程序的执行效果要与在真实硬件上完全相同这一条件(identical effect), 使得从保护虚拟机环境(virtual machine environment)的意义上来说,隔离性(isolation)需要满足。
-
执行效果完全相同这一要求也将虚拟机(virtual machine)概念与虚拟内存(virtual memory)从本质上区分开来。
- 虚拟内存只是虚拟机的一个组成部分;分片和分页(segmentation and paging)等是具体的虚拟内存技术;
- 虚拟机实际上还会有虚拟处理器(virtual processor),及其其他虚拟设备。
接下来,在陈述和证明计算机能支持 VMM 的充分条件之前,我们先来给出 泛第三代计算机的一个正式规范。
2.1 计算机组成模块
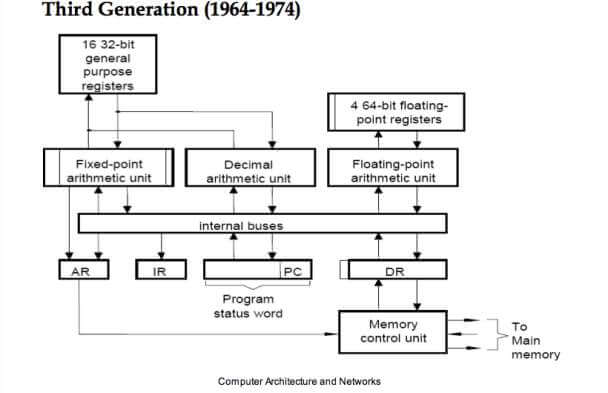
下图(原文忘了插图,下面从网上找了一张,译注)展示了一个常规第三代计算机模型的简化版,例如 IBM 360、Honeywell 6000 或 DEC PDP-10,它们有
- 一个处理器,
- 一个线性、可均匀寻址的内存
第三代计算机架构。Image credit UKDiss.com
上图几个主要模块:
- 寄存器:分为通用目的寄存器和浮点寄存器
- 处理器:分为三个处理单元:
- 定点算术单元
- 十进制算术单元!—— 对,历史上(直到现在)并不是只有二进制处理器。
- 浮点算术单元
- 内存及内存控制器
本文假设不存在 I/O 指令和中断,但二者是可以作为扩展(extensions)加进来的。 接下来我们:
- 首先提出关于这种计算机行为的几个必备假设,
- 然后描述它的状态空间(state-space),并说明状态将可能发生哪些变化。
2.1.1 处理器:supervisor/user 模式
这里的处理器是只有两种操作状态(operation mode)的常规处理器:
- supervisor 模式:处理器可执行所有类型的指令。
- user 模式:处理器只能执行部分指令。
2.1.2 内存寻址:重定位寄存器
内存寻址是根据一个重定位寄存器(relocation register)中的值做相对寻址的。
2.2 指令集
指令集包括了常见的算术、测试、分支、内存读写等指令。
需要强调的一点是:基于这些指令就能够在任意 size/key/value 的 table 上执行查找操作,然后将查到的值存储到内存中的任意位置 —— 也就是实现了 table 的查询和复制特性【注释 1】。
注释 1:后文证明过程将用到这个特性。
2.3 计算机状态表示
2.3.1 四元组表示
这种计算机的状态能用一个 4-tuple 来表示:
S = <E, M, P, R>
| | | | |
| | | | +---- relocation-bounds Register : R=(l,b), see below explanations
| | | +------- Program counter (PC) : addr of the next instruction to be executed
| | +---------- Mode (processor mode) : supervisor/user
| +------------- Executable storage (memory): size: q
|
+---- State of the real machine
R = (l, b) # Example: R=(0,q-1) corresponds to the entire physical memory
| | |
| | +--- Bound part: absolute size of the virtual memory
| +------ reLocation part: an absolute address, started from 0
|
+---------- relocation-bounds Register
-
E: 可执行内存空间
传统的 word 或 byte 寻址内存,内存的大小用
q表示。E[i]表示内存中第i个单位处的值。如果对于
0 <= i < q,都有E[i] = E'[i],那么就称E == E'。 -
M: 处理器当前的工作模式,可以是:
s: supervisor modeu: user mode
-
P: 程序计数器
P 是相对于 R 的一个地址,作为在内存 E 中的索引(index),是 接下来将要执行的指令的地址。
注意,状态 S 表示的是真实计算机系统(the real computer system)的当前状态, 而不是虚拟机的。
-
R: 重定位-边界 寄存器
R = (l, b)永远为真,不管计算机当前的状态(mode)为何。l:relocation 部分,给出的是一个绝对地址,从 0 开始;b:bound 部分,给出的虚拟内存的绝对 size(而不是最大合法地址)
例如,如果想访问所有内存,要设置
l=0 && b=q-1。
2.3.2 内存重定位(VM 地址 -> 物理地址)过程
如果一条指令要访问地址 a,那绝对地址将计算如下:
if a + l >= q # 重定位之后,(绝对地址)超出了物理内存边界
memorytrap
else if a > b # 超出了虚拟内存的边界
memorytrap
else
return E[a+l] # 真实机器的内存中 a+1 位置
后文将解释 memorytrap(内存陷入)是什么。
2.3.3 程序状态字(PSW)
S = <E, M, P, R>
| | | | |
| | | | +---- relocation-bounds Register
| | | +------- Program counter (PC)
| | +---------- Mode (processor mode)
| +------------- Executable storage
|
+---- State of the real machine
(M, P, R) 三元组通常称为程序状态字(program status word, PSW)。
为使证明方便,我们假设 PSW 能存储在单个内存位置(这个假设是很容易去掉的)。
后文将会看到为了保存执行状态,会把老 PSW 存储到 E[0] 然后从 E[1] 读取新 PSW 的操作。
2.3.4 状态的有限集合
以上四个变量都只能取有限几个值,因此 S 将是一个有限状态集合,我们称为 C。
那么,指令(instruction) i 就是一个从 C 到 C 的函数。
i: C -> C
例如,
i(S1) = S2i(E1, M1, P1, R1) = (E2, M2, P2, R2)
至此,我们讨论的所有内容还都属于常规第三代计算机的范畴,因此没什么让人惊讶的。
2.4 第三代计算机模型(核心抽象):原语保护+简单内存分配
将常规第三代计算机系统外表的复杂性去掉之后,剩下的将是
- 一个广义的围绕 supervisor/user 模式概念构建的 primitive protection system(原语保护系统,即特权指令只能被 supervisor 执行,译注),
- 也是一个围绕重定位-边界系统(relocation-bounds system)构建的简单内存分配系统。
在这个模型中,为简单起见,我们将稍微偏离最常见的重定位系统,假设在 supervisor 和 user 模式中 这种重定位都是可用的。这种偏离对我们的证明没有很大影响。 另外也要注意,处理器的所有内存引用都假设是 relocated。
这个模型的一个核心限制是:不包括 I/O 设备及相关指令。 现在大部分 extended software machine(即虚拟机)都没有提供显式的 I/O 设备及指令支持,但最近 的第三代硬件计算机已经开始支持这种功能了。 DEC PDP-11 中,I/O devices 是作为 memory ceils 来处理的,I/O 操作就是定位到对应的内存单元然后读/写适量的内存数据。
PDP-11 在计算机、操作系统和编程语言的发展历史上有极其重要的地位。
1969 年,Bell Labs 的 MULTICS 项目失败之后,Ken Thompson 在 PDP-7 上用汇编语言非正式地 开发了一个轻量级操作系统;1970 年这个操作系统移植到 PDP-11,并正式命名为 Unix 。1972 年,Dennis Ritchie 和 Ken Thompson 在 PDP-7 上用汇编实现最早的 C 语言 ,稍后又移植到 PDP-11,然后用它重写了 Unix —— 这就是 Unix 第四版。
C 语言的某些特性在今天看来有点古怪,但如果考虑一下它的诞生背景,尤其是对照 PDP-11 的架构,那很多东西就不难理解了。 例如,它的前递增(
++i)和后递增(i++)运算符都能一个萝卜一个坑地对应到 PDP-11 的不同寻址模式。更多关于编程语言和计算机架构的思考,移步: (译) C 不是一门低层(low-level)语言(acmqueue, 2018)
译注。
2.5 Traps
继续描述我们的第三代模型,接下来定义什么是 trap(一般翻译成陷入或捕获)。
2.5.1 定义
如果一条指令 i<E1,M1,P1,R1> = <E2,M2,P2,R2> 且满足下列两个条件,它就是 trap 了:
/- (M1,P1,R1), j = 0 # E2 地址空间的第一个值(E2[0]),保存系统此时的状态(PSW)
E2[j] = |
\- E1[j] , 0 < j < q # E2 地址空间的其他地方,值与 E1 完全相同
(M2, P2, R2) = E1[1] # E2 系统此时的状态,保存到 E[1] 中
解释一下:
-
当指令 trap 之后,对于内存空间来说,除了第一个地址中的内容(
E2[0])有变化,其他地址中的内容都保持不变。 换句话来说,在 trap 之前会将当前 PSW 写入第一个地址。 -
trap 之后,当前 PSW 是从内存空间的第二个地址
E1(1)读取的, 在大部分第三代机器的软件中,期望的是M2 = supervisor mode以及R2 = (0, q-1)。
2.5.2 直观解释
直观上的解释是,trap 时会自动保存机器当前的状态,然后通过改变
- 处理器模式
- 重定位-边界 寄存器
- 程序计数器(初始化为 E[1])
的值,将控制权交给一个预先指定的例程(routine)。
这个定义还可以放宽,包括 trap 不会阻塞指令,而是立即或在几条指令之后获得控制权, 只要状态是以这种可逆的方式存储的,在 trap 结束之后能精确恢复原来的执行状态。
2.5.3 Memory trap
对 trap 进行分类将给我们带来很大方便。
当一条指令给出的内存地址超出了 R 中的范围或物理内存的范围时, 就会触发 memory trap。
基于前面定义的变量,用伪代码来表示就是:
# a: address
# l: value in the relocation register
# b: relocation bounds
# q: physical memory size
if (a + l >= q) || (a >= b)
memorytrap
指令的行为是机器状态 S 的一个函数。
接下来我们根据指令行为的不同对其进行分类。 一条指令被划分到哪个类别,将决定真实机器是否可虚拟化。
3.1 特权指令(privileged instruction)与特权指令 trap
如果对于任意一对状态(state pair) S1 和 S2,都有
S1 = (e, supervisor, p, r)
S2 = (e, user , p, r)
其中,i(S1) 和 i(S2) 都不会触发 memory trap
在以上条件下,如果对于一条指令 i,都有
- i(S2) 会发生(非 memory)trap,且
- i(S1) 不会发生 trap
那么就称指令 i 是一条 privileged instruction(特权指令), 相应的 trap 称为 privileged instruction trap(特权指令陷入)。
S1 与 S2 的唯一区别是:S1 是 supervisor mode,S2 是 user mode。
通俗解释就是:在其他条件完全相同的情况下,当一条指令 工作在 supervisor 模式时不会 trap,工作在 user 模式会 trap, 那这就是一条特权指令。译注。
这种特权指令的概念与传统上还是很类似的。特权指令独立于虚拟化进程 (independent of the virtualization process),它们是机器的特性 (characteristics of the machine),阅读机器的操作说明书就能判断出来。
但注意,我们这里是根据是否 trap 来定义特权指令的。仅仅是 NOP-ing 一条指令而非 trap 它是不够的, 这种不能被称作特权指令,也许 “user mode NOP” 比较准确。
第三代计算机中的特权指令例子:
-
IBM System/360 LPSW:
if M = s # supervisor mode load_PSW else trap; -
Honeywell 6000 LBAR 和 DEC PDP-10 DATAO APR:
if M = s # supervisor mode load_R else trap
3.2 敏感指令(sensitive instructions)
另一种重要的指令类型是 sensitive instructions [4]。 这种指令在很大程度上觉得了一台计算机能否支持虚拟化。
我们定义两种类型的敏感指令。
3.2.1 控制敏感(control sensitive)指令
如果存在一个状态 S1 = <e1, m1, p1, r1>,有
i(S1) = S2 = <e2, m2, p2, r2>
其中:
1. i(S1) 不会 memory trap,且
2. (r1 != r2 || m1 != m2) == true
就称指令 i 是一条控制敏感指令。
也就是说,如果一条指令不经过 memory trap 流程就尝试修改可用内存量(r1 != r2), 或修改处理器模式(m1 != m2),那就是控制敏感的【注释 2】。
【注释 2】
Certain machines may have instructions that can store old and new PSWs directly; that is, reference e[0] or e[1], regardless of the values in the relocation register R. In that case, one might wish to add to the two control sensitivity conditions a third one: that e1[i] ~ e2[i] for i = 0,1.
例子:
- 上一节几个特权指令的例子,也都是 control sensitive 的。
- 另一个例子是 DEC PDP-10 中的
JRST 1指令,作用是返回到 user mode。
关于我们这种控制敏感型指令的定义,有几点值得注意。
-
前面定义 VMM 时,我们假设了它能完全控制系统资源。 而在我们这个第三代计算机简化模型中,内存是唯一的系统资源【注释 3】。 控制敏感指令会影响或潜在地影响 VMM 的这种控制。
【注释 3】 这里我们并没有将处理器(processor)作为一种系统资源。从最简单的形式上来说, 虚拟机概念不需要 multiprograming 或 time-sharing,因此无需控制处理器的分配。 但对大部分实际系统来说,这个假设并不准确,因此如果引入 I/O,这个假设就要改。 忽略处理器资源的分配,带来的一个有趣后果是可能允许直接执行 HALT 指令, 而在 VM time-sharing 场景下,这一行为是不允许的。
-
这里使用的是一个简化的机器模型(simplified machine), 其中没有独立的条件代码(condition codes)或允许指令之间交互的复杂东西 (所有交互都通过 PSW)。但对于实际计算机,ADD 或 DIVIDE 之类的指令在 异常条件时会 trap,这种情况下定义 control sensitivity 时就要将这些 trap 都排除在外,就像对待 memory trap 一样。
3.2.2 重定位偏移算子 ⊕
为描述第二种敏感指令,我们需要先引入一些符号。
前面已经定义了 重定位-位置 寄存器 r = (l,b)。
对于一个整数 x,定义一个算子 ⊕,使得:
也就是重定位寄存器 r 的 base 值移动了 x 个位置。
此时需要指出,
- 一个状态 S 能访问哪些内存(the only part of memory), 就由重定位-边界寄存器 R 指定的。
- 因此,要确定一条指令的效果,只需要将 R 限制的这部分内存包括到状态描述里。
- 我们用
E | R来表示这部分内存中的内容。 - 由于
r = (l,b),E | r表示的就是从l到l+b位置的这部分内存中的内容。
因此,我们本质上可以用 S = (e|r, m, p, r) 来表示一个状态【注释 4】。
【注释 4】 To be more precise, (e|r, m, p, r) represents an equivalence class of states: those whose values of m, p, and r match, and for whom that portion of memory from l to l+b is the same. To be completely accurate, it must also be the case that E[1] is also the same. In this way the equivalence classes of states are maintained . by instructions. That is, for any S1 and S2 both in the class (e|r, m, p, r) and any instruction i, where i(S1) = S1’ and i(S2) = S2’, S1’ and S2’ are also in the same equivalence class. Even though (e|r, m, p, r) really specifies a set of states rather than a single state, we will not maintain the distinction in the text since it will be clear from context that instructions behave as above.
那 E | r⊕x 又表示什么意思呢?结合以上两者,它表示的就是从 l+x 到 l+b+x 的这部分内存中的内容。
那么说 E | r == E' | r⊕x 意味着对于 0 < i < b,有 E[l+i] == E'[l+x+i]。
直观上,我们已经准备好描述程序在可执行存储中移动时的条件了。
在引入这些繁琐的符号和公式之后,我们现在终于可以定义第二种控制敏感指令了。
3.2.3 行为敏感(behavior sensitivity)指令
对于一条指令 i,如果存在一个整数 x 和两个状态,
1. S1 = (e | r , m1, p, r ), and
2. S2 = (e | r⊕x, m2, p, r⊕x),
where,
1. i(S1) = (e1 | r , m1, p1, r )
2. i(S2) = (e2 | r⊕x, m2, p2, r⊕x), and
3. i(S1) and i(S2) do not memorytrap
使下面至少一条成立:
1. (e1 | r) != (e2 | r⊕x) # 可执行内存中的内容变了(E)
2. p1 != p2 # 处理器工作模式(M)导致 P(下一条要执行的指令的地址)不同
就说它是行为敏感指令【注释 5】。
The results of this paper are still true if the definition of behavior sensitivity is restricted to the cases where m2 != supervisor_mode. Changes in instruction behavior due to relocation in supervisor mode does not affect virtual machine code, since that code is run in user mode.
以上定义比较晦涩,直观上来说,对于状态的四元组 <E, M, P, R> (或 <E|R, M, P, R>,更方便理解),
-
如果一条指令的执行效果取决于
E|R中的值 (例如它在真实内存中的位置)或处理器模式(M),那这条指令就是行为敏感的。因此在我们的模型中,行为敏感又分为两种:
- 位置敏感:指令的执行行为取决于它在真实内存(real memory)中的位置,即
E|R不同导致。例子:load physical address (IBM 360/ 67 ERA)。 - 模式敏感:指令的行为受机器模式的影响,即
M不同导致。例子:DeC PDP-11/45MVPI指令(move from previous instruction space)。 这条指令依据当前模式(mode)等信息,生成它的有效地址(P)。
- 位置敏感:指令的执行行为取决于它在真实内存(real memory)中的位置,即
-
其他两种情况,即指令执行之后, M 或 R 不同,属于控制敏感型的。
按照以上定义,如果一条指令是控制敏感或行为敏感的,那它就是敏感型的;否则就是 innocuous(无害)指令。 有了这种分类,我们就可以用更精确的术语来定义 VMM 了。
VMM 是一个特殊的软件,更具体地说,是一个具备了一些特殊功能的控制程序(control program,CP)。
我们将证明,所有满足我们所描述的几个特性的控制程序,都能用于构建指令集满足某个特殊限制的第三代计算机。
4.1 模块组成
VMM 由几个/几类模块组成。
4.1.1 第一类模块:分发器(dispatcher,D)
第一类是 dispatcher D.
D 的初始指令放在硬件会 trap 的位置:在位置 1 放置 PC(程序计数器)的值。
注意,虽然前面关于 trap 的定义中并没有说明,但某些机器会根据不同的 trap 类型而陷入到不同位置。 这种行为对我们并没有很大影响,因为 D 允许有多个“第一条”指令(entry points)。
可以认为 D 是控制程序的最外层控制模块(the top level control module), 它决定了接下来调用哪个模块,也可以唤醒下面第二类或第三类模块。
4.1.2 第二类模块:分配器(allocator,A)
第二类只有一个 member,即一个 allocator A。
分配器 A 决定提供哪些系统资源。
- 如果只有一个 VM,那 A 只需要将 VM 和 VMM 分开就行了;
- 如果有多个 VM,那 A 就要保证不会将同一系统资源(例如,同一块内存)同时分配给不同 VM。
常见的第三代计算机要有能力根据给定的资源资源表(resource tables)来构建自己的分配器</mark>**。
每当 VM 中执行到会改变这个 VM 资源的特权指令时,D 会唤醒 A。
- 在我们的简化模型中,一个有代表性的例子就是重置 R (relocation-bounds) 寄存器操作( 这会改变 VM 的可用内存大小,译注)。
- 如果将处理器当做一种资源,那需要将 halt 同样当做资源。
4.1.3 第三类模块:trap 对应的 interpreter routine(解释例程)
第三种类型可以认为是所有会 trap 的指令的解释程序,每个特权指令对应一个解 释例程(interpreter routine)。这种 routine 的目的是模拟 trapped 指令的效果。
进一步,回忆一下我们当前的表示:i(S1) = S2 表示通过指令 i,状态 S1 将映射到 S2。
现在定义 ij(S1) = S2,它表示存在
- i(S1) = S3,且
- j(S3) = S2
以此类推,指令序列 ij...k(S1) 表示的意思大家就清楚了。
4.2 控制程序(CP)的表示
令 vi 表示这样一个指令序列。那么就可以将
interpretive routines 表示为 vi 的集合,
{vi}, 1 <= i <= m
其中 m 为特权指令的数量。
dispatcher 和 allocator 也是指令序列。因此,一个控制程序(Control Program, CP)就由它的三部分表示如下:
CP = <D, A, {vi}>
我们感兴趣的是满足我们将讨论的某些特性的控制程序。 接下来将假设控制程序运行在 supervisor mode,在实际系统中,这一点是非常常见的。
这就是说,在 trap 发生时,硬件会将 PSW 加载到地址 1;此时 PSW 需要
- 将 mode 设置为 supervisor,
- 将程序计数器 PC 设置为 D 的第一个地址。
此外,我们认为其他所有程序都运行在 user mode 【注释 6】。
See for example [6, pp. 108-113] for a discussion of other alternatives to these assumptions.
trap 执行结束后,控制程序(的最后一个操作)将原来的 PSW 加载回来,在 将控制权重新交还给运行中的程序时,会将 mode 设置为 user。
因此,在控制程序中就必须有一个位置用来记录虚拟机的 simulated mode。
在控制程序监督下运行的程序,有三个特性:高效性(efficiency)、资源控制(resource control)和等价性(equivalence)。
5.1 三大特性
5.1.1 高效性(efficiency)
所有 innocuous 指令由硬件直接执行,无需控制程序的任何干预。
5.1.2 资源控制(resource control)
用户程序无法改变分配给它的系统资源,例如内存;需要修改资源时,必须唤醒控制程序的分配器 A。
5.1.3 等价性(equivalence)
任何程序 K,在控制程序的监督下执行时,其行为应当与没有控制程序监督时一致 —— 但有两个例外,
-
timing
由于来自控制程序的偶尔干预,K 中的特定指令流执行可能要(比没有控制程序干预)慢一些。 因此,如果模型中假设执行时间完全不变,可能会导致错误的结果。
在我们的简单系统中,将假设这种变慢可以忽略不计。
-
resource availability
举个例子,对于程序提出的修改重定位-边界 寄存器(即申请更多内存资源),分配器 A 无法满足;因此程序接下来的行为与资源充足时的行为就会有差异。
这种问题很容易出现,因为控制程序自身也占用内存。 我们要意识到:创建出来的 VM 环境是真实硬件的一个缩小版(”smaller” version): 逻辑上一样,但资源量要小(lesser quantity of certain resources)。
需要保证的等价性是:程序运行在 VM 中时,与运行在一台同样资源量的真实硬件机器上时,行为应当完全一致。 后文将对等价性作出更精确的描述。在此之前,先给出我们的主定理(major theorem)的定义和声明。
5.2 定理一(主定理):计算机支持 VMM 的充分条件
我们说一个 VMM 是满足三个特性(efficiency, resource control, and equivalence)的任意控制程序。 那么,功能上来说,任何程序在 VMM 存在时执行所看到的环境,就称为一台虚拟机(virtual machine)。 这个环境由真实机器(real machine)和虚拟机监视器(VMM)两部分组成。 这个正式定义与前文的直观(形象)定义是一致的。
有了这个定义,就可以声明我们的基本定理了。
THEOREM 1:对于任何常规第三代计算机,如果其敏感指令(sensitive instructions) 是其特权指令(privileged instructions)的一部分,那就能为这台计算机构建一个 VMM。
6.1 什么是“常规第三代计算机”
在讨论这定理之前,先来明确什么是“常规第三代计算机”。 这个术语用来表示所有满足前面假设的几个特性的计算机:
- 重定位机制
- supervisor/user mode
- trap 机制
这些假设简洁而合理地反映了当前第三代计算机的一些相关实践。 此外,这个术语也暗示这些指令集是足够通用的,基于这些指令能够构建
- dispatcher
- allocator
- generalized table lookup procedure:后文会看到为什么需要这个东西。
6.2 状态集合 C 和同态映射
基于这些“第三代计算机”特性,定理一提供了一个相当简单且足够保证虚拟化的条件。 其实这几个特性如今已经非常普遍,因此唯一一个新限制其实也就是敏感指令和特权指令之间的关系, 而判断这个关系是否成立也是非常容易的。
此外,这个定理还可以作为 design requirement 被硬件设计师使用。当然,我们并没有 对中断处理或 I/O 需要满足哪些条件作出说明。本质上这些也是很类似的。
将机器所有状态的集合称为 C,在证明过程中用 C 的同态映射 (homomorphism on C)来刻画等价性(equivalence)比较方便。
将 C 分为两部分:
- Cv :VMM 已经在内存和 PSW 的 P 中提供的状态,其中 PSW 就是内存第一个地址处存储的值,也是 VMM 的第一个地址。
- Cr :所有其他状态。
这两个集合分别反映了真实机器有 VMM 和无 VMM 条件下的所有可能状态。
每条指令都可以认为是一个状态集合 C 之上的一元算子(unary operator):
i(Si) = Sk
同理,每个指令流(instruction sequence),例如
en(S1) = ij...k(S1) = S2
也可以认为是 C 之上的一个一元算子。
6.3 虚拟机映射(VM map)
考虑有限长度的所有指令流,将这种指令流集合用 I 表示。I 包含了同态映射要用的算子。
定义一个虚拟机映射(VM map)
f:Cr -> Cv
是一一同态映射(one-one homomorphism),对于指令流集合 I 中的所有算子 ei 都成立。
也就是说,对于任意状态 Si ∈ Cr 和任意指令流 ei, 存在一个治理流 ei’ 满足
f(ei(Si) = ei'(f(Si))
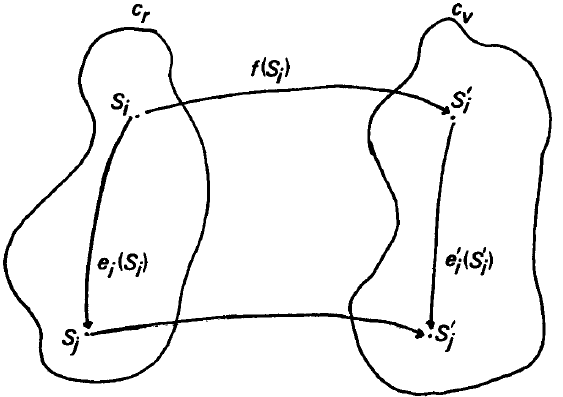
如图 2 所示。
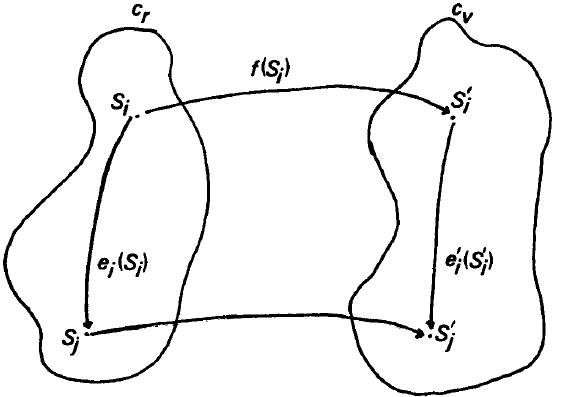
图 2. VM map
VM map 定义中有两个相关联的特性:
-
从 real machine 的状态到 virtual machine 的状态的某个特定映射,在数学上存在的。 但这里并没有对构建这种映射的能力、用硬件还是软件来构建,做出任何限制。
-
Cv domain 的 ei’ 指令是真实存在的,对应的是 Cr domain 的 ei 指令流。
我们要求
- 作为 VM map 定义的一部分,对于每个 ei,存在合适的 ei’ 且能被执行。因此不是立即清楚,对于一个特定计算机,VM map 是否存在。
- 作为定义的一部分,还需要指出,f 是一一映射。这个条件等价于 f 是(左)可逆的,将其逆函数称为 g,后文的证明中将用到。
为更清楚地展示这个概念,我们来看一个具体的 VM map。
6.4 VM map 示例
令:
-
控制程序占据物理内存的前 k 个位置,也就是说:
- E[0] and E[1] 是 PSW 预留的
- 控制程序占据
2 ~ k-1位置。
-
接下来的 w 个位置给虚拟机使用,此处有
k + w <= q,即不能超越物理内存边界。
因此,f(E, M, P, R) = (E', M', P', R'),其中 S = (E, M, P, R) 是没有 VMM 的机器的状态。
我们假设在这样一台真实机器(接下来将拿虚拟机的活动和它做对比)上,r = (1,b) 中,b 的值永远小于 w。
- E’[i] = the control program, for i = 2 ~ k-l,即控制程序占用内存的前 k 个位置
- E’[i + k] = E[i], for i= 0, w-1,物理内存中 (k, k+w-1) 位置,即 VM 占用的物理内存
-
E’[i] = (m’,p’,r’),
- m’ = supervisor,即模式永远是 supervisor
- p’ = first location of the control program,控制程序的起始地址
- r’ = (0,q-1),完整的物理内存空间
- E’[0] = <m,p,r> as last set by trap handler,表示 PSW,由 trap handler 设置
- M’ = u (user),
- P’ = p,
- R’ = (l+k, b), where R = (l, b).
需要说明,以上 VM map 只对真实机器中一条指令执行结束且下一条指令还没开始时的状态 (states after the completion of one instruction in the real machine and before the beginning of the next)做映射。
这个 VM map 的例子非常简单;当然可以创建更加复杂的函数来表示 VM map 所需的特性, 但我们接下来还是将用以上例子,并把它作为标准 VM map。如无特殊说明,接下来提到的 VM map 都是这个标准 VM map。
Fig. 2. The virtual machine map.
6.5 等价性(equivalence)意味着什么
现在我们来声明 “equivalence”,或者更准确地说,”essentially identical effect” 意味着什么。
假设有两台机器,一个在状态 S1,一个在状态 S1’ = f(S1),二者同时开始运行, 那么,当且仅当对于任何状态 S1,如果真实机器在 S2 状态 halt 了,那 VM 一定在状态 S2'=f(S2) halt 。 那么我们就称 VMM 提供的环境与真实计算机是等价的。
这里说的 VM halt,意思是在 VM 系统中,用户程序试图从位置 j(其中 j>k)执行一个 halt 操作。
这个定义的设定有多方面考虑:
- 基于比较点(comparison points)而非已执行指令的数量(number of instructions executed)触发 halt, 例如,部分指令会被 VM 系统解释执行(interpreted),因此可能会使用很长的指令流,基于指令数量就不合适。
- 这里选择的 VM map f(S21) = S2 非常简单,映射关系一目了然,因此无需笔墨,大家就能看出 逆函数 g(S2’) = S2 是成立的,即等价性存在。
6.6 定理一的简要证明(Proof Sketch)
我们的目标是证明:只要计算机满足前面分析的 equivalence、resource control 和 efficiency 这三个特性,就能为这种计算机构建控制程序(即 VMM)
控制程序
We construct a control program that obeys the three requisite properties. It is the cp outlined earlier. The only constructive part not demonstrated was the ability to provide the appropriate interpretive routines for all privileged instructions. We demonstrate below that a general solution exists. Note that this will be an existence argument only. In practice there are much more practical techniques. 任何 privileged instruction(实际来说,**任何指令)的执行结果只取决于
M, P, R, E[1]E|R
也就是说,不是所有内存,而仅仅是位置 1 以及重定位-边界寄存器 R 限定的内存范围。 再考虑到:
- VM 最大可用的内存空间是
E|R = w
那任何特权指令就能够以 two-tuples 方式组织到一张表里面,表的长度就是 <E|R, M, P, R> 的所有可能状态。
这个二元组的两个元素:
- 第一个元素:某个状态
- 第二个元素:在 1 中的状态下,执行某个特权执行的结果(effect)
但这样一张表会非常庞大,而且对于每个特权指令,都需要建立一张这样的表。最终结果就是 VMM —— 用它占用的内存空间 (0, k-1) 来衡量, 就会非常庞大。那么,无需数学证明,我们就可以得出的一个结论是:通过限制真实机器的大小 —— 具体来说就是 w 的大小 —— 我们就可以限制这个表的大小。
We have assumed that third generation machines have an instruction set capable of managing these tables. Hence, interpretive routines are guaranteed constructable. Note of course that such state tables are a last resort, for those privileged instructions of an extremely arcane nature which are in fact arbitrary algorithms.
By limiting the size of “real” memory though, the number of nonequivalent such programs is also limited, hence the appropriate tables are also of limited size. In all real cases today, much simpler and more efficient routines exist, and should be used.
This completes the description of the control program, so it remains to discuss the three properties.
三个特性
Guarantees of the resource control and efficiency properties are trivially dispensed with. By the definition of sensitive instruction and the subset requirement of the theorem, any instruction that would affect the allocation of resources traps and passes control to the VMM. Efficiency has been taken to mean the direct execution of innocuous instructions; we have constructed the VMM to provide that behavior.
Only equivalence remains. It is necessary to demonstrate that, for any instruction sequence t = ij . . . k where k is a halt and any state S1 of a real machine, the following is true.
Let S1’ = f(S1) and S2 = t(S1). Thenf(S2) = t(S1’).
Again, see Figure 2.
First, we demonstrate that the equivalence property is true for single instructions; that is, for t = any instruction i. We consider two cases, innocuous instructions and sensitive instructions. Both cases are easy, and demonstrated in detail in the Appendix as lemmas 1 and 2. The innocuous case follows from the definition of an innocuous instruction and direct application of the definition of VM map. The sensitive case follows from the fact that all sensitive instructions are privileged, from the existence of correct interpretation sequences and the VM map definition.
Since single instructions “execute correctly,” it now remains only to show that finite sequences also do.
That is for any instruction sequence em = ij . . . k, em(f(S)) = f(em‘(S)). This fact follows from lemmas 1 and 2, and the definition of the VM map f as a one-one homomorphism. It is a fairly standard proof and is demonstrated in the Appendix as lemma 3.
The proof is now complete, since for third-generation- like machines in which sensitive instructions are a subset of privileged instructions, we have demonstrated that a control program can be constructed which obeys the required three properties. That is, we have exhibited a VMM. Q.E.D.
充分而非必要条件
注意,有几方面原因导致定理一的必要条件在通常情况下并不成立。 也就是说,在某些条件下,即使定理一的前提并不满足,仍然能为一台计算机构建出 VMM。
As a case in point, architectures that include location sensitive instructions may still support a virtual machine system if it is possible to construct a VMM that resides in high core, letting other programs execute unrelocated. Location sensitivity then would not matter.
In addition, there may be instructions that are not true privileged instructions as defined earlier, but which still trap when an undesirable action would result. An example of such a case is an instruction that is able to change the relocation bounds register, but can only decrease the bounds value when executed from user mode.
基于定理一,我们很快就能引申出很多相关结果,例如递归虚拟化 (recursive virtualization,或称嵌套虚拟化)的设想:是否有可能在 VM 内运行一个 VMM 副本,这个副 本的行为与创建这个 VM 的 VMM 特性完全一样?如果这个过程可以重复,直到系统资源耗 尽(因为控制程序需要消耗一些内存资源),那就称这台机器是可递归虚拟化的( recursively virtualizable)[2, 6]。
7.1 定理二:递归虚拟化的充分条件
THEOREM 2. 一个常规第三代计算机是可递归虚拟化的,如果:
- 这台计算机支持虚拟化(virtualizable),且
- 可在这台计算机上构建一个没有任何 timing 依赖的 VMM。
7.2 定理二的证明
证明. This property is nearly trivial to demonstrate. A VMM is guaranteed, by definition, to produce an environment in which a large class of programs run with effect identical to that on the real machine. Then it is merely necessary to demonstrate that a VMM which belongs to that class of programs can be constructed. If it can, then the performance of the VMM running on the real machine and under other VMMS will be indistinguishable.
The only programs excluded from the class of identically performing programs are those which are resource bound, or have timing dependencies. The second limitation is mentioned in the statement of the theorem. The resource bound for our skeletal model is only memory, and it just limits the depth (number of nested VMMS) of the recursion, as pointed out in the definition of recursive virtualization. Hence the VMM as constructed earlier qualifies as a member of that “large class of programs.” Q.E.D.
前面提到,目前只有很少的第三代架构能够虚拟化 [5,6]。 出于这个原因,我们放松前面的定义,得到一个更加宽松、通用但略低效的定义, 对应的模型我们称为 hybrid virtual machine system (HVM) [6]。
8.1 HVM 定义:更多指令通过软件解释执行
HVM 的结构与 VMS(virtual machine system)几乎完全相同, 区别在于:更多的指令是解释执行的,而不是直接在硬件上执行的。 因此 HVM 效率要比 VM 低,但好处是,实际中更多的第三代架构是满足这个模型的。 例如,PDP-10 can host a HVM monitor, although it cannot host a VM monitor [3].
放松定义,需要将敏感指令划分为两个 not necessarily disjoint subsets.
8.2 对敏感指令进一步分类
user sensitive
An instruction i is said to be user sensitive if there exists a state S = (E, u, P, R) for which i is control sensitive or behavior sensitive.
That is, an instruction i is user control sensitive if the definition given earlier for control sensitivity holds, with ml in that definition set to user. The instruction i is user behavior sensitive if the definition for location sensitivity holds with the mode of states S1 and S2 equal to user. Then i is user sensitive if it is either user control sensitive or user location sensitive. Intuitively, these are instructions which cause difficulty when executed from user mode.
supervisor sensitive
In a parallel fashion, an instruction i is supervisor sensitive if there exists a state S = (E, s, P, R) for which i is control sensitive or behavior sensitive.
8.3 定理三
THEOREM 3. A hybrid virtual machine monitor may be constructed for any conventional third generation machine in which the set of user sensitive instructions are a subset of the set of privileged instructions.
In order to argue the validity of the theorem, it is first necessary to characterize the HVM monitor. The difference between a HVM monitor and a VMM is that, in the nVM monitor, all instructions in virtual supervisor mode will be interpreted. Otherwise the HVM monitor is the same as the VM monitor. Equivalence and control can then be guaranteed as a result of two facts. First, as in the VMM, the nVM monitor always either has control, or gains control via a trap, whenever there is an attempt to execute a behavior sensitive or control sensitive instruction. Second, by the same argument as before, there exist interpretive routines for all the necessary instructions. Hence, all sensitive instructions are caught by the HVM and simulated.
To aemonstrate the utility of the concept of a HVM monitor, we present the following.
Example. The PDP-10 instruction JRST 1, (return to user mode) is a supervisor control sensitive instruction which is not a privileged instruction. Hence the PDP-10 cannot host a VMM. However, since all user sensitive instructions are privileged, it can host a hybrid virtual machine monitor [3].
本文提出了一种第三代计算机系统的规范化(或正式)模型。 基于这个模型,我们推导出了判断一个特定的第三代计算机是否能支持 VMM 的必要和充分条件。
前期研究 [4, 5] 已经指出了第三代机器的虚拟化所需的架构特性, 而我们基于本文提出的规范化方法,建立了评估这一问题的更加精确的机制及所需满足的条件。 这些结果已经用在 UCLA,例如,评估 DEC PDP-11/45 以及对它做出修改,这样就能建立一个虚拟机系统[13]。
虽然这个模型确实抓住了第三代计算机的本质,但出于展示目的,其中一些地方做了简化。 从经验上来说,我们认为该模型缺失的东西,例如 I/O 资源和指令、异步事件、或更加复杂的内存映射机制, 能作为这个基础模型的直接扩展(extensions)加入进来[6, 12]。
另外,近期计算机系统架构领域的一些工作已经提出了一些无需传统 VMM 解释软件(interpretive software)开销, 直接支持虚拟机的虚拟化架构提案[2, 6, 8, 10, 11]。 本文提出的方法,可能也能用于验证他们提出的架构及其是否能支持虚拟化。
致谢
The authors would like to thank their colleagues at both UCLA and Harvard for many helpful discussions on various aspects of virtual computer systems. Special thanks are due to Professor G. Estrin of tJCLA and Dr. U.O. Gagliardi of Harvard University and Honeywell Information Systems for their advice and encouragement during the preparation of this paper. In addition, the authors wish to thank the referees for their constructive comments on an earlier draft of this paper.
Several results were used in the statement of the proof without being explicitly demonstrated. They are the lemmas which follow.
LEMMA 1. Innocuous instructions, as executed by the virtual machine system, obey the equivalence property. PROOF SKETCH. Let i be any innocuous instruction.
Let S be any state in the real machine, and S’ = f(S). S = (e|r, m, p, r) and S’ = (e’ [ r’, m’, p’, r’). However, from the definition off, e’|r’ = e | r and p’ = p, and the bounds in both r’ and r are the same. By definition, i(S) cannot depend on m or 1 (the relocation part of r), and all other parameters are the same for both S and S’.
Hence it must be the case that i(S) = i(S’). Q.E.D.
LEMMA 2. Sensitive instructions, as interpreted by the virtual machine system, obey the equivalence property.
PROOF SKETCH. By assumption, any sensitive instruction i traps. By construction, the interpretation is done correctly, given all necessary parameter specifications. The values of locations E I R are not changed by the trap. The values of P and R are saved in El0].
The “simulated mode” value M is stored by the VMM. Hence all necessary information is present, so proper interpretation can be performed. Q.E.D.
LEMMA 3. Given that all single instructions obey the equivalence property, any finite sequence of instructions also obeys the equivalence property.
PROOF. The proof is by induction on the length of the instruction sequence. Each sequence can be thought of as a unary operator on the set C of states. The basis of the lemma is true by the hypothesis in the statement of the lemma.
In the following, parentheses will be used only sparingly. Hence f(g(h(S))) may be written fgh(S). Induction Step. Let i be any instruction, and t any sequence of length less than or equal to k, and t’ the instruction sequence corresponding to t.
Then by the induction and lemma hypothesis, we have that, for any state S, there exists an instruction sequence t’ such that f(t(S)) = t’(f(S)) and f(i(S)) = i’(f(S)) where the primed operators may or may not be the same instructions or sequences as the unprimed operators. The instruction sequences may differ since some of the instructions expressed by the unprimed operators may be sensitive. The primed operator includes the interpretation sequences for those instructions. We are given
f t ( s ) = t’f(s). (1)
Clearly then,
i’ft(S) = i’t’f(S). (2)
But, for any S, we are given
i’f(S) = fi(S). (3)
So, letting t(S) in (2) be S in (3), we have, combining
(3) with the left side of (2):
fit(S) = i’t’f(S).
Since the sequence may be any sequence of length k + 1, and the above is the desired induction step result, the lemma is proven. Q.E.D.
- Buzen, J.P., and Gagliardi, U.O. The evolution of virtual machine architecture. Proc. NCC 1973, AHPS Press, Montvale, N.J., pp. 291-300.
- Gagliardi, U.O., and Goldberg, R.P. Virtualizable architectures, Proc. ACM AICA lnternat. Computing Symposium, Venice, Italy, 1972.
- Galley, S.W. PDP-10 Virtual machines. Proc. ACM SIGARCH-SIGOPS Workshop on Virtual Computer Systems, Cambridge, Mass., 1969.
- Goldberg, R.P. Virtual machine systems. MIT Lincoln Laboratory Rept. No. MS-2686 (also 28L-0036), Lexington, Mass., 1969.
- Goldberg, R.P. Hardware requirements for virtual machine systems. Proc. Hawaii hlternat. CoJ~lbrence on Systems Sciences, Honolulu, Hawaii, 1971.
- Goldberg, R.P. Architectural principles for virtual computer systems. Ph.D. Th., Div. of Eng. and Applied Physics, Harvard U., Cambridge, Mass., 1972.
- Goldberg, R.P. (Ed). Proc. ACM SIGARCH-SIGOPS Workshop on Virtual Computer Systems, Cambridge, Mass., 1973.
- Goldberg, R.P. Architecture of virtual machines. Proc. NCC 1973, AFIPS Press, Montvale, N.J., pp. 309-318.
- IBM Corporation. IBM Virtual Machine Facility/370: Planning Guide, Pub. No. GC20-1801-0, 1972.
- Lauer, H.C., and Snow, C.R. Is supervisor-state necessary? Proc. ACM AICA lnternat. Computing Symposium, Venice, Italy, 1972.
- Lauer, H.C., and Wyeth, D. A recursive virtual machine architecture. Proc. ACM SIGARCH-SIGOPS Workshop on Virtual Computer Systems, Cambridge, Mass., 1973.
- Meyer, R.A., and Seawright, L.H. A virtual machine timesharing system. IBM Systems J. 9, 3 (1970).
- Popek, G.J., and Kline, C. Verifiable secure operating system software. Proc. NCC 1974, AFIPS Press, Montvale, N.J., pp. 145-151.
如有侵权请联系:admin#unsafe.sh