0.前言

在护网的过程中，经常需要反向连接，就有可能连接到域名上，所以可以做一个识别，判断是不是一些APT组织通过一些批量的代码生成的恶意域名。

1.朴素贝叶斯

朴素贝叶斯算法原理：其实朴素贝叶斯方法是一种生成模型，对于给定的输入x，通过学习到的模型计算后验概率分布P ，将后验概率最大的类作为x的类输出。

举个例子，a : 1(a的值是1) 对应的标签是0，a的值是1那么标签为0的概率是多少？

优点：朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。 对小规模的数据表现很好，能个处理多分类任务，适合增量式训练，对缺失数据不太敏感，算法也比较简单，常用于文本分类。

缺点：理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率，但是实际上并非总是如此，这是因为 朴素贝叶斯模型给定输出类别的情况下，假设属性之间相互独立，也就是数据得是离散的，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。而在属性相关性较小时，朴素贝叶斯性能最为良好。

需要知道先验概率，且先验概率很多时候取决于假设，假设的模型可以有很多种，因此在某些时候会由 于假设的先验模型的原因导致预测效果不佳。

由于是通过先验和数据来决定后验的概率从而决定分类，所以分类决策存在一定的错误率。 对输入数据的表达形式很敏感。

1.高斯贝叶斯分类器： 在高斯朴素贝叶斯中，每个特征都是连续的，并且都呈高斯分布。高斯分布又称为正态分布。 GaussianNB 实现了运用于分类的高斯朴素贝叶斯算法。特征的可能性(即概率)假设为高斯分布。

2.多项式贝叶斯分类器： 实现服从多项分布数据的贝叶斯算法，是一个经典的朴素贝叶斯在文本分类中使用的变种，其中的数据是通常表示为词向量的数量，虽然 TF-IDF 向量在实际项目中表现得很好。

3.伯努利贝叶斯分类器：实现了用于多重伯努利分布数据的朴素贝叶斯训练和分类算法，即有多个特征，但每个特 征 都假设是一个二元变量。 因此，这类算法要求样本以二元值特征向量表示；如 果样本含有其他类型的数据， 一个 BernoulliNB 实例会将其二值化（取决于 binarize 参数）。

先验概率

先验概率是指在没有任何额外信息的情况下，事件发生的概率。在贝叶斯分类器中，先验概率通常表示 为类别的先验概率，即在没有观察到任何特征的情况下，某个类别发生的可能。

from collections import Counter
# 假设我们有一个标签列表
labels = ["cat", "dog", "cat", "dog", "dog", "cat"]
# 计算先验概率
label_counts = Counter(labels)
total_samples = len(labels)
priors = {label: count / total_samples for label, count in label_counts.items()}
print("Prior probabilities:", priors)

提前看标签的分布，那么整个数据里面先验概率猫占比50％，狗占比50％。

没有任何的数据，也没有任何特征，就只有个标签做一个统计。

后验概率

后验概率是在给定一些观察结果后，事件发生的概率。在贝叶斯分类器中，后验概率 p(ci | x)P(Ci | X) 表示在观察到特征 xX 的情况下，类别 ciCi 发生的概率。

import numpy as np
# 假设我们有特征的概率分布
# 特征x的概率在类别Ci下
p_x_given_c = {
"cat": {"feature1": 0.7, "feature2": 0.2},
"dog": {"feature1": 0.3, "feature2": 0.8}
}
# 计算后验概率
def calculate_posterior(features, priors, p_x_given_c):
posteriors = {}
for label, prior in priors.items():
likelihood = np.prod([p_x_given_c[label].get(f, 1.0) for f in features]) 
# 使用features列表中的f
joint_probabilities = {}
for lab in priors.keys():
joint_prob = np.prod([p_x_given_c[lab].get(f, 1.0) for f in 
features])  # 计算每个类别的联合概率
joint_probabilities[lab] = joint_prob * priors[lab]
# 计算归一化常数P(x)
p_x = sum(joint_probabilities.values())
# 使用归一化常数计算后验概率
posterior = (likelihood * prior) / p_x if p_x > 0 else 0
posteriors[label] = posterior
return posteriors
# 观察到的特征
x = ["feature1", "feature2"]
# 计算后验概率
posteriors = calculate_posterior(x, priors, p_x_given_c)
print("Posteriors:", posteriors)

联合概率

联合概率是指多个事件同时发生的概率。在朴素贝叶斯中，我们假设特征之间相互独立，因此可以计算特征的联合概率。

# 计算联合概率
def calculate_joint_probability(features, p_x_given_c):
joint_probabilities = {}
for label, feature_probs in p_x_given_c.items():
joint_prob = 1
for feature in features:
feature_prob = feature_probs.get(feature, 1)  # 特征不存在时，概率为1
joint_prob *= feature_prob
joint_probabilities[label] = joint_prob
return joint_probabilities
# 计算联合概率
joint_probs = calculate_joint_probability(x, p_x_given_c)
print("Joint probabilities:", joint_probs)

DGA

恶意域名批量生成 生成的域名都有类似的规律。

1. 长度

2. 特殊字符的使用 数量、位置。

3. 熵

4. 数字与字母结合的规律，几个数字与几个字符。

2.使用朴素贝叶斯识别恶意域名

首先收集一些APT组织生成的恶意域名。

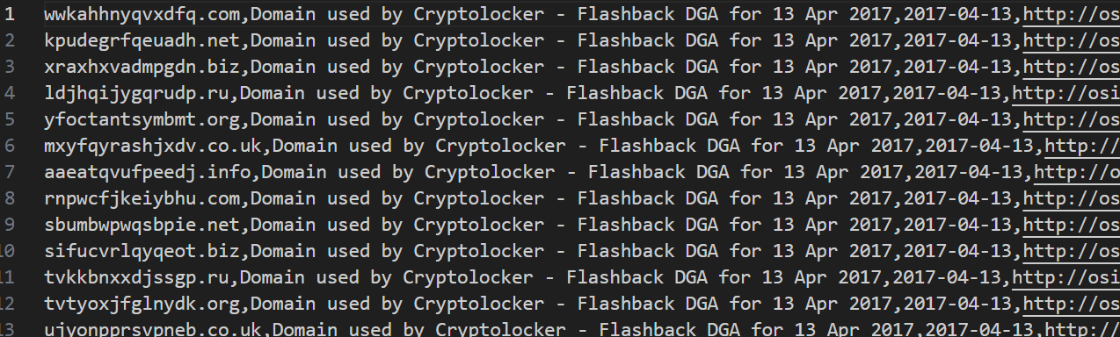
长度都是差不多的，随机生成的，这些是黑域名，那肯定就有白域名了。

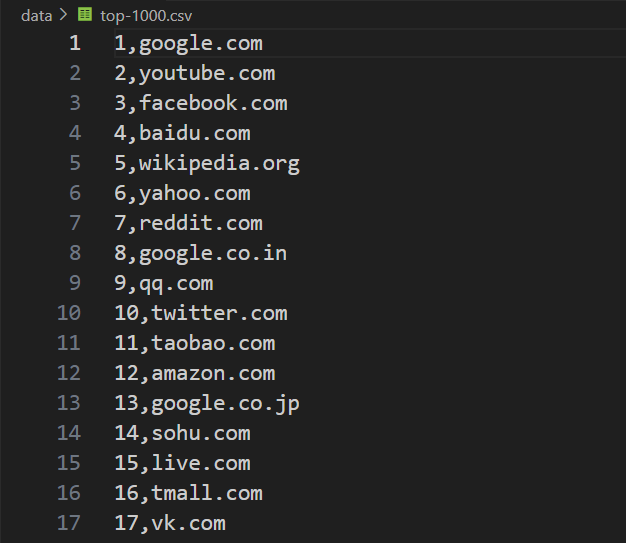
数据收集完之后就可以先来加载数据。

import csv
import numpy as np
#处理域名的最小长度
MIN_LEN=10
​
def load_alexa(filename):
domain_list=[]
csv_reader = csv.reader(open(filename))
for row in csv_reader:
domain=row[1]
if len(domain) >= MIN_LEN:
domain_list.append(domain)
return domain_list
​
def load_dga(filename):
domain_list=[]
#xsxqeadsbgvpdke.co.uk,Domain used by Cryptolocker - Flashback DGA for 13 Apr 2017,2017-04-13,
# http://osint.bambenekconsulting.com/manual/cl.txt
with open(filename) as f:
for line in f:
domain=line.split(",")[0]
if len(domain) >= MIN_LEN:
domain_list.append(domain)
return  domain_list
​
x1_domain_list = load_alexa("../data/top-1000.csv")
x2_domain_list = load_dga("../data/dga-cryptolocke-1000.txt")
x3_domain_list = load_dga("../data/dga-post-tovar-goz-1000.txt")
x_domain_list=np.concatenate((x1_domain_list, x2_domain_list,x3_domain_list))
​
y1=[0]*len(x1_domain_list)
y2=[1]*len(x2_domain_list)
y3=[2]*len(x3_domain_list)
​
y=np.concatenate((y1, y2,y3))
print(x_domain_list)

过滤掉小于10个字符的域名，毕竟APT组织生成的域名都不会小于10个字符的。

【----帮助网安学习，以下所有学习资料加v~x：YJ-2021-1，备注“freebuf”获取！】

① 网安学习成长路径思维导图
② 60+网安经典常用工具包
③ 100+SRC漏洞分析报告
④ 150+网安攻防实战技术电子书
⑤ 最权威CISSP 认证考试指南+题库
⑥ 超1800页CTF实战技巧手册
⑦ 最新网安大厂面试题合集（含答案）
⑧ APP客户端安全检测指南（安卓+IOS）

将读到的域名添加到列表中去，然后把所有的列表做一个组合。

然后给每一个数据打上标签，正常样本 0 恶意样本 1 2 。

然后把这些字符串转化为数学上可以表达的东西。

import pickle
import load_data
from sklearn.feature_extraction.text import CountVectorizer
import numpy as np
​
cv = CountVectorizer(ngram_range=(2, 2), decode_error="ignore",
token_pattern=r"\w", min_df=1)
x= cv.fit_transform(load_data.x_domain_list).toarray()
​
np.savetxt("../model/data_x.csv", x, delimiter=",")
np.savetxt("../model/data_y.csv", load_data.y, delimiter=",")
with open('../model/cv.pickle','wb') as f:
pickle.dump(cv,f) #将训练好的模型clf存储在变量f中，且保存到本地

使用CountVectorizer将字符串转化为词袋集，然后看其出现的频率和频次。

然后将数据丢给fit_transform分类器，再将其转换为numpy一维矩阵。

数据处理完就该到模型部分了。

from sklearn.naive_bayes import GaussianNB
import model_param
clf = GaussianNB(priors=model_param.nb_param["priors"],var_smoothing=model_param.nb_param["var_smoothing"])

模型结构用的高斯朴素贝叶斯。

模型训练

from sklearn.model_selection import train_test_split
import numpy as np
import model_struct
import pickle
x = np.genfromtxt("data_x.csv",delimiter=",")
y = np.genfromtxt("data_y.csv",delimiter=",")
x_train, x_test , y_train, y_test = train_test_split(x, y, test_size = 0.3)
save_model = model_struct.clf.fit(x_train,y_train)
# 模型的保存
with open('nb.pickle','wb') as f:
pickle.dump(save_model,f) #将训练好的模型clf存储在变量f中，且保存到本地

模型测试

import pickle
from sklearn.model_selection import cross_val_score
import numpy as np
import matplotlib.pyplot as plt
with open('../nb.pickle', 'rb') as f:
clf_load = pickle.load(f)  # 将模型存储在变量clf_load中
​
x = np.genfromtxt("../data_x.csv",delimiter=",")
y = np.genfromtxt("../data_y.csv",delimiter=",")
​
# 交叉验证
​
scores = cross_val_score(clf_load, x, y, cv=10, scoring='accuracy')
# 11111
# 00001
print(scores.mean())
plt.bar(np.arange(10),scores,facecolor='yellow',edgecolor='white') # +表示向上显示
for x,y in zip(np.arange(10),scores):
plt.text(x,y+0.05, '%.2f' % y,ha='center',va= 'bottom') # '%.2f' % y 保留y的两位小数 ha='center' 居中对齐 va= 'bottom' 表示向下对齐 top向上对齐
plt.ylim(0,1.1)
plt.show()

模型测试结果：

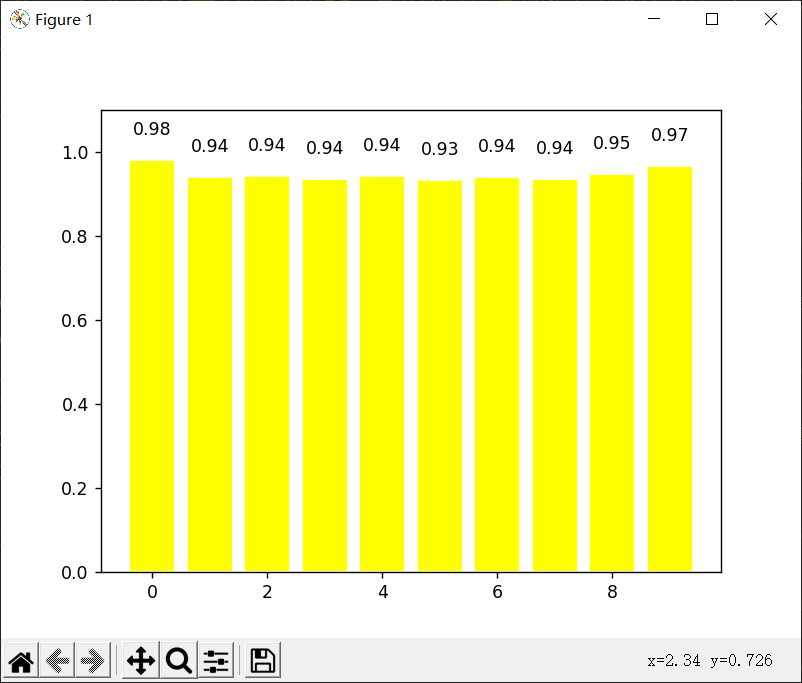
每一次运算的得分，整体的正确率在94.7％。

使用测试：

import sys
import config
sys.path.append(config.syspath)
import config
import pickle
import numpy as np
from sklearn.feature_extraction.text import CountVectorizer
​
def load_and_vec_data():
content = input("请输入要识别的域名：")
input_data = [str(content)]
with open('../cv.pickle', 'rb') as cv:
cv = pickle.load(cv)
x= cv.transform(input_data).toarray()
print(x)
return x
# 加载模型
with open('../nb.pickle', 'rb') as f:
clf_load = pickle.load(f)
​
# 使用模型进行预测
prediction = clf_load.predict(load_and_vec_data())
print("预测结果:", prediction)

输入域名，转换成数组，加载分类器。

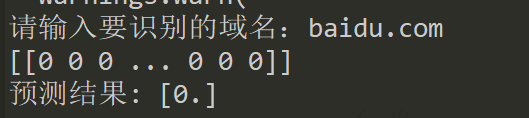
可以看到实现了正常域名和恶意域名的识别分类。

做一个可视化出来。

from flask import Flask, render_template, request, redirect, url_for
import predict_data_vec
import pickle
app = Flask(__name__, static_url_path='/static')
​
@app.route('/')
def index():
return render_template('index.html')
​
@app.route('/process', methods=['POST'])
def process():
user_input = request.form['text_input']
# 这里可以添加你的处理逻辑
x = predict_data_vec.load_and_vec_data(user_input)
# 加载模型
with open('../model/nb.pickle', 'rb') as f:
clf_load = pickle.load(f)
​
# 使用模型进行预测
prediction = clf_load.predict(x)
if prediction == [0.]:
prediction = '合法域名'
# 放过
else:
prediction = '非法域名'
result = "处理结果: " + str(prediction)  # 示例处理逻辑
return redirect(url_for('result', result=result))
​
@app.route('/result/<result>')
def result(result):
return render_template('result.html', result=result)
​
if __name__ == '__main__':
app.run(debug=True)

使用flask框架。

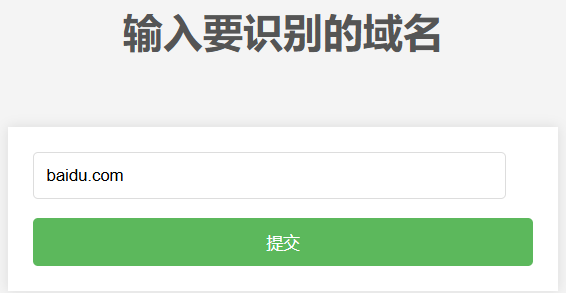
这里其实还是存在数据不足的问题，会导致模型精确度不够。

所以还是要主动去搜集恶意域名，得有个几十万数据可能才能够让模型有97％的准确率。

如果觉得还是不够稳，可以在AI判断完之后再添加个人工判断，AI觉得是非法域名，可以弹个窗或者发个消息通知。

用人的方式去理解到底是不是恶意域名，就是告警处理。