本文介绍了一个使用强化学习训练井字棋AI的项目,通过一个简单的神经网络实现人机对战。项目仅用400行C代码完成,无需外部依赖,展示了强化学习在零先验知识条件下的学习能力。 2025-3-20 00:0:0 Author: arthurchiao.github.io(查看原文) 阅读量:0 收藏
Published at 2025-03-20 | Last Update 2025-03-20
本文解读 2025 年的一个练手项目 Tic Tac Toe with Reinforcement Learning。
这个项目实现了一个非常简单的神经网络(Neural Network), 然后通过强化学习(Reinforcement Learning)训练它玩井字棋,训练好之后就可以人机对战,效果很不错。 整个项目只用了400 行左右 C 代码,没有任何外部依赖。 由于代码足够简单,非常适合用来理解神经网络和强化学习。

Fig. A simple neural network for reinforcement learning in this post
Code and scripts used in this post: Github.
传播知识,尊重劳动,年满十八周岁,转载请注明出处。
- 1 引言
- 2 运行效果
- 3. 公共代码
common.h - 4 训练代码
train.c - 5 人机对战代码
play.c - 6 延伸思考
The only winning move is not to play
本文展示了强化学习在没有任何先验知识的情况下学习新事物的能力:
- 冷启动:神经网络的权重是随机初始化的;
- 零先验知识学习:除了以下基本游戏规则,程序中没有关于游戏的知识:
- X 或 O 只能放到空格子中;
- 当一行中有三个 X 或三个 O 时,相应的一方胜出;
- 当所有的格子都被使用时,平局。
- 训练神经网络的唯一信号是游戏的奖励:胜、平、负。
1.1 井字游戏(tic-tac-toe)

Fig. A completed game of tic-tac-toe. Image Source
井字游戏是一种非常简单的棋盘游戏,可以理解成是五子棋的简化版(“三子棋”):
- 在一个 3x3 的棋盘上,两个人轮流在空白的位置下子(一般分别用 X 和 O 表示),
- 谁先将自己的三个子连成一条线(横竖斜都可以)就算赢了。
1.2 神经网络:祛魅
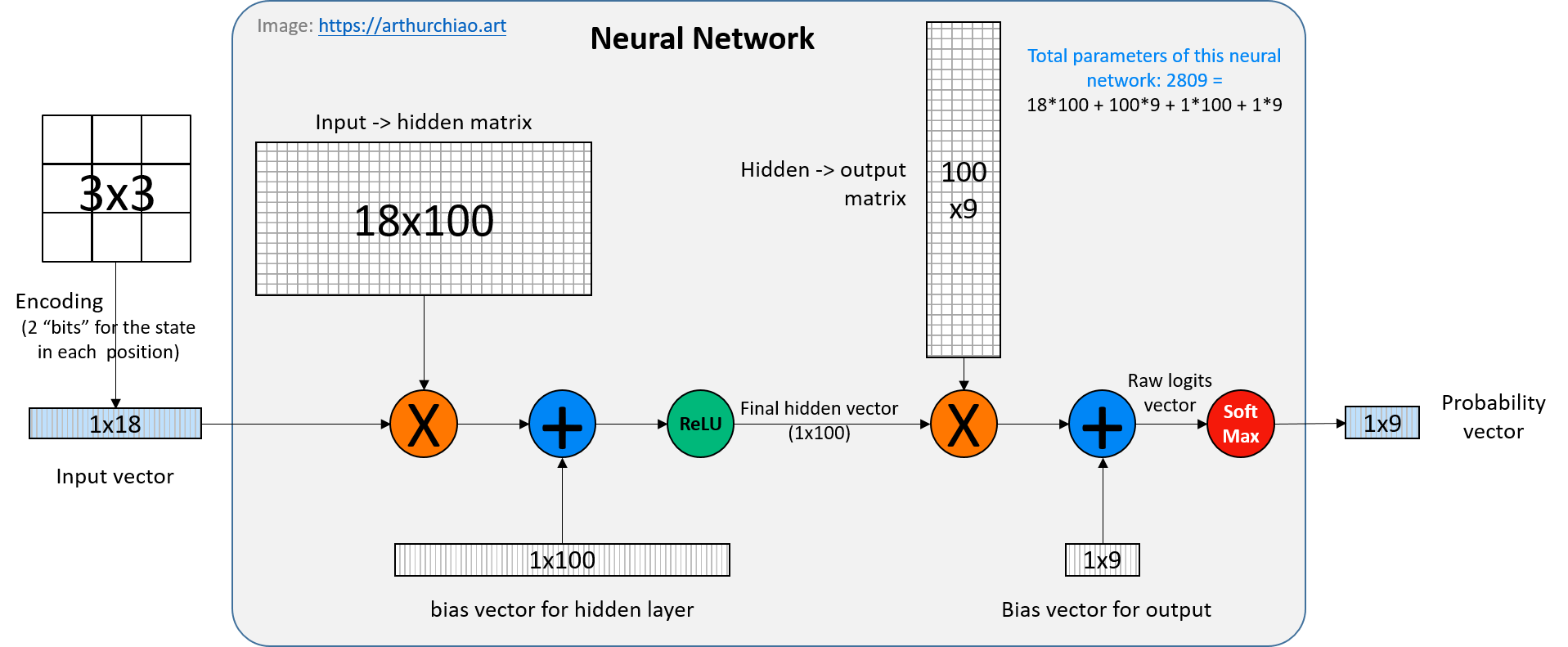
下图就是本文用来训练下井字棋的神经网络,

Fig. A simple neural network for reinforcement learning in this post
对于非科班的人来说,“神经网络”这个词听起来很神秘,但实际上如图所示,神经网络就是一些简单的数学运算, 以上神经网络的处理过程可以归纳为:
- 两次矩阵乘法
- 两次矩阵(向量)加法
-
两次激活(ReLU 和 softmax)。
- 激活函数(activation function)这个名字听起来有点玄乎,其实就是一些对输入进行非线性压缩的简单数学函数,
例如输入的范围可能是正负无穷,经过某个激活函数的变换,输出的范围可能就是
0.0~1.0了。 激活函数也叫非线性函数,这是相对于前面的矩阵运算而言的,因为矩阵运算都是线性的。 - ReLU 和 softmax 这俩函数也是本文自己实现的,包括在了 400 行代码里,
ReLU是将输入向量中小于零的元素截断为零;softmax是将一组“浮点数表示的可能性大小”(例如范围在正负无穷)转换为0.0~0.1之间的 “概率表示”;
- 激活函数(activation function)这个名字听起来有点玄乎,其实就是一些对输入进行非线性压缩的简单数学函数,
例如输入的范围可能是正负无穷,经过某个激活函数的变换,输出的范围可能就是
1.3 代码说明
本文代码只用了标准库函数,没用其他额外依赖。 原项目的代码是训练完之后直接开始人机对战,相当于训练和推理的代码混在一起了, 为了方便理解这两个过程,本文稍作修改,将这两部分分开了,
- 训练代码
train.c,将训练好的神经网络保存到文件; - 推理代码
play.c,从文件中加载训练好的神经网络,开始人机对战,并且不再继续学习(不再更新神经网络权重,原项目的代码是继续更新)。
这两部分代码都会用到的一些结构体和函数,放在了 common.h。
先上效果,以便有个直观印象。
2.1 编译
$ make
rm -f train play 2>/dev/null
cc train.c common.h -o train -O3 -Wall -W -ffast-math -lm
cc play.c common.h -o play -O3 -Wall -W -ffast-math -lm
2.2 训练
不加参数时,默认是训练 150w 局,实际上 200w 效果就很好了,不用担心速度,非常快!
$ ./train 2000000
Training neural network with 2000000 games
Training neural network against 2000000 random games...
Games: 10000, Wins: 7987 (79.9%), Losses: 1003 (10.0%), Ties: 1010 (10.1%)
Games: 20000, Wins: 8621 (86.2%), Losses: 282 (2.8%), Ties: 1097 (11.0%)
Games: 30000, Wins: 8653 (86.5%), Losses: 219 (2.2%), Ties: 1128 (11.3%)
Games: 40000, Wins: 8720 (87.2%), Losses: 198 (2.0%), Ties: 1082 (10.8%)
...
Games: 1990000, Wins: 8376 (83.8%), Losses: 33 (0.3%), Ties: 1591 (15.9%)
Games: 2000000, Wins: 8409 (84.1%), Losses: 35 (0.3%), Ties: 1556 (15.6%)
Training complete!
Neural network saved to ttt_nn.bin
注意,由于神经网络的权重是完全随机初始化的,所以每次训练的结果会有一些差异,但总体来说,效果都是很好的。
查看生成的神经网络文件大小:
$ ll ttt_nn.bin
11K ttt_nn.bin
2.3 人机对战(推理)
$ ./play
Neural network loaded from ttt_nn.bin
Ready to play! You are X, the computer is O.
Welcome to Tic Tac Toe! You are X, the computer is O.
Enter positions as numbers from 0 to 8 (see picture).
... 012
... 345
... 678
Your move (0-8):
比如想在最中间下子,就输入 4,
Your move (0-8): 4
... 012
.X. 345
... 678
Computer\'s move:
Neural network move probabilities:
0.0% 0.0% 0.0%
0.0% 0.0% 0.0%
100.0%*# 0.0% 0.0%
Sum of all probabilities: 1.00
Computer placed O at position 6
... 012
.X. 345
O.. 678
Your move (0-8):
可以看到神经网络计算认为最优的位置是 6,也就是左下角,然后在这个位置下子。 接下来就又轮到人了,依次进行,直到游戏结束。
2.4 小结
以上已经看到了游戏的效果。接下来我们深入到代码,看看整个 RL 训练过程是如何实现的。
3.1 棋盘状态 struct GameState
// Game board representation.
typedef struct {
char board[9]; // Can be "." (empty) or "X", "O".
int current_player; // 0 for player (X), 1 for computer (O).
} GameState;
棋盘是 3x3 的九宫格,每个格子可以是空、X 或 O。
本文的规则是人先下,电脑后下;人用 “X”,电脑用 “O”。
3.2 神经网络的定义
这个神经网络非常简单:只有一个隐藏层, 足够模拟如此简单的游戏了(添加更多层不会加快收敛速度,也不会玩得更好)。
3.2.1 struct NeuralNetwork
/* Neural network structure. For simplicity we have just one hidden layer and fixed sizes.
* However for this problem going deeper than one hidden layer is useless. */
typedef struct {
// Weights and biases.
float weights_ih[NN_INPUT_SIZE * NN_HIDDEN_SIZE];
float weights_ho[NN_HIDDEN_SIZE * NN_OUTPUT_SIZE];
float biases_h[NN_HIDDEN_SIZE];
float biases_o[NN_OUTPUT_SIZE];
// Activations are part of the structure itself for simplicity.
float inputs[NN_INPUT_SIZE];
float hidden[NN_HIDDEN_SIZE];
float raw_logits[NN_OUTPUT_SIZE]; // Outputs before softmax().
float outputs[NN_OUTPUT_SIZE]; // Outputs after softmax().
} NeuralNetwork;
注意,只有前面四个变量(两个权重矩阵,两个 bias 向量)是神经网络的参数, 后面三个变量是为了计算方便,也放到了神经网络结构体里。
Activations are always memorized directly inside the neural network, so calculating the deltas and performing the backpropagation is very simple.
我们神经网络的具体参数定义:
// Neural network parameters.
#define NN_INPUT_SIZE 18 // 这个大小跟棋盘状态的编码方式有关,后面会讲到。
#define NN_HIDDEN_SIZE 100
#define NN_OUTPUT_SIZE 9
对应的就是前面已经展示过的图:

Fig. A simple neural network for reinforcement learning in this post
3.2.2 参数量(模型大小)的计算
注意,井字棋只有 5478 种可能的状态,而根据这些参数和前面的结构体定义,
我们的神经网络的参数总数是 2809,
18 (inputs) * 100 (hidden) +
100 (hidden) * 9 (outputs) weights +
100 + 9 biases
= 2809
这意味着我们的神经网络几乎可以记住游戏的每个状态。 你可以将隐藏层的大小降到 25(或更小),这时参数大约是 700 左右,它仍然能够很好地玩(但肯定会差一些)。
3.3 将棋盘状态转换为神经网络输入:board_to_inputs
棋盘每个位置的状态共三种:
- 空白:
. - 玩家已经下子:
X - 电脑已经下子:
O
所以这里用了一个(逻辑意义上的)2bit 编码方式,将以上状态分别编码为 00、10、01,作为神经网络的输入。

Fig. A simple neural network for reinforcement learning in this post
/* Convert board state to neural network inputs. Note that we use a peculiar encoding I descrived here:
* https://www.youtube.com/watch?v=EXbgUXt8fFU
*
* Instead of one-hot encoding, we can represent N different categories
* as different bit patterns. In this specific case it's trivial:
*
* 00 = empty
* 10 = X
* 01 = O
*
* Two inputs per symbol instead of 3 in this case, but in the general case
* this reduces the input dimensionality A LOT.
*
* LEARNING OPPORTUNITY: You may want to learn (if not already aware) of
* different ways to represent non scalar inputs in neural networks:
* One hot encoding, learned embeddings, and even if it's just my random
* exeriment this "permutation coding" that I'm using here.
*/
static void board_to_inputs(GameState *state, float *inputs) {
for (int i = 0; i < 9; i++) {
if (state->board[i] == '.') {
inputs[i*2] = 0;
inputs[i*2+1] = 0;
} else if (state->board[i] == 'X') {
inputs[i*2] = 1;
inputs[i*2+1] = 0;
} else { // 'O'
inputs[i*2] = 0;
inputs[i*2+1] = 1;
}
}
}
由于棋盘是一个 3x3 的矩阵,所以输入向量的长度是 2*9=18。
这也是前面看到的 NN_INPUT_SIZE 定义的由来:
3.4 前向传播 forward_pass

Fig. A simple neural network for reinforcement learning in this post
前向传播过程实现的就是图中的 neural network 部分,
/* Get the best move for the computer using the neural network.
* Neural network foward pass (inference). We store the activations
* so we can also do backpropagation later. */
static void forward_pass(NeuralNetwork *nn, float *inputs) {
memcpy(nn->inputs, inputs, NN_INPUT_SIZE * sizeof(float));
// Input to hidden layer.
for (int i = 0; i < NN_HIDDEN_SIZE; i++) {
float sum = nn->biases_h[i];
for (int j = 0; j < NN_INPUT_SIZE; j++) {
sum += inputs[j] * nn->weights_ih[j * NN_HIDDEN_SIZE + i];
}
nn->hidden[i] = relu(sum);
}
// Hidden to output (raw logits).
for (int i = 0; i < NN_OUTPUT_SIZE; i++) {
nn->raw_logits[i] = nn->biases_o[i];
for (int j = 0; j < NN_HIDDEN_SIZE; j++) {
nn->raw_logits[i] += nn->hidden[j] * nn->weights_ho[j * NN_OUTPUT_SIZE + i];
}
}
// Apply softmax to get the final probabilities.
softmax(nn->raw_logits, nn->outputs, NN_OUTPUT_SIZE);
}
3.4.1 计算过程

Fig. A simple neural network for reinforcement learning in this post
可以分为两个过程:
- 左边:一次矩阵乘法 + 一次矩阵加法 + 一次激活函数(ReLU)
- 输入:1x18 的 input vector,是当前棋盘状态的编码;
- 输出:1x100 的 hidden vector;
- 右边:一次矩阵乘法 + 一次矩阵加法 + 一次激活函数(softmax)
- 输入:1x100 的 hidden vector;
- 输出:1x9 的 output vector,其中的每个元素表示在对应位置下子的概率。
接下来再详细看看两个激活函数。
3.4.2 非线性/激活函数 relu
ReLU 就一行代码,将输入 <0 的部分截断为 0:
/* ReLU activation function */
static float relu(float x) {
return x > 0 ? x : 0;
}
神经网络的每个参数模拟的是大脑的一个神经元,对应到 ReLU,这里的直观的解释是, 如果刺激强度太弱,那么相应的神经元是不会被激活的,或者说刺激强度超过一个阈值,神经元才会被激活。
使用 RELU 是因为它很简单,并且能适用于几乎所有场景。 权重初始化跟 RELU 没任何关系,只完全随机的。
3.4.3 非线性/激活函数 softmax
softmax 跟模拟大脑和神经元就没有关系了,是个纯数学技巧,
用来将一组(通常是正负无穷范围内的)数值转换为概率分布。
直观上也很好理解:
- 如果原始输入
x是正负无穷范围内的数值,那 ex 的范围就是 0 到正无穷; - 对所有
x都计算 ex,再取加权,就得到了一个总和为100%的 概率分布。
Fig. A definition of softmax. Image Source: wikipedia
实际上会有各种变种,但基本原理都是这样。详见 wikipedia softmax function。
/* Apply softmax activation function to an array input, and
* set the result into output. */
static void softmax(float *input, float *output, int size) {
/* Find maximum value then subtact it to avoid numerical stability issues with exp(). */
float max_val = input[0];
for (int i = 1; i < size; i++) {
if (input[i] > max_val) {
max_val = input[i];
}
}
// Calculate exp(x_i - max) for each element and sum.
float sum = 0.0f;
for (int i = 0; i < size; i++) {
output[i] = expf(input[i] - max_val);
sum += output[i];
}
// Normalize to get probabilities.
if (sum > 0) {
for (int i = 0; i < size; i++) {
output[i] /= sum;
}
} else {
/* Fallback in case of numerical issues, just provide a uniform distribution. */
for (int i = 0; i < size; i++) {
output[i] = 1.0f / size;
}
}
}
softmax() 得到的输出就是一个 1x9 的概率向量,其中的每个值表示的是“下一步在这个位置下子的概率”。
In theory we use cross entropy to calculate the loss function, but in practice we evaluate our agent based on the results of the games, so we only use it implicitly here:
deltas[i] = output[i] - target[i]That is the delta in case of softmax and cross entropy.
3.5 神经网络计算下一步最优 get_computer_move
这个函数的目的是寻找神经网络输出(1x9)中,目前仍然空白(未下子)且概率最大的位置,
返回的 best_move 就是这个位置,意思是去这个位置下子。
3.5.1 调用栈
get_computer_move
|- board_to_inputs
|- forward_pass
|- for (i=0; i<9; i++)
| if (state->board[i] == '.' && (best_move == -1 || nn->outputs[i] > best_legal_prob)) {
| best_move = i;
| best_legal_prob = nn->outputs[i];
| }
|- return best_move
3.5.2 代码
为避免干扰,这里 Debug 相关的代码去掉了,只保留核心代码:
/* Get the best move for the computer using the neural network.
* Note that there is no complex sampling at all, we just get
* the output with the highest value THAT has an empty tile. */
static int get_computer_move(GameState *state, NeuralNetwork *nn, int display_probs) {
float inputs[NN_INPUT_SIZE];
board_to_inputs(state, inputs);
forward_pass(nn, inputs); // 得到了下一步的概率分布,保存在 nn->outputs[] 中
int best_move = -1;
float best_legal_prob = -1.0f;
for (int i = 0; i < 9; i++) {
if (state->board[i] == '.' && (best_move == -1 || nn->outputs[i] > best_legal_prob)) {
best_move = i;
best_legal_prob = nn->outputs[i];
}
}
return best_move;
}
3.6 小结
以上就是训练和推理都会用到的一些结构体和函数。 接下来看看具体的训练过程。
4.1 main 函数
步骤:
- 初始化神经网络。
- 训练神经网络,让它与一个每次随机下子的对手对弈 N 局。
- 保存训练好的神经网络。
4.1.1 代码
int main(int argc, char **argv) {
int random_games = 150000; // Fast and enough to play in a decent way.
const char *output_file = "ttt_nn.bin";
if (argc > 1) random_games = atoi(argv[1]);
if (argc > 2) output_file = argv[2];
srand(time(NULL));
// Initialize neural network.
NeuralNetwork nn;
init_neural_network(&nn);
printf("Training neural network with %d games\n", random_games);
// Train against random moves.
if (random_games > 0) train_against_random(&nn, random_games);
// Save the trained neural network
save_neural_network(&nn, output_file);
return 0;
}
4.1.2 调用栈
main
|- init_neural_network
|- train_against_random
| |- for (i=0; i<num_games; i++)
| play_random_game
| |- init_game
| |- while (!check_game_over(&state, &winner)) {
| | if (state.current_player == 0) // Random player's turn (X)
| | move = get_random_move(&state);
| | else // Neural network's turn (O)
| | move = get_computer_move(&state, nn, 0);
| | char symbol = (state.current_player == 0) ? 'X' : 'O';
| | state.board[move] = symbol;
| | move_history[(*num_moves)++] = move;
| | state.current_player = !state.current_player;
| |- learn_from_game
| |- backprop
|- save_neural_network
4.2 init_neural_network 函数
/* Initialize a neural network with random weights, we should
* use something like He weights since we use RELU, but we don't care as this is a trivial example. */
#define RANDOM_WEIGHT() (((float)rand() / RAND_MAX) - 0.5f)
void init_neural_network(NeuralNetwork *nn) {
// Initialize weights with random values between -0.5 and 0.5
for (int i = 0; i < NN_INPUT_SIZE * NN_HIDDEN_SIZE; i++)
nn->weights_ih[i] = RANDOM_WEIGHT();
for (int i = 0; i < NN_HIDDEN_SIZE * NN_OUTPUT_SIZE; i++)
nn->weights_ho[i] = RANDOM_WEIGHT();
for (int i = 0; i < NN_HIDDEN_SIZE; i++)
nn->biases_h[i] = RANDOM_WEIGHT();
for (int i = 0; i < NN_OUTPUT_SIZE; i++)
nn->biases_o[i] = RANDOM_WEIGHT();
}
4.3 train_against_random -> for {play_random_game}
/* Train the neural network against random moves. */
void train_against_random(NeuralNetwork *nn, int num_games) {
int move_history[9];
int wins = 0, losses = 0, ties = 0;
printf("Training neural network against %d random games...\n", num_games);
int played_games = 0;
for (int i = 0; i < num_games; i++) {
char winner = play_random_game(nn, move_history);
}
printf("\nTraining complete!\n");
}
4.4 play_random_game
这里是训练过程的核心代码,play_random_game 让 computer 和 random 对手下棋,
- computer 用神经网络(feed forward)计算下一步最优位置。
- random 对手随机下子。
一局结束之后,根据游戏结果进行奖励(强化学习)。
/* Play a game against random moves and learn from it.
*
* This is a very simple Montecarlo Method applied to reinforcement learning:
*
* 1. We play a complete random game (episode).
* 2. We determine the reward based on the outcome of the game.
* 3. We update the neural network in order to maximize future rewards.
*
* LEARNING OPPORTUNITY: while the code uses some Montecarlo-alike
* technique, important results were recently obtained using
* Montecarlo Tree Search (MCTS), where a tree structure repesents
* potential future game states that are explored according to
* some selection: you may want to learn about it. */
char play_random_game(NeuralNetwork *nn, int *move_history) {
GameState state;
char winner = 0;
int num_moves = 0;
init_game(&state);
while (!check_game_over(&state, &winner)) {
int move;
if (state.current_player == 0) { // Random player's turn (X)
move = get_random_move(&state);
} else { // Neural network's turn (O)
move = get_computer_move(&state, nn, 0);
}
/* Make the move and store it: we need the moves sequence during the learning stage. */
char symbol = (state.current_player == 0) ? 'X' : 'O';
state.board[move] = symbol;
move_history[num_moves++] = move;
// Switch player.
state.current_player = !state.current_player;
}
// Learn from this game - neural network is 'O' (even-numbered moves).
learn_from_game(nn, move_history, num_moves, 1, winner);
return winner;
}
/* Get a random valid move, this is used for training against a random opponent.
* Note: this function will loop forever if the board is full, but here we want simple code. */
int get_random_move(GameState *state) {
while(1) {
int move = rand() % 9;
if (state->board[move] != '.') continue;
return move;
}
}
4.4.1 和随机下子的对手下一局
记录双方的每一步保存在 move_history 中,
while (!check_game_over(&state, &winner)) {
int move;
if (state.current_player == 0) { // Random player's turn (X)
move = get_random_move(&state);
} else { // Neural network's turn (O)
move = get_computer_move(&state, nn, 0);
}
/* Make the move and store it: we need the moves sequence during the learning stage. */
char symbol = (state.current_player == 0) ? 'X' : 'O';
state.board[move] = symbol;
move_history[num_moves++] = move;
// Switch player.
state.current_player = !state.current_player;
}
4.5 learn_from_game
根据这一局的结果,对神经网络进行奖励(强化学习)。
// Learn from this game - neural network is 'O' (even-numbered moves).
learn_from_game(nn, move_history, num_moves, 1, winner);
五个参数:
- nn:神经网络;
- move_history:记录了整局游戏的每一步;
- num_moves:整局游戏的步数;
1:表示游戏中的偶数步骤是神经网络下的;- winner:赢家是谁。
4.5.1 强化学习的奖励策略
使用的 reward policy: 基于奖励,在神经网络计算下一步时,我们列出所有可能的下一个状态,并奖励每个状态获胜的 move (不仅仅是最终获胜的那一步,而是赢了的这一局中,所有执行的步骤),
- 赢:要奖励的 move 为 1(100%),将所有其他 move 为 0。
- 平:也给予奖励,但是比胜利的奖励要小。
- 负:target move 奖励为 0,非法 moves 奖励也为 0,其他合法 moves 奖励为
1/(number-of-valid-moves)。
此外,我们还根据游戏的进度进行缩放:
float move_importance = 0.5f + 0.5f * (float)move_idx/(float)num_moves;
float scaled_reward = reward * move_importance;
- 游戏前期的 moves,给予较小的奖励,
- 游戏后期(接近游戏结束)的 moves,给予更大的奖励:
Note that the above makes a lot of difference in the way the program works. Also note that while this may seem similar to Time Difference in reinforcement learning, it is not: we don’t have a simple way in this case to evaluate if a single step provided a positive or negative reward: we need to wait for each game to finish. The temporal scaling above is just a way to code inside the network that early moves are more open, while, as the game goes on, we need to play more selectively.
4.5.2 代码
/* Train the neural network based on game outcome.
*
* The move_history is just an integer array with the index of all the moves. */
void learn_from_game(NeuralNetwork *nn, int *move_history, int num_moves, int nn_moves_even, char winner) {
float reward;
char nn_symbol = nn_moves_even ? 'O' : 'X';
if (winner == 'T') {
reward = 0.3f; // Small reward for draw
} else if (winner == nn_symbol) {
reward = 1.0f; // Large reward for win
} else {
reward = -2.0f; // Negative reward for loss
}
GameState state;
float target_probs[NN_OUTPUT_SIZE];
// Process each move the neural network made.
for (int move_idx = 0; move_idx < num_moves; move_idx++) {
// Skip if this wasn't a move by the neural network.
if ((nn_moves_even && move_idx % 2 != 1) || (!nn_moves_even && move_idx % 2 != 0)) {
continue;
}
// Recreate board state BEFORE this move was made.
init_game(&state);
for (int i = 0; i < move_idx; i++) {
char symbol = (i % 2 == 0) ? 'X' : 'O';
state.board[move_history[i]] = symbol;
}
// Convert board to inputs and do forward pass.
float inputs[NN_INPUT_SIZE];
board_to_inputs(&state, inputs);
forward_pass(nn, inputs);
/* The move that was actually made by the NN, that is the one we want to reward (positively or negatively). */
int move = move_history[move_idx];
/* Here we can't really implement temporal difference in the strict
* reinforcement learning sense, since we don't have an easy way to
* evaluate if the current situation is better or worse than the previous state in the game.
*
* However "time related" we do something that is very effective in
* this case: we scale the reward according to the move time, so that
* later moves are more impacted (the game is less open to different solutions as we go forward).
*
* We give a fixed 0.5 importance to all the moves plus a 0.5 that depends on the move position.
* NOTE: this makes A LOT of difference. Experiment with different values.
*
* LEARNING OPPORTUNITY: Temporal Difference in Reinforcement Learning
* is a very important result, that was worth the Turing Award in
* 2024 to Sutton and Barto. You may want to read about it. */
float move_importance = 0.5f + 0.5f * (float)move_idx/(float)num_moves;
float scaled_reward = reward * move_importance;
/* Create target probability distribution: let's start with the logits all set to 0. */
for (int i = 0; i < NN_OUTPUT_SIZE; i++)
target_probs[i] = 0;
/* Set the target for the chosen move based on reward: */
if (scaled_reward >= 0) {
/* For positive reward, set probability of the chosen move to 1, with all the rest set to 0. */
target_probs[move] = 1;
} else {
/* For negative reward, distribute probability to OTHER valid moves,
* which is conceptually the same as discouraging the move that we want to discourage. */
int valid_moves_left = 9-move_idx-1;
float other_prob = 1.0f / valid_moves_left;
for (int i = 0; i < 9; i++) {
if (state.board[i] == '.' && i != move) {
target_probs[i] = other_prob;
}
}
}
/* Call the generic backpropagation function, using our target logits as target. */
backprop(nn, target_probs, LEARNING_RATE, scaled_reward);
}
}
4.5.3 奖励过程:回放每一步,根据真实 input 预测这一步的输出,和真实的输出比较,进行奖励
循环:遍历整局游戏的每一步 move_idx;针对从开始到 move_idx 为止,
- 用实际的状态填充棋盘
0~move_idx-1; - 将 step 1 的状态作为输入,用神经网络预测下一步,得到一个概率分布;
- 进行奖励:根据真实的下一步
move构建目标概率分布target_probs(一个位置是 100%,其他地方都是 0%); - 根据 step 2 & 3 的两个概率分布,调用
backprop函数进行反向传播,更新神经网络的权重。
举个例子,下图这一局只用了总共 5 步 O 方就赢了,右侧是回放到第 3 步(对应到代码是 move_idx=2)时的状态:

Fig. Reward illustration
对照右侧图,对应的奖励过程:
- 将已经回放到的部分作为输入,计算下一步的概率;
- 进行奖励:将真实的下一步作为目标概率分布(
index=8处为 100%,其他位置都是 0%); - 用 step 1 & 2 的两个概率分布进行反向传播,更新神经网络的权重。
4.6 反向传播 backprop
这里使用了很简单的反向传播,代码非常清晰,它的工作方式与监督学习非常相似, 唯一的区别是输入/输出对事先不知道,而是根据强化学习的奖励策略实时提供奖励的。
/* Derivative of ReLU activation function */
float relu_derivative(float x) {
return x > 0 ? 1.0f : 0.0f;
}
/* Backpropagation function.
* The only difference here from vanilla backprop is that we have
* a 'reward_scaling' argument that makes the output error more/less
* dramatic, so that we can adjust the weights proportionally to the reward we want to provide. */
void backprop(NeuralNetwork *nn, float *target_probs, float learning_rate, float reward_scaling) {
float output_deltas[NN_OUTPUT_SIZE];
float hidden_deltas[NN_HIDDEN_SIZE];
/* === STEP 1: Compute deltas === */
/* Calculate output layer deltas:
* Note what's going on here: we are technically using softmax as output function and cross entropy as loss,
* but we never use cross entropy in practice since we check the progresses in terms of winning the game.
*
* Still calculating the deltas in the output as: output[i] - target[i]
* Is exactly what happens if you derivate the deltas with softmax and cross entropy.
*
* LEARNING OPPORTUNITY: This is a well established and fundamental result in neural networks, you may want to read more about it. */
for (int i = 0; i < NN_OUTPUT_SIZE; i++)
output_deltas[i] = (nn->outputs[i] - target_probs[i]) * fabsf(reward_scaling);
// Backpropagate error to hidden layer.
for (int i = 0; i < NN_HIDDEN_SIZE; i++) {
float error = 0;
for (int j = 0; j < NN_OUTPUT_SIZE; j++) {
error += output_deltas[j] * nn->weights_ho[i * NN_OUTPUT_SIZE + j];
}
hidden_deltas[i] = error * relu_derivative(nn->hidden[i]);
}
/* === STEP 2: Weights updating === */
// Output layer weights and biases.
for (int i = 0; i < NN_HIDDEN_SIZE; i++)
for (int j = 0; j < NN_OUTPUT_SIZE; j++)
nn->weights_ho[i * NN_OUTPUT_SIZE + j] -= learning_rate * output_deltas[j] * nn->hidden[i];
for (int j = 0; j < NN_OUTPUT_SIZE; j++)
nn->biases_o[j] -= learning_rate * output_deltas[j];
// Hidden layer weights and biases.
for (int i = 0; i < NN_INPUT_SIZE; i++)
for (int j = 0; j < NN_HIDDEN_SIZE; j++)
nn->weights_ih[i * NN_HIDDEN_SIZE + j] -= learning_rate * hidden_deltas[j] * nn->inputs[i];
for (int j = 0; j < NN_HIDDEN_SIZE; j++)
nn->biases_h[j] -= learning_rate * hidden_deltas[j];
}
分为两步,
- 分别计算 output_deltas 和 hidden_deltas,
- 用以上两个 delta 更新 input-hidden 和 hidden-output 两个矩阵的权重。
4.6.1 output 概率和 target 概率的 delta 计算

Fig. Reward illustration
output_deltas (1x9):
- softmax 得到的概率分布(
nn->outputs)和根据奖励模型得到的目标概率分布(target_probs)之间的 delta vector; - 这里还引入了一个缩放系数
reward_scaling来调整奖励的大小,使结果更好;
4.6.2 hidden layer 的 delta 计算
这一步是将 output layer 的 delta 反向传播到 hidden layer,得到的是 hidden_deltas (1x100):
hidden-output 矩阵(100x9)和 output_deltas(1x9)做矩阵乘法,得到一个 hidden layer 的 delta vector(1x100);
4.6.3 更新神经网络的权重(with learning rate)

Fig. A simple neural network for reinforcement learning in this post
根据设置的学习率 learning_rate,更新神经网络的权重:
| hidden-output matrix | output bias | input-hidden matrix | hidden bias | |
|---|---|---|---|---|
| 大小 | 100x9 | 1x9 | 18x100 | 1x100 |
| 依赖 1 | output_deltas |
output_deltas |
hidden_deltas |
hidden_deltas |
| 依赖 2 | nn->hidden |
- | nn->inputs |
- |
| 公式 | nn->weights_ho[i][j] -= lr * output_deltas[j] * nn->hidden[i] |
nn->biases_o[j] -= lr * output_deltas[j] |
nn->weights_ih[i][j] -= lr * hidden_deltas[j] * nn->inputs[i] |
nn->biases_h[j] -= lr * hidden_deltas[j] |
4.7 save_neural_network
写到文件,在概念上类似于现在的大模型文件,
/* Save neural network parameters to a file */
void save_neural_network(NeuralNetwork *nn, const char *filename) {
FILE *file = fopen(filename, "wb");
if (file == NULL) {
printf("Error opening file for writing: %s\n", filename);
return;
}
// Write weights and biases
fwrite(nn->weights_ih, sizeof(float), NN_INPUT_SIZE * NN_HIDDEN_SIZE, file);
fwrite(nn->weights_ho, sizeof(float), NN_HIDDEN_SIZE * NN_OUTPUT_SIZE, file);
fwrite(nn->biases_h, sizeof(float), NN_HIDDEN_SIZE, file);
fwrite(nn->biases_o, sizeof(float), NN_OUTPUT_SIZE, file);
fclose(file);
printf("Neural network saved to %s\n", filename);
}
非常简单,从文件中加载神经网络参数,然后开始游戏,类似于现在的加载大模型开始提供推理服务,
/* Load neural network parameters from a file */
int load_neural_network(NeuralNetwork *nn, const char *filename) {
FILE *file = fopen(filename, "rb");
if (file == NULL) {
printf("Error opening file for reading: %s\n", filename);
return 1;
}
// Read weights and biases
size_t items_read = 0;
items_read += fread(nn->weights_ih, sizeof(float), NN_INPUT_SIZE * NN_HIDDEN_SIZE, file);
items_read += fread(nn->weights_ho, sizeof(float), NN_HIDDEN_SIZE * NN_OUTPUT_SIZE, file);
items_read += fread(nn->biases_h, sizeof(float), NN_HIDDEN_SIZE, file);
items_read += fread(nn->biases_o, sizeof(float), NN_OUTPUT_SIZE, file);
fclose(file);
// Check if we read the expected number of items
size_t expected_items = NN_INPUT_SIZE * NN_HIDDEN_SIZE +
NN_HIDDEN_SIZE * NN_OUTPUT_SIZE +
NN_HIDDEN_SIZE +
NN_OUTPUT_SIZE;
if (items_read != expected_items) {
printf("Error: Read %zu items, expected %zu\n", items_read, expected_items);
return 2;
}
printf("Neural network loaded from %s\n", filename);
return 0;
}
int main(int argc, char **argv) {
const char *input_file = "ttt_nn.bin";
if (argc > 1) input_file = argv[1];
// Load neural network from file
NeuralNetwork nn;
if (load_neural_network(&nn, input_file)) {
printf("Failed to load neural network.\n");
return 1;
}
printf("Ready to play! You are X, the computer is O.\n");
// Play game with human
while(1) {
char play_again;
play_game(&nn);
printf("Play again? (y/n): ");
scanf(" %c", &play_again);
if (play_again != 'y' && play_again != 'Y') break;
}
return 0;
}
原作者的课后作业,供学有余力的同学参考:
- Can this approach work with connect four as well? The much larger space of the problem would be really interesting and less of a toy.
- Train the network to play both sides by having an additional input set, that is the symbol that is going to do the move (useful especially in the case of connect four) so that we can use the network itself as opponent, instead of playing against random moves.
- Implement proper sampling, in the case above, so that initially moves are quite random, later they start to pick more consistently the predicted move.
- MCTS.
如有侵权请联系:admin#unsafe.sh


