2025-1-3 15:38:34 Author: securityboulevard.com(查看原文) 阅读量:0 收藏

Some of our astute readers noticed an apparent anomaly in the graph comparing the complexities of Shor’s algorithm and GNFS in the original blog. Specifically, it seemed as though GNFS (General Number Field Sieve) outperformed quantum-accelerated Shor’s algorithm for practical RSA key sizes (e.g., 2048 bits). This led to the seemingly absurd conclusion that RSA could be broken using classical computers and GNFS—a glaring error on my part.
In this clarification, I’ll unpack the simplifying assumptions I made, explain how they introduced this error, and provide an improved approximation that yields more accurate insights.
The Simplifying Assumptions
Although my initial goal was not strict accuracy, my oversimplifications distorted the results, rendering the graph incorrect.
GNFS Complexity
The actual complexity of GNFS, as described on Wikipedia, is:
exp (((64/9)1/3 +o(1)) × (log N)1/3 × (log (log N))2/3))
Where N is the number being factorized
The true complexity of GNFS depends on various factors, such as:
- Polynomial selection
- Solving large linear systems/matrices
- Distributed computing resources
We can also express this in terms of Bits b required to represent the number N
2b ~ N, Or b = log2N
To simplify, I approximated GNFS complexity using only the bit size:
- First Simplification: Ignore constants:
exp (b1/3 × (log b)2/3)
- Second Simplification: Focus on the primary dependency and ignore and secondary dependencies since it grows slowly:
e ^ (b1/3)
While convenient for plotting, these simplifications underestimated GNFS’s complexity, particularly for smaller bit sizes. For example:
| b (bit size) | b3 | e^(b1/3) |
|---|---|---|
| 1 | 1 | 2.72 |
| 8 | 512 | 7.39 |
| 4096 | 6.87×109 | 8.88×106 |
| 32768 | 3.52×1013 | 7.90×1013 |
Clearly, e^(b1/3) appears much smaller than b3 for smaller bit sizes, leading to the mistaken impression that GNFS was far more efficient than it truly is.
Key Length vs. Bit Strength
In cryptography, understanding the distinction between key length and bit strength is crucial
Key Length
The key length is the size of the cryptographic key, expressed in bits:
- RSA-2048: 2048-bit key
- RSA-4096: 4096-bit key
- AES-128: 128-bit key
If an attack involved brute-forcing all possible keys, it would require 2key length attempts.
Bit Strength
Bit strength reflects the computational effort required to break a cryptographic algorithm
- RSA-2048: Key length = 2048 bits, Bit strength ≈ 112 bits
- RSA-4096: Key length = 4096 bits, Bit strength ≈ 140 bits
- AES-128: Key length = 128 bits, Bit strength ≈ 128 bits
Since RSA relies on factorization, attackers only need to factorize the 2048-bit modulus to break RSA-2048, requiring 2112 steps (not 22048) using GNFS. A practical quantum computer running Shor’s algorithm could reduce this to O(20483) or roughly 233, dramatically lowering RSA-2048’s effective bit strength to just 33.
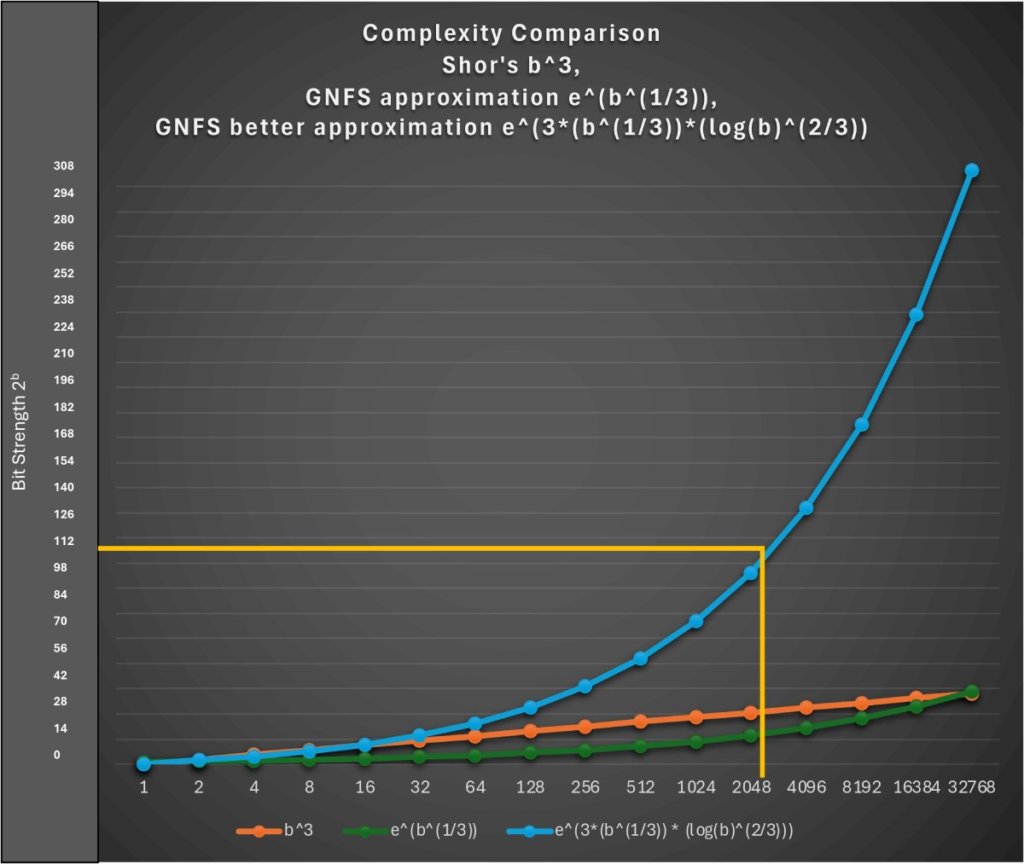
Improved Approximation and Graph
To better represent the complexity, I revised my assumptions as follows:
- Use bit strength (Y-axis) against key length (X-axis) in the graph.
- Replace e^(b1/3) with:
e ^ (3 × b1/3 × (log b)2/3)
Here, 3 approximates (64/9)1/3 + o(1), aligning better with known bit strength values.
For instance:
| b (bit size) | b3 | e^(b1/3) | e ^ (3 × b1/3 × (log b)2/3) |
|---|---|---|---|
| 1 | 1, 20 | 2.72, 21.44 | 1, 20 |
| 8 | 512, 29 | 7.39, 22.89 | 272, 28.09 |
| 4096 | 6.87×109, 236 | 8.88×106, 223 | 1.20×1049, 2163 |
| 32768 | 3.52×1013, 245 | 7.90×1013, 246 | 7.94×10113, 2378 |
Acknowledgements and Gratitude
I sincerely appreciate the insightful feedback from readers, which prompted this deeper dive into GNFS and Shor’s algorithm complexities. It’s my hope that this clarification makes the fascinating math behind quantum computing more accessible. If you’re comfortable with me publicly acknowledging your contributions, let me know, and I’ll happily update this post.
Thank you again for helping me improve this analysis!
The post Clarification on Shor’s Algorithm and GNFS Comparison appeared first on ColorTokens.
*** This is a Security Bloggers Network syndicated blog from ColorTokens authored by Satyam Tyagi. Read the original post at: https://colortokens.com/blogs/quantum-computing-cybersecurity-shors-algorithm-gnfs-rsa-encryption/
如有侵权请联系:admin#unsafe.sh